改进的FCM半监督聚类算法

郭新辰, 樊秀玲, 郗仙田, 韩 啸

(1.东北电力大学 理学院, 吉林 吉林 132012; 2.吉林大学 学报编辑部, 长春 130012)

研究简报

改进的FCM半监督聚类算法

郭新辰1, 樊秀玲1, 郗仙田1, 韩 啸2

(1.东北电力大学 理学院, 吉林 吉林 132012; 2.吉林大学 学报编辑部, 长春 130012)

通过将类间分离度函数引入到模糊C-均值聚类算法中, 结合半监督的思想, 建立基于信息熵的半监督模糊C-均值聚类模型, 并对该模型的求解过程进行推导, 提出一种新的算法.为了验证算法的有效性, 将该算法在UCI数据集上进行实验, 实验结果表明, 该算法比仅引入信息熵的模糊C-均值聚类方法聚类性能更好.

半监督聚类； 模糊C-均值算法； 信息熵

在机器学习问题中, 人们容易获取大量未标签的样本和少量已标签的样本, 若从这些样本中挖掘出潜在的价值信息, 常采用半监督学习方法提高对样本的学习泛化能力.半监督学习方法主要利用有标记数据构造学习机, 并对部分无标记数据进行预测, 再将无标记数据和对应的预测标记加入训练集中, 重新对学习机进行训练, 以提高学习机性能.

半监督学习方法[1]一般分为半监督分类和半监督聚类.二者区别在于半监督聚类能使用标记样本转化成分类, 也能根据需要扩展和修改存在的分类, 以反映数据中的其他规则.模糊聚类算法中应用较典型的是模糊C-均值聚类算法, 简称FCM, 这种方法存在一定的局限性, 即在每次聚类过程中数据均匀收缩.文献[2]通过在标准FCM目标函数的约束条件中增加信息熵约束, 提高了聚类性能, 弥补了模糊聚类存在数据收缩问题的不足, 即常用的引入信息熵模糊C-均值聚类方法, 简称IEFCM, 但该方法未利用部分样本的监督信息; 为了减少有价值信息的浪费, 文献[3-5]结合半监督思想及标记样本隶属度赋值问题, 在FCM算法的数学模型中引进辅助变量加入先验信息以影响聚类.由于实际生产的干扰因素过多且环境多变, 因此获得的数据样本信息通常会包含一些干扰信息； 文献[6]根据FCM的目标函数物理意义, 引进隶属度补偿项和类中心最大项, 通过迭代优化代价函数, 得到了较满意的聚类结果.

本文将引入信息熵的模糊C-均值聚类方法与半监督性质及类间分离度相结合, 提出一种改进的聚类算法, 即基于模糊C-均值的半监督聚类算法, 简称SIEFCM.

1 基于信息熵的模糊C-均值半监督聚类算法

1.1 模糊C-均值聚类算法 FCM算法[7-9]是目前广泛采用的一种聚类算法, 即使对于很难明显分类的变量, 模糊C-均值聚类也能得到较满意的效果.

传统的模糊C-均值聚类是用隶属度确定聚类程度的一种聚类算法, 即把n个d维样本xj(j=1,2,…,n)分为c个组, 每组即为一类, 聚类中心集为{v1,v2,…,vc}, 其中vi为类i的类中心.

标准FCM算法的数学模型为

其中:uij表示样本xj属于类i的程度；U为uij构成的c×N隶属度矩阵；V为vi构成的c×n类中心矩阵；m∈(1,+∞)表示一个加权模糊指数, 反映控制隶属度在各类间共享的程度；dij=‖xj-vi‖表示样本点xj到类中心vi的欧氏距离.

1.2 基于信息熵的FCM聚类算法 约束条件中引入信息熵的FCM算法数学模型为

其等价于优化问题

其中:dkj=‖xj-vk‖表示样本点xj到类中心vk的欧氏距离；η∈(0,1)为类中心影响程度调节因子参数；

其他参数与式(1)定义相同.式(3)与式(1)相比, 显然考虑了数据在每次聚类过程中数据空间上的实际分布特性.

1.3 基于信息熵的模糊C-均值半监督聚类算法 对隶属度引入半监督性质的补偿项Ψ, 描述监督信息, 其表达式为

类间分离度函数Φ描述不同类间的分散度问题, 其表达式为

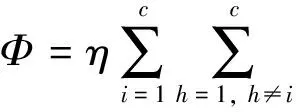
根据式(3)和半监督聚类的定义, 本文希望类间超平面间隔更大.已知信息样本具有引导聚类的能力, 其隶属度值的影响使最终聚类质量尽可能比用随机数聚类的准确性更高.因此, 对式(3)做修改, 对隶属度引入半监督性质的补偿项和类间分离度函数, 得到新的目标函数, 进而得到本文提出的基于模糊C-均值的半监督聚类方法的数学模型, 其表达形式为

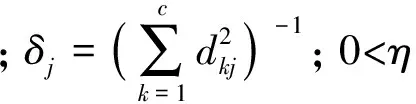
对于模型(6), 利用Lagrange乘数因子法进行求解, 构造Lagrange函数为

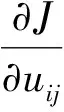
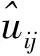
基于信息熵的模糊C-均值半监督聚类算法步骤如下：

1) 初始化隶属度U(t),V(t), 其中t为迭代次数；

2) 将V(t)按式(7)更新为V(t+1)；

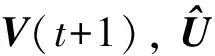
4) 当|J(t+1)-J(t)|<ε, 或迭代次数t超过最大迭代次数M时, 算法终止; 否则转2).

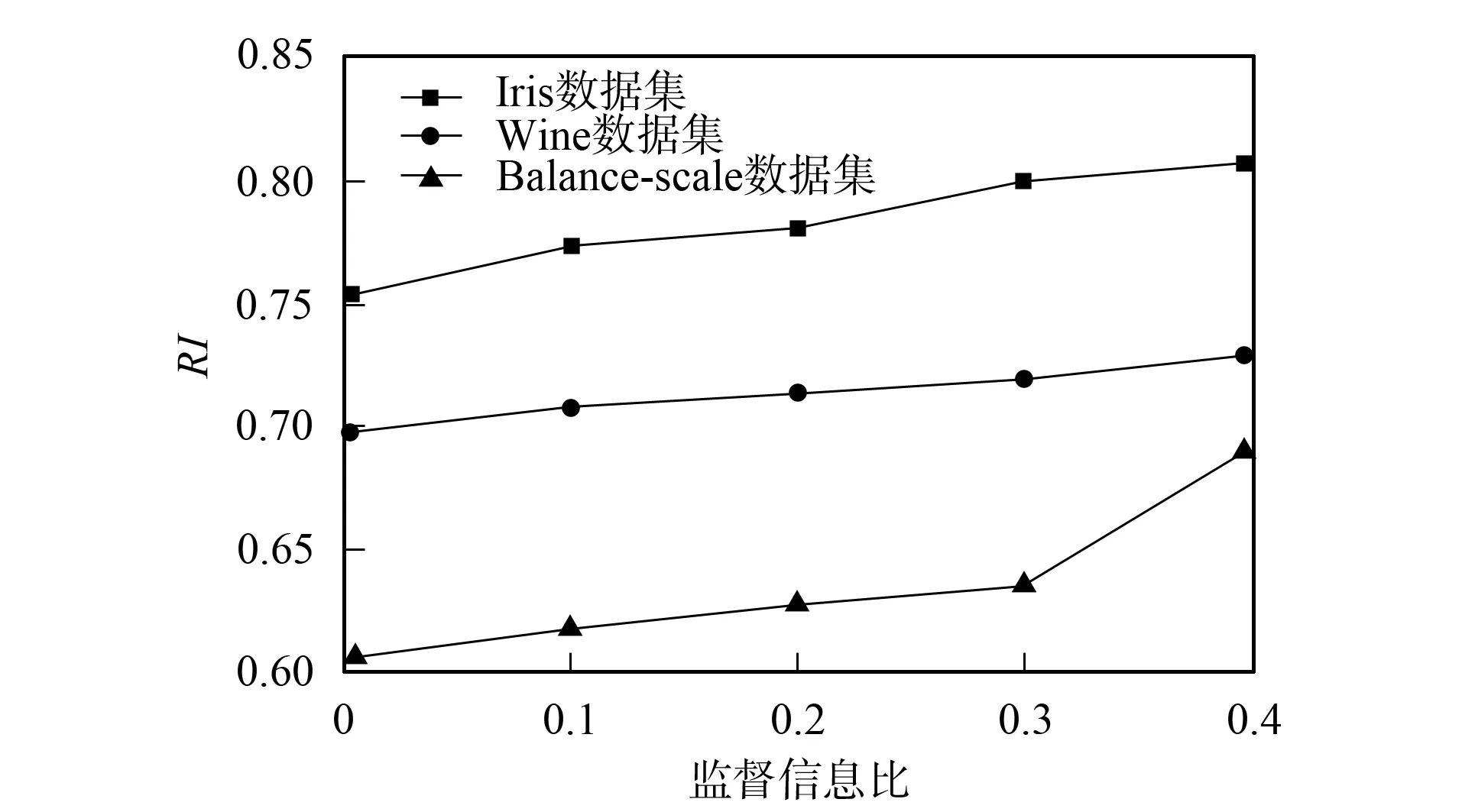
图1 性能指标与监督信息比的变化曲线Fig.1 Curves of performance index vs the weight of supervised information

2 仿真实验

为了验证本文算法的合理性, 在UCI机器学习数据库中, 采用常用于聚类方法检测的Iris数据集、Wine数据集和Balance-scale数据集进行实验, 数据集信息列于表1.

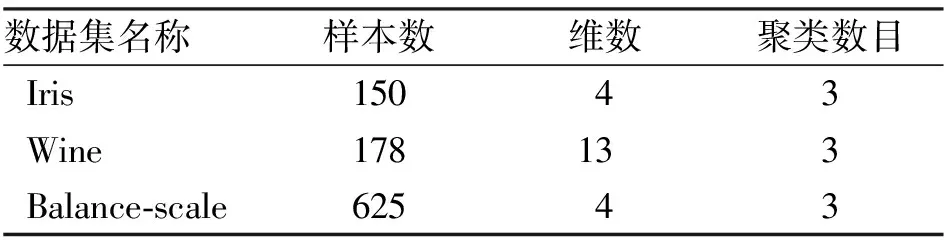
表1 实验数据集信息Table 1 Related information description ofthe experimental data sets

对于每个数据集, 随机选取总体样本的10%,20%,30%,40%作为测试集.为了客观进行不同算法性能的优劣比较, 设参数m=2,η=0.000 1.

性能评价指标为RI=n0/n, 其中n0为测试集的聚类结果与标准数据集对比后得到正确分类样本的平均个数；n为测试数据集的样本总数；RI值越大, 表示聚类准确性越大, 聚类效果越好.重复5次实验, 实验结果RI的平均值列于表2.由表2可见, 随着监督信息的增多, 聚类的正确率有增大趋势, 表明监督信息数据具有指导作用.在Iris数据集、Wine数据集和Balance-scale数据集上性能指标与监督信息比的变化曲线如图1所示.由图1可见： 在不同数据集上,RI值随监督信息比值的增大而增大； 虽然聚类正确率的上升速度不能按监督信息量的增幅而变化, 但总体上仍高于原有聚类算法的聚类精度, 进而验证了该算法的合理性和有效性.

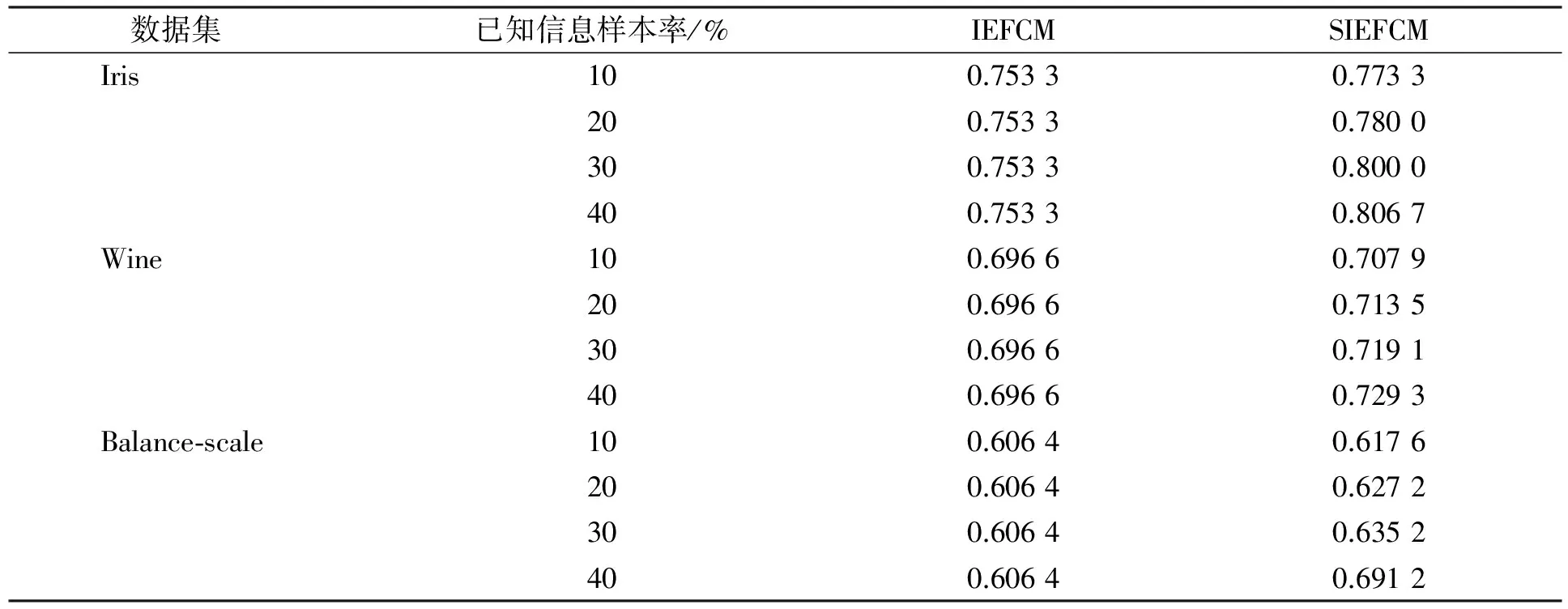
表2 实验结果RI的比较Table 2 Comparison of experimental results (RI value)

综上所述, 本文提出了一种新的基于信息熵的模糊C-均值半监督聚类算法, 在聚类过程中利用已知样本信息减少了信息的浪费, 同时考虑了类内紧度信息和类间分散度信息, 有效改善了基于信息熵无监督FCM聚类方法的盲目性.将本文方法在UCI数据集上进行仿真实验, 实验结果表明, 本文所提出的新算法总体上优于基于信息熵无监督FCM聚类算法的性能.

[1]Watts D J, Strogatz S H.Collective Dynamic of “Small-World” Networks [J].Nature, 1998, 393: 440-442.

[2]邢婷, 邢志国, 王凤领.基于信息熵的FCM聚类算法 [J].计算机工程与设计, 2010, 31(23)： 5092-5096.(XING Ting, XING Zhiguo, WANG Fengling.FCM Clustering Algorithm Based on Information Entropy [J].Computer Engineering and Design, 2010, 31(23)： 5092-5096.)

[3]李春芳, 庞雅静, 钱丽璞, 等.半监督FCM聚类算法目标函数研究 [J].计算机工程与应用, 2009, 45(14)： 128-132.(LI Chunfang, PANG Yajing, QIAN Lipu, et al.Objective Function of Semi-supervised FCM Clustering Algorithm [J].Computer Engineering and Applications, 2009, 45(14)： 128-132.)

[4]Amini M, Gallinari P.Semi-supervised Learning with Explicit Misclassification Modeling [C]//Proceedings of the 18th International Joint Conference on Artificial Intelligence.San Francisco: Morgan Kaufmann, 2003: 555-560.

[5]Bouchachia A, Pedrycz W.Enhancement of Fuzzy Clustering by Mechanisms of Partial Supervision [J].Fuzzy Sets and Systems, 2006, 157(13): 1759-1773.

[6]姚紫阳． 半监督中心最大化模糊C-均值算法 [J].计算机工程与应用, 2012, 48(33)： 188-193． (YAO Ziyang.Semi-supervised FuzzyC-Means Algorithm with Maximum Center Distance [J].Computer Engineering and Applications, 2012, 48(33)： 188-193.)

[7]CHEN Musong, WANG Shinnwen.Fuzzy Clustering Analysis for Optimizing Fuzzy Membership Function [J].Fuzzy Sets and Systems, 1999, 103(2): 239-254.

[8]唐亮, 黄培之, 谢维信.顾及数据空间分布特性的模糊C-均值聚类算法研究 [J].武汉大学学报: 信息科学版, 2003, 28(4): 476-479.(TANG Liang, HUANG Peizhi, XIE Weixin.A New Method of FCM Considering the Distribution of Spatial Data [J].Geomatic and Information Science of Wuhan University, 2003, 28(4): 476-479.)

[9]Bezdek J C, Hathaway R J, Sabin M J, et al.Convergence Theory for FuzzyC-Means: Connterexamples and Repairs [J].IEEE System, Man, and Cybernetics, 1987, 17(5): 873-877.

ImprovedFuzzyC-MeansClusteringAlgorithm

GUO Xinchen1, FAN Xiuling1, XI Xiantian1, HAN Xiao2
(1.CollegeofScience,NortheastDianliUniversity,Jilin132012,JilinProvince,China;
2.EditorialDepartmentofJournalofJilinUniversity,Changchun130012,China)

A new fuzzyC-means clustering algorithm was proposed by the introduction of functions of separation between clusters into FCM clustering algorithm and with the nature of semi-supervised learning considered.The model of semi-supervised FCM clustering algorithm with the information entropy as constraints was established and the solution to the model was derived.The simulation experiments were performed on UCI data sets to verify the effectiveness of the proposed algorithm.The experimental results show that this modified algorithm gets the better validity and performance.

semi-supervised clustering; fuzzyC-means algorithm (FCM); information entropy

2014-01-10.

郭新辰(1971—), 男, 汉族, 博士, 教授, 从事数据挖掘和机器学习的研究, E-mail: neduer@163.com.通信作者: 韩 啸(1981—), 男, 汉族, 博士研究生, 编辑, 从事数据挖掘和网络协同等的研究, E-mail: hanxiao@jlu.edu.cn.

国家自然科学基金(批准号: 11226263; 11201057; 61202261)和吉林省自然科学基金(批准号: 201215165).

TP181

A

1671-5489(2014)06-1293-04

10.13413/j.cnki.jdxblxb.2014.06.35

韩 啸)