零售业市场中具有学习效应的投资模型分析

王 国 栋

(重庆水利电力职业技术学院 基础部，重庆 402160)

通常完全理性博弈是基于两个假设：1)每个零售商在决策时，都具有完备的信息；2)每个零售商都是基于完全理性进行决策的.在现实中零售商之间的博弈是不断进行的，不可能立即达到Nash均衡状态，同时每个零售商掌握的信息都是不充分的，而且零售商决策都是由人做出的，而人由于感知认识能力和语言上的限制，所做出的决策也不可能是完全理性的，只能是有限理性[1-4].H.N.Agiza[5-7]等研究了非线性[8]成本函数下的有限理性多寡头博弈模型，并分析了模型的动力学特征.Tomasz Dubiel-Teleszynski[9]研究了规模不经济情况下的双寡头竞争.Z.Sheng[10]等研究了自适应调整参数以及一类产出模型的控制.虽然很多学者对具有有限理性博弈模型的分析较多，但是几乎所有的研究都认为投资者理性水平是一贯不变的，即投资者的理性水平并不会随着市场竞争过程的持续而动态变化，表现为投资者固守原来的投资策略，对于在市场竞争过程中获得新的信息没有吸收与利用，对自己的投资策略不能实现改进与优化，而有效应对市场的变化，吸收与利用已经了解到的信息等学习行为在现实中是客观存在的，特别是投资者为了生存、竞争与发展的需要，都存在刻意的积极的学习行为.因此考虑到学习效应的客观存在，随着市场竞争过程的发展，投资者所拥有的信息量也在不断增加，从而使得投资者的理性水平在市场竞争的动态过程中不断提升，这有助于投资者改进和优化原来的投资模式，实施更优的投资策略，以获取更大的市场竞争优势，实现利益最大化.目前研究投资者理性水平动态演化的文献尚不多，文献[11]从企业信息量和信息处理能力两个方面研究了企业理性水平随时间延续而不断提升的动态特征，但文章只是从概念与机理等方面开展了定性的研究；胡荣[12，13]在学习效应、有限理性与动态古诺竞争复杂性中研究了具有学习效应与自适应调整的动态模型的特点，并对模型的稳定性进行了研究，但文中逆需求函数与成本函数均为线性函数，此处就是在文献[12]的基础上将具有学习效应的有限理性古诺模型引入零售业市场，并考虑到市场的复杂性，成本函数为非线性更符合现实.

此处主要研究以下几个方面的内容，首先将具有学习效应与自适应调整的古诺模型引入零售业市场，考虑到市场的复杂性，假设成本函数为非线性，利用非线性理论对模型的稳定点进行了分析，最后对各参数的变化对系统稳定性的影响做了初步的探讨.

1 模型的建立

假设零售业市场由两个区域市场组成，分别记零售商A与零售商B销售同质产品，每个投资方的战略空间是选择投资的商品量，利润是支付，在t时期市场的总供应量为Q(t)=q1(t)+q2(t)，市场的逆需求函数为p=p(Q)=a-bQ，零售商的成本函数为C(q)=c+dq2，其中c表示零售商固定成本，d表示零售商的单位变动成本，其中a，b为正数，则第i家企业在第t期的税前利润模型为

(1)

第i家投资商在一个期间的边际利润为

(2)

由式(2)可以进一步求得零售商A在面对零售商B投资量决策的最优反应策略为(以下全文下标1表示零售商A，2表示零售商B)

(3)

式(3)表示零售商A具有完全理性时的最优反应决策，即零售商A掌握市场需求函数的完全信息，并了解竞争对手零售商B的投资量决策规律，能通过零售商B在t时期的投资量，准确预测到其在时期t+1的投资量，进一步做出自己t+1时期的最优反应决策.

由于现实中每个投资商并不具有完全的市场信息，也不可能完全预测未来的市场变化情况，因而他们的决策往往基于部分信息而做出，假设零售商A是基于上一期的边际利润做出有限理性调整，如果零售商A认为t期边际利润为正，则他将会在第t+1期增加投资量，反之如果边际利润为负，他就会减少投资量，于是可得到零售商A在第t+1期的投资模型为

(4)

其中α表示零售商A投资调整率.零售商B是采用学习效应的自适应调整机制，即零售商B具有学习效应，通过持续的市场竞争，零售商B的理性水平不断提高，投资模型为

(5)

其中θ2∈[0，1]，表示投资商B自适应调整参数，其中γ∈[0，1]表示学习效应指数，γ越小表示学习能力越强，特别地当γ=1时，表示投资商不具有学习效应.由式(4)(5)可以得到零售商A，B在t+1的投资模型为

(6)

2 模型的分析

显然E0，E1为有界均衡，E2为Nash均衡点.下面来研究这些均衡点的稳定性.首先求出式(6)的Jacobin矩阵，即

(7)

定理1 有界均衡E0，E1为不稳定均衡点.

证明在E0处的Jacobin矩阵为

可以求得J(E0)的两个特征值为λ1=1，λ2=θ2γ，因为|λ1|=1，|λ2|<1，所以E0为不稳定的鞍点.同理可以证明E1为不稳定的鞍点.E0对应的点为零售商A的投资量为零，此时零售商B占领市场，出现这种情况可能是由于零售商A的进货成本比较高，此时零售商A进一步提高企业对资源的吸附能力，而面对零售业市场的不成熟，会产生零售商对市场资源利用机会的不平等，也会导致零售商竞争力的下降，为了追求利润，另一家零售商必然会加入市场，从而开始了两家零售商的博弈.

定理2E2为Nash均衡稳定点.

证明在E2处的Jacobin矩阵为

(8)

它的特征方程为ρ(λ)=λ2-trJλ+detJ=0，其中trJ表示Jacobin矩阵的迹，detJ表示Jacobin矩阵的行列式.

(9)

(10)

(11)

说明矩阵J(E2)在Nash均衡点E2处有实特征值，如果J(E2)在均衡点E2的特征值都位于复平面的单位圆内，即|λi|<1，则Nash均衡点E2是局部稳定的，根据Jury条件，Nash均衡点E2是局部稳定的充要条件为1) 1-TrJ+DetJ>0;2) 1+TrJ+DetJ>0;3)|DetJ|<1.

对于条件1)是满足的，条件2)与条件3)决定了参数(α，θ2)平面上一个稳定区域，其边界曲线由直线α=0，θ2=0以及曲线

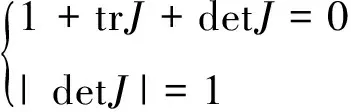
(12)

组成，E2在式(12)描述的区域内是稳定的结点，一旦α，θ2的取值超出这个区域，E2将变得不稳定.在式(12)的边界发生倍周期分叉失去稳定性. 值得注意的是双方是基于有限理性的，不可能立即达到Nash均衡状态，而需要双方的反复博弈，最终才能趋于平衡，一旦有一方，或者双方的投资调整率过快，或者学习效应极强，超过(α，θ2)的范围，都会导致系统的不稳定.

3 数值模拟分析

为了更好地了解动力系统(6)的动态行为，及更清晰地描绘投资者具有学习效应对系统动态行为的影响，取参数对系统(6)进行模拟分析，取参数a=15，b=1，c1=c2=0，d1=2，d2=2.2，θ2=0.1，初始值为q1(0)=1，q2(0)=2.

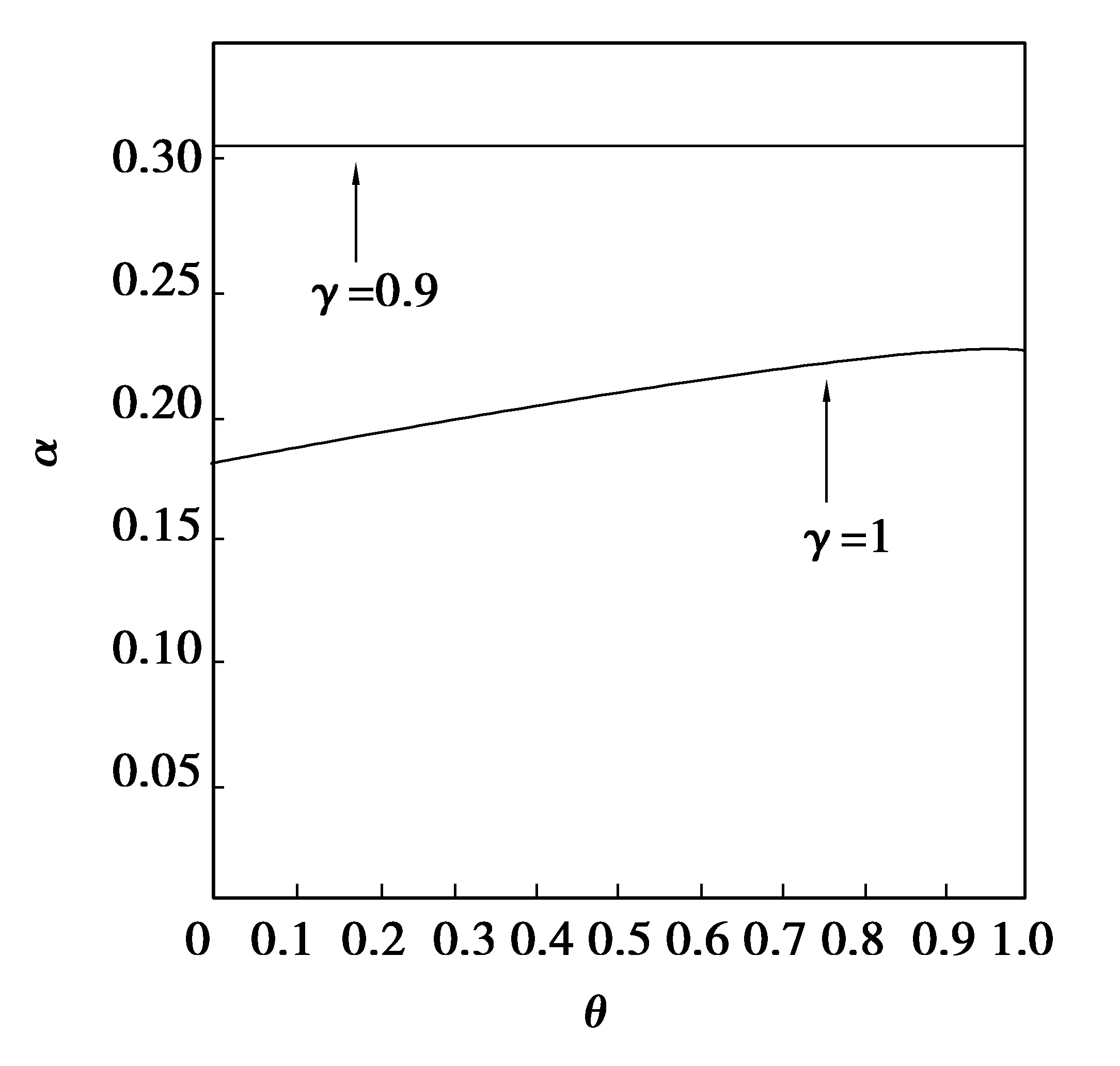
图1 系统(6)Nash均衡点的稳定区域

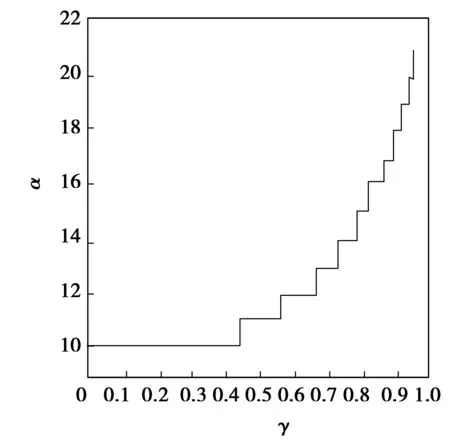
图2 学习效应对竞争到达均衡点的时间影响

图1表示零售商B学习效应指数为γ=1，γ=0.9时，Nash均衡点E2的稳定区域，从图上可以看出，具有学习效应的系统稳定区域明显要比没有学习效应的稳定区域要大，表明了学习效应的增强能有效增大系统Nash均衡点的稳定区域.当取参数α=0.15，其他参数不变的情况下，得到图2，表明了当系统(6)处于均衡状态时，学习效应对竞争到达均衡的时间的影响.从图2可以看出随着学习效应指数γ的减小，即学习效应的增强，到达均衡的时间不断缩短，特别是γ取值较大时，γ对均衡时间的影响更加明显.这说明学习效应的增强有利于加快系统到达均衡的速度，缩短系统到达均衡的时间.

4 小 结

为了模拟零售业市场中投资者不同的博弈行为，将具有学习效应的有限理性古诺模型引入零售业市场，考虑到零售业市场的复杂性，建立了一个非线性成本函数下的投资模型，利用非线性理论对模型的稳定点进行分析，得出了具有学习效应的系统稳定区域比没有学习效应的稳定区域要大，而且投资商随着学习能力的提高，双方达到均衡的时间会缩短.此处只是对具有学习效应投资模型进行了简单的分析，而且由于计算的复杂性，没有分析非线性成本函数下，参数对整个系统的影响，在以后将重点研究这部分的内容.

参考文献：

[1] AGIZA H N，HEGAZI A S，ELADDANY A A. Complex Dynamics and Synchronization of a Duopoly Game with Bounded Rationality[J]. Mathematics and Computer in Simulation，2002，58：133-146

[2] AGIZA H N，HEGAZI A S，ELAAD A A. The Dynamicsof Bowley’s Model with Bounded Rationality[J]. Chaos，Solitons and Fractals，2001(12)：1705-1717

[3] BISCHI G I，NAIMZADA A. Global Analysis of a Dynamic Duopoly Game with Bounded Rationality[A]. Dynamics Games and Application[C].Birkhouser，1999(5)：473-489

[4] 姚洪兴，徐峰.双寡头有限理性广告竞争博弈模型的复杂性分析[J]. 系统工程理论与实践，2005(12)：22-28

[5] AGIZA H N，ELASDANY A A. Nonlinear Dynamicsni the Cournot Duopoly Game with Heterogeneous Players[J]. Physica A，2003(320)：512-524

[6] AGIZA H N，HEGAZI A S，ELASADANY A A. Complex Dynamics and Syncheonization of a Duopoly Game with Bounded Rationality[J].Math Comput Simul，2002，58：133-146

[7] AGIZA H N，ELSADANY A A.Analysis of Nonlinear Triopoly Game with Heterogeneous Players[J].Computers and Mathematics with Applications，2009，57：488-499

[8] 刘锐，李树生. 无界域上二阶非线性脉冲边值问题解的存在性[J]. 重庆工商大学学报：自然科学版，2011，28(5)：441-443

[9] TOMASZ D T. Nonlinear Dynamics in a Heterogeneous Duopoly Game with Adjusting Players and Diseconomies of Scale [J]. Commun Nonlinear Sci numer Simulat，2011(16)：296-308

[10] SHENG Z，HUANG T，DU J，et al.Study on Self-adaptive Proportional Control Method for a Class of Outpul Models[J]. Discrete Contin Dynsyst Ser B，2009(11)：459-477

[11] 吴义爽.序贯理性与合约的渐进完备性：一个探索性研究[J].理论探索，2009，149(4)：163-167

[12] 胡荣. 学习效应，有限理性与动态古诺竞争复杂性[J].复杂系统与复杂性科学，2011(12)：44-50

[13] 胡荣.具有学习能力的有限理性双寡头竞争分析与混沌控制[J].控制与决策，2011，26(1)：133-136