基于中国股票市场的长记忆模型应用研究
2014-08-08秦玮
秦 玮
(重庆大学 数学与统计学院,重庆 401331)
在以往的金融时间序列研究中,一般都假设资产收益率为正态分布,而越来越多的研究结果表明,实际的股票收益率具有尖峰厚尾现象以及非对称性,正态分布并不能很好地刻画收益率的特征,因此许多学者选用偏t分布或其他分布代替正态分布,得到较好的拟合效果.Barndorff-Nielsen[1]在给沙丘运动建模时引入广义双曲线分布,并于1995年成功应用到金融领域中.Eberlein和Keller率先将双曲线分布用于金融领域研究,Barndorff-Nielsen研究了广义双曲线分布的另一子分布正态逆高斯分布.事实上,偏t分布是广义双曲线分布的极限分布,Prause,Barndorff-Nielsen,Shepard,Demarta和Mcneil等都对其做了深入研究[2].
自Hurst发现水文时间序列具有长记忆性以来,大量研究表明,金融资产收益率也呈现长记忆特征.收益率序列的绝对值或它的幂自相关衰减得十分缓慢,相距较远的时间间隔仍然具有显著的自相关性,表现为历史事件会长期影响未来.股票收益率长记忆性的存在意味着以此为理论假设基础的现代资本市场理论包括马柯维茨的资产组合理论、资本资产定价模型、套利定价理论和Black-Scholes期权定价模型在内的许多模型,都将面临严重的质疑和挑战.
Andersen,Bollerslev,Diebold&Ebens研究发现,用ARMA模型难以准确刻画序列的长记忆性,提出用自回归分整移动平均(ARFIMA)模型,它能较好地对序列的长记忆性进行刻画.ARFIMA(p,d,q)允许对序列进行分数d阶差分,综合考虑长记忆和短记忆过程,可用p+q个参数来描述短记忆过程,用参数d描述长记忆过程,比单纯地使用ARMA模型强.
将广义双曲线分布族与ARFIMA模型相结合,并在不同分布下对比ARFIMA模型的参数估计效果,还从时间和事件的角度分析了时间的划分对长记忆效应的影响.
1 广义双曲线分布简介
1.1 广义逆高斯分布
服从广义逆高斯(GIG)分布的混合随机变量与正态均值-方差变量相结合的变量服从广义双曲线(GH)分布.
定义1 如果一维非负的混合随机变量W服从GIG分布,Z~Nk(0,Ik),且W与Z独立.令
(1)
其中,位置参数μ∈Rd,漂移参数γ∈Rd,结构矩阵∑=AA′对称、正定,A∈Rd×k,则X服从广义双曲线(GH)分布.
对于不同的GIG分布将产生不同的GH分布.
由式(1)知,当混合变量W的方差存在时,则X的均值、协方差公式为
E(X)=μ+E(W)γ,COV(X)=E(W)∑+var(W)γγ′
(2)
一维的GIG分布的概率密度函数[2]为
(3)
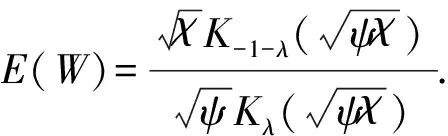
1.2 广义双曲线分布密度
根据式(1),由广义逆高斯(GIG)分布W~GIG(λ,χ,ψ)和Z~Nk(0,Ik),可推导出X的密度函数为
(4)
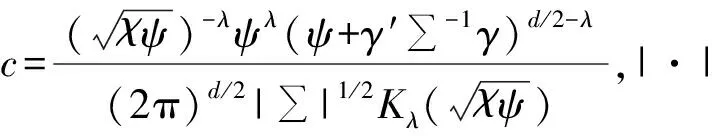
当混合函数W具有有限方差时,GH分布的均值和协方差为
1.3 一类特殊情形的广义双曲线分布
GH分布含有参数λ,χ,ψ,μ,∑,γ,当它们取特殊值时,会得到不同形式的广义双曲线密度.常用于金融数据分析的分布有如下几种.
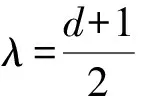
2) 正态逆高斯分布.当λ=-0.5时,GIG分布为逆高斯分布,对应的GH分布是正态逆高斯(NIG)分布,其概率密度函数可表示为
(5)
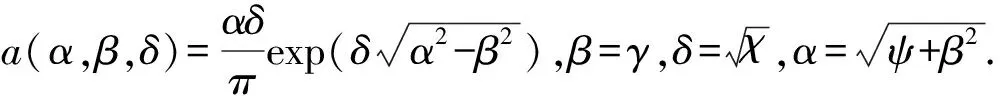
3) 偏t分布.当λ<0,ψ=0时,GIG转换为逆伽玛分布,逆伽玛分布IG(α,β)概率密度函数为
(6)
伽玛分布与逆伽玛分布之间具有如下关系:
如果X~Gamma(α,β),则X-1~IG(α,1/β).
当λ<0,ψ=0时,GIG随机变量X1~IG(-λ,χ/2).如果令λ=-v/2,χ=v,则逆伽玛分布对应的GH分布是偏t分布,v代表自由度.偏t分布的概率密度函数为
(7)
当γ=0时,偏t分布为对称t分布.服从偏t分布的随机变量X的均值和协方差为
(8)
1.4 广义误差分布
均值为0,方差为1的广义误差分布(GED)概率密度函数为
(9)
λ≡[2-2/vΓ(1/v)Γ(3/v)]0.5
(10)
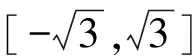
2 金融时间序列的长记忆性
2.1 时间序列的长记忆性定义
定义2 假设时间序列{xt}具有自相关函数ρτ,其中τ为滞后阶数.如果ρτ满足条件
(11)
则称{xt}为长记忆时间序列(Mcleaod和Hipel[3]).
定义3 如果平稳时间序列{xt}的自相关函数ρτ依负幂指数率(双曲率)τ-λ随滞后阶数τ的增大而缓慢下降,即
ρτ~Cτ2d-1,τ→∞
(12)
其中C表示常数,~表示收敛速度相同,d表示记忆性且2d-1=-λ,则称{xt}为长记忆时间序列(Brockwell[4]).
2.2 时间序列长记忆性的检验

(13)
其中,R(n)表示极差,即
(14)
S(n)表示标准差,即
(15)
可以证明
(16)
其中C为常数,H为Hurst指数.由式(16)可得H的近似估计值为
(17)
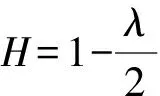
2.3 分整自回归移动平均(ARFIMA)模型
ARFIMA模型由Granger和Joyeux(1980)[5]提出,是基于分数差分噪声(FDN)模型与自回归移动平均(ARMA)模型相结合的产物.设{yt},t=1,2,…,T为可观测样本序列,则ARFIMA(p,d,q)模型表述如下
φ(L)(1-L)d(yt-μ)=θ(L)εt
(18)
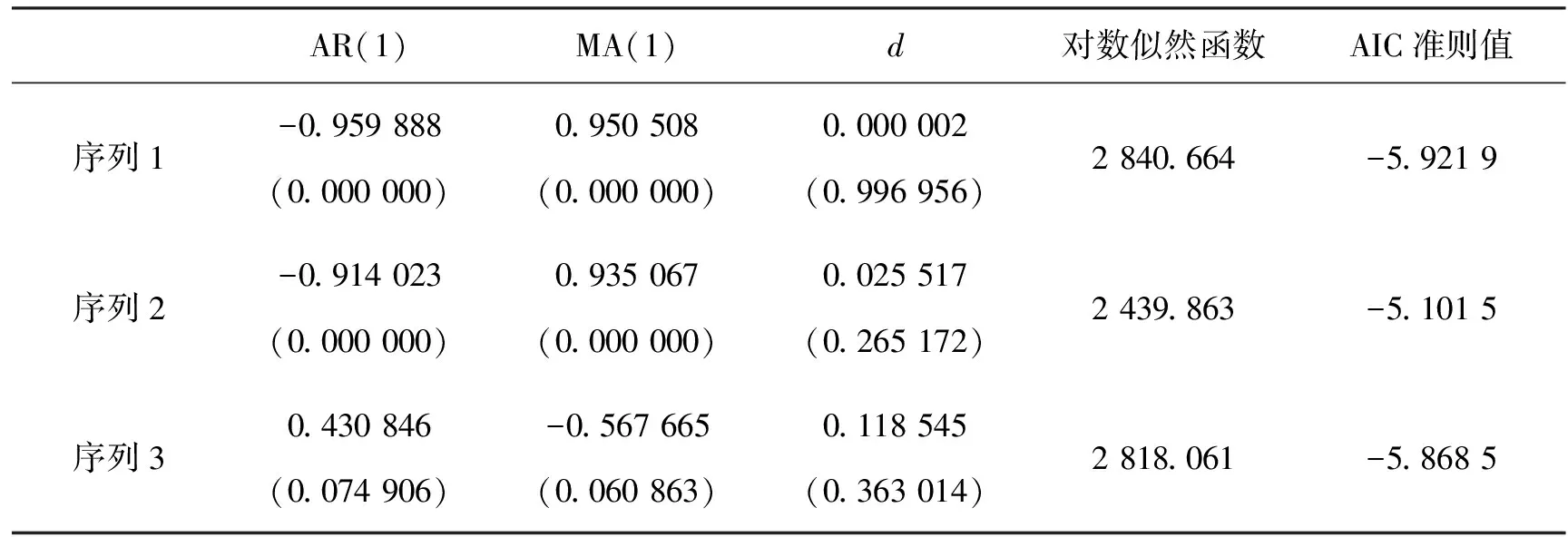
其中,{εt}是白噪声序列,L是滞后算子,滞后多项式算子φ(L)=1-φ1L-…-φpLp和θ(L)=1-θ1L-…-θqLq的特征根都在单位圆外,且|d|<0.5时,yt平稳且可逆;0 图2 收益率时间序列 由沪市和深市过去的指数波动分析可知,两者具有较大的相关性.沪市开市早、市值高,具有对外部冲击反应较敏感的特征,对深市具有一定的“溢出效应”,同时,上证指数与其他股票均具有极高的相关性和代表性.因此,此处选择上证指数作为研究样本.另外,在我国股票上市初期,进入流动的股票数量少,同时证券市场交易制度与监管制度也不完善,股票质量不高,股市呈现一定的大幅波动的现象,而在1997年后则呈现出平稳状态.此处选取1998年1月5日到2013年4月15日上证指数日收盘价格指数(数据源自华西证券http://www.hx168.com.cn/hxzq/index.jsp),样本总量为3 694个.将股票日收益率定义为yt=100*(lnpt-lnpt-1).收盘价时间序列如图1,收益率时间序列如图2. 首先对上证指数收益率序列进行描述统计和正态性W检验(表1),认为样本不是来自正态分布的总体.收益率的密度估计曲线和正态分布密度曲线的对比图也可以看出样本不服从正态分布(图3). 表1 数据描述统计和正态性W检验 根据AIC信息准则,均选用ARFIMA(1,d,1)模型.表2为各分布下ARFIMA(1,d,1)模型的估计结果.可以看出,正态分布下的模型估计效果不如其他模型,其长记忆性也并不显著.其他6种分布下的模型估计出的参数相差不大,象征长记忆性的d值均在0.23左右,属于0至0.5的区间内,p值也在99%的置信水平下显著,表明收益率序列具有长记忆性.通过各种分布的对比,显示出有偏分布下的模型估计效果都比对称分布下的模型估计效果要好,说明收益率序列的确具有尖峰厚尾性和非对称的效应. 表2 收益率序列在7种分布下ARFIMA(1,d,1)模型的估计结果 注:括号里的值为参数估计的p-value值. 图3 收益率的密度估计曲线与正态分布密度曲线 金融市场价格之所以波动,是因为它是市场各方面相互博弈的结果,因此事件尤其是重大事件必然会对金融市场产生深远影响.因此此处从时间和事件两个角度进行对比研究. 自2001年2月19日证监会作出对国内投资者开放B股市场以及同年6月12日国务院发布《减持国有股筹集社会保障金管理暂行办法》后,沪深股市一直低迷不振,进入熊市[7],2005年6月6日,上证指数跌破1 000点大关,随后股市开始单边上涨,进入牛市,2007年10月16日,上证指数达到开市以来最高点6 124点.而后,受到金融风暴等因素的影响,自2008年暴跌后,股市又呈现颓靡的熊市.因此将上证指数数据划分为3个序列,序列1的时间跨度为2001年6月13日至2005年6月5日,共957个数据;序列2的时间跨度为2005年6月6日至2009年5月5日,共954个数据;第3个序列的时间跨度从2009年5月6日至2013年4月15日,共958个数据.选用的模型为在偏学生t分布下的ARFIMA(1,d,1)模型,结果见表3. 表3 3个序列在偏学生t分布下的ARFIMA(1,d,1)模型的估计结果 注:括号里的值为参数估计的p-value值. 虽然表3中结果没有表2数据的结果理想,长记忆性没有那么显著,但依然表明不同时间划分下不同时间段的长记忆效应不同.序列1的d值几乎为0,有理由相信这一时间段没有长记忆性.序列2的d值也很小,仅为0.025 517,说明序列2的长记忆性也不明显.相对来说,序列3的长记忆性比序列1和2的长记忆性稍稍显著一些,但也不如上一组数据,即1998年1月5日到2013年4月15日这一时间段的收益率序列的长记忆性明显. 采用上证指数作为样本建立了广义双曲线分布簇下的ARFIMA模型,实证分析结果表明上证指数收益率序列具有尖峰厚尾性和非对称效应的长记忆特征.针对不同分布的计算结果比较,表明有偏分布更适合用来拟合上证指数收益率.由于事件的发生对上证指数有一定的影响,因此,时间段的选取是一个重要的因素,不同时间段的收益率序列的长记忆效应是不同的.另外,将划分前后不同时间跨度的时间序列相比较,可以发现时间跨度短的时间序列的长记忆性不如时间跨度长的时间序列显著,但也并不能说明时间越长,长记忆效应越显著. 参考文献: [1] BARNDORFF-NIELSEN O. Exponentially Decreasing Distributions for the Logarithm of Particle Size[J]. Proceeding of Royal Society ofLondon,Series A,1977(353):401-419 [2] 张建龙,林清泉. GH分布族下资产收益率分布拟合优度比较——基于中国证券指数高频数据的实证研究[J]. 数学的实践与认识,2010(11):26-33 [3] MCLEOD A L,HIPEL K W. Preservation of The Rescaled Adjusted Range,1:A Reassessment of the Hurst Phenomenon[J]. Water Resources Research,1978(14):491-508 [4] BROCKWELL P J,DAVIS R A.Time Series:Theory and Methods[M]. Spinger-Verlag,1991 [5] GRANGER C W J,JOYEUX R. An Introduction to Long Memory Time Series Models and Fractional Differencing[J]. Journal of Time Series Analysis,1980(1):44-67 [6] 曹广喜. 我国股市收益的双长记忆性检验——基于VaR估计的ARFIMA-HYGARCH-skt模型[J]. 数理统计与管理,2009(1):167-174 [7] 石纪信,方兆本. 牛熊市视角下我国股市波动率的长记忆性研究[J]. 中国科学技术大学学报,2012(3):179-184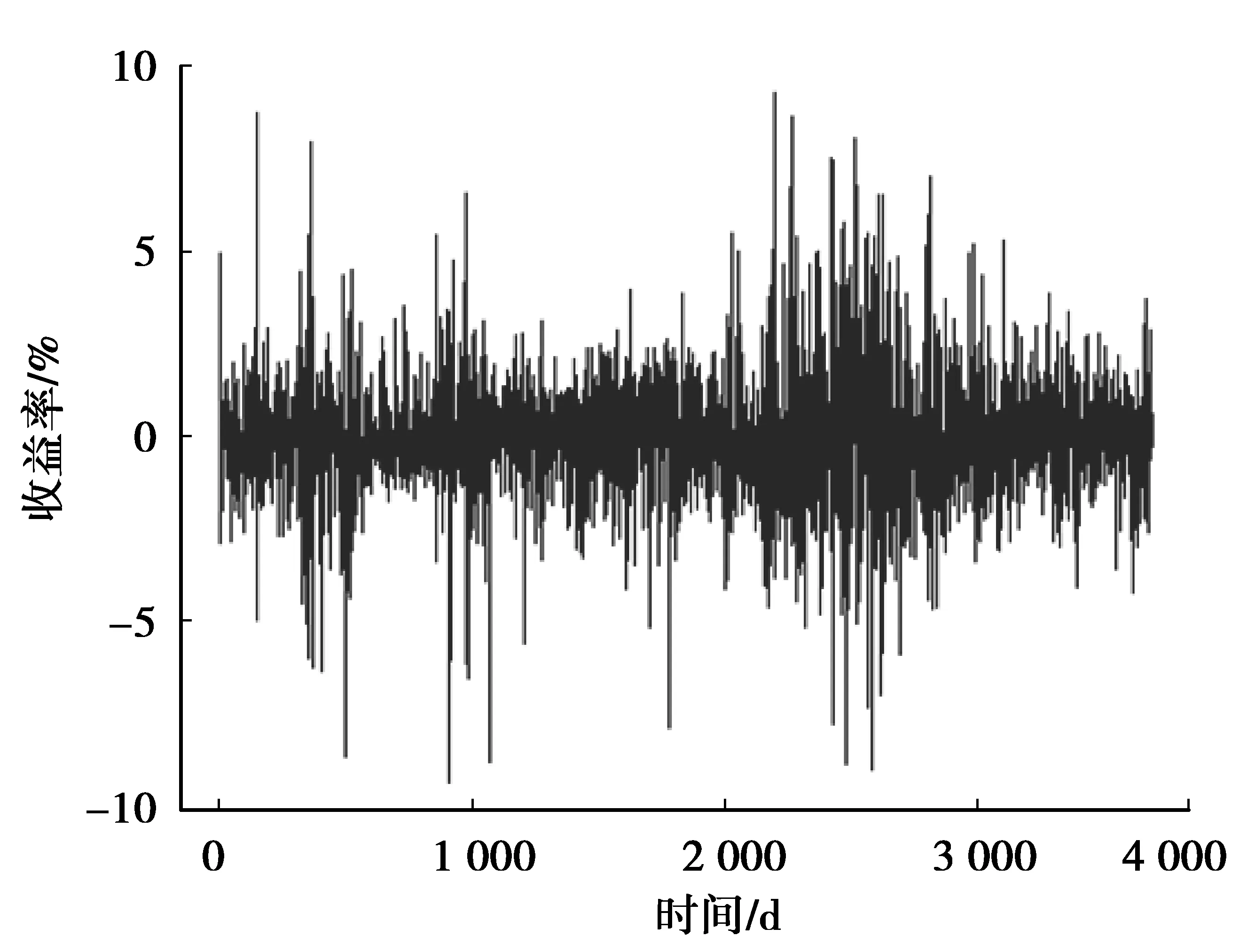
3 实证分析
3.1 样本数据的选取
3.2 样本数据描述统计

3.3 长记忆性检验及结果分析


3.4 时间和事件对长记忆检验的影响
4 结 论
