风险投资最优组合*

张 浩， 侯为波

(淮北师范大学 数学科学学院，安徽 淮北 235000)

0 引 言[1]

在现实的投资问题中，有涉及多种资产的风险投资组合.随着数学和金融学的不断发展，投资者已经不满足于单纯盈亏的定性分析，而是希望对风险与收益做出综合的分析，找出一种收益最大，风险最小的最优投资组合.例如，投资市场上有m种投资方式It以供投资者选择，某投资者有金额为P的资金来进行一段时期的投资.分析人员评估了这m种资产，估算得出要想购买It的风险损失率为Bt，平均收益率为At.因为投资越分散，其总风险就越小，投资人可以确定，当用这些资金来购买若干的资产时，总风险可以被投资方式It中最大的风险所代替.购买It要交交易费，并且若It≤Ut(Ut为定值)，交易费按购买金额计算.还有假定银行利率为A0(A0=0.04)，并且银行利率既无风险又无交易费.假定m=4时的相关数据如表1，求在该数据下的最优风险投资组合.

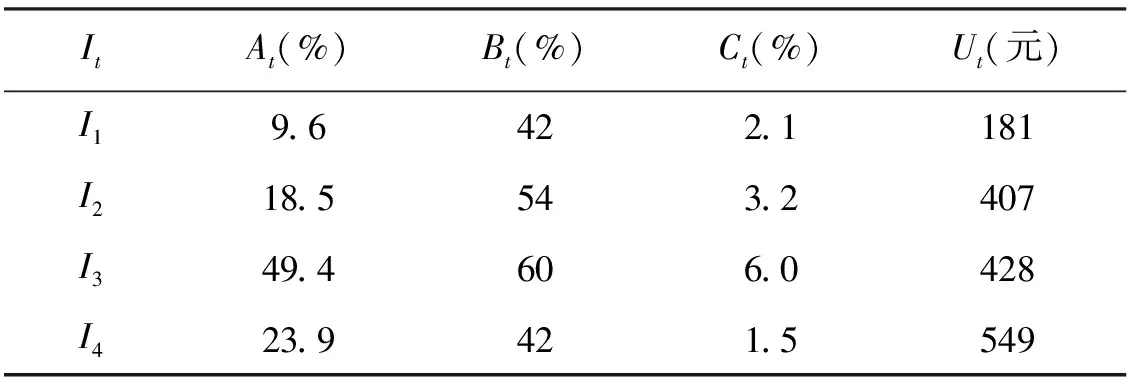
表1 m=4时最优风险投资组合

1 分析问题

由于不确定的资产预期收益性，使得投资具有风险性，投资者都希望投资的总风险最小而总收益却最大，所以投资者往往采取投资组合的方法来使风险分散化.在风险损失最小情况下，得到最大的预期收益的投资组合，就是最优的风险投资组合.

此处在讨论风险与收益的基础上，给出相关数据，通过分析、计算，找出最优的风险投资组合.其中最优是指：1) 在收益一定的情况下风险最小；2) 在风险一定的情况下收益最大.每个投资者的投资心态和环境不同，只能根据大部分的投资情况找到一个大多数投资者都能接受的风险范围内所得到的收益最大的投资方案.

2 建立最优风险投资组合模型

每种投资所需的交易费为Ct，根据交易费的计算规则得出

(1)

如果不投资It，则Kt=0，可得出Ct=0，即若不投资It就不必支付交易费；若投资It，则投资金额P×Kt与交易额支付定值Ut做比较，取两者之中大的与该投资的交易费率相乘，即为该投资所要支付的交易费.

(2)

最后对投资的总风险与净收益做出个双规划模型

(3)

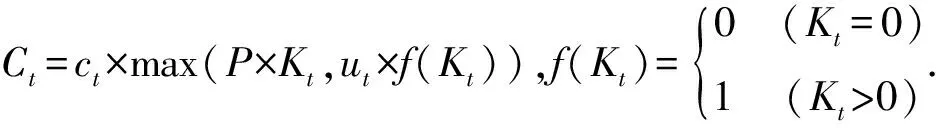
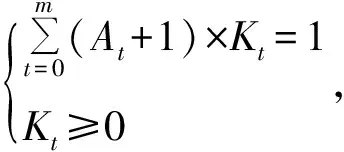
(4)

在式(4)中，第1个目标函数是求最大值的，而第2个目标函数是非线性的，这就使得求解很麻烦.要想办法把非线性问题转化为线性问题，把求最大值转化为求最小值，于是就得到了模型(5)

(5)

3 模型求解

模型(5)是有约束条件的双目标线性规划求最优解的问题，用偏好系数加权法，将模型中的两个目标加权重合得到一个单目标线性规划[3].设s和1-s分别表示为投资者对总风险和净收益的权重.于是原模型就变为单目标线性规划问题

(6)

其中权重数s与1-s分别表示投资者对总风险大小和净收益大小的重视程度，s的取值范围为[0，1]，s的取值越大，说明投资者对总风险重视程度越大.当1-s=1，s=0，说明投资者只关心净收益而忽略总风险，这是种投机心理；当1-s=0，s=1，说明投资者只关心风险程度而不关心净收益，该投资者非常的稳重.

假设当s=0.5时，解得结果为

x=[0.126 9，0.502 4，0.227 9，0.142 8]

4 小 结

由于投资者的投资心态与投资环境不同，所以模型对两种决策因素采取了偏好系数加权的方法.这里的最优方案是在某一个特定的偏好系数下收益期望值较高而风险较小的投资方案.实际上，在求解过程中，不同的偏好系数所得到的最优方案也是不一样的.

参考文献：

[1] 安实，王健，赵泽斌.风险投资理论与方法[M].北京：科学出版社，2006

[2] 张春宁，蔡敬梅，张延锋.一种新的风险投资组合模型构建方法[J].统计研究，2003，20(11)：57-63

[3] 茆诗松.概率论与数理统计教程[M].北京：高等教育出版社，2004