交换环上的强w-投射模

周德川, 王芳贵

(四川师范大学数学与软件科学学院,四川成都610066)

本文提到的环都是有单位元的交换环.2012年,X.H.Fu等[1]引入了余纯投射模的概念.R-模M称为余纯投射模,是指对一切平坦模F,有熊涛等[2]借助余纯投射模来刻画CPH环的结构(每个余纯投射模的子模是余纯投射模),并讨论了CPH环与遗传环的关系.本文在此基础上定义了强w-投射模,是指对一切无挠w-模M,有,强w-投射模是介于投射模与余纯投射模之间的模,通过对强w-投射模的讨论,给出了遗传环和半单环的一个新的刻画,也给出了一个DW-环的同调刻画.

1 强w-投射模

设R是交换环,S是R的所有非零因子的乘法集,M是R-模.令

则T(M)是M的子模.当T(M)=M时,M称为挠模;当T(M)=0时,M称为无挠模.注意,T(M)总是挠模,M/T(M)总是无挠模.为了给出强w-投射模的定义,首先来看投射模的一个等价刻画.

命题1.1对环R,R-模P为投射模当且仅当对任意的无挠模A,都有

证明若对任意的无挠模A,都有=0,设0➝K➝F➝P➝0是正合列,其中F是自由模,K=ker(F➝P),由于F是无挠模,从而K是无挠模,由条件,故

是正合列,则正合列0➝K➝F➝P➝0分裂,即有F≅PK,故P为投射模.反之显然成立.

1997年,F.G.Wang等[3]引入了整环上的w-模的概念,2011年,H.Y.Yin等[4]把w-模的概念推广到一般交换环上.设J是R的有限生成理想.若自然同态R➝HomR(J,R)是同构,则J称为R的GV-理想.用GV(R)表示R的GV-理想的集合.对R-模M,定义

则GV-tor(M)是M的子模.当GV-tor(M)=M时,M称为GV-挠模;当GV-tor(M)=0时,M称为GV-无挠模.若M是GV-无挠模,且对所有J∈GV(R),,则M称为w-模.1997年,文献[5]还引入了w-投射模的概念.R-模M称为w-投射模,是指对任何无挠的w-模N,是GV-挠模.

定义1.2R-模P称为强w-投射模,是指对任何无挠w-模M,都有

例1.31)显然,投射模是强w-投射模;强w-投射模是w-投射模;

2)任何GV-挠模都是强w-投射模.特别地,若J是R的GV-理想,则R/J是强w-投射模;

3)强w-投射模未必是投射模.例如,设R是最大公因子整环,a1,a2∈R互素,则J=(a1,a2)是R的GV-理想,于是R/J是GV-挠模.从而有R/J是强w-投射模.由于R/J也是挠模,故R/J不是投射模.

命题1.4设0➝A➝B➝C➝0是正合列.若A、C是强w-投射模,则B是强w-投射模.

证明设M是任意的无挠w-模,则有正合列,由于A、C是强w-投射模,所以,由定义知B是强w-投射模.

命题1.5设{Pi}是一簇模,则是强w-投射模当且仅当每一Pi是强w-投射模.

证明设M是任意的无挠w-模,由自然同构即得证.

命题1.6若0➝M➝F➝P➝0是分裂的正合列,则M、P是强w-投射模是当且仅当F是强w-投射模.

命题1.7对环R,M是强w-投射模.

1)若P是投射模,则是强w-投射模;

2)若P是有限生成投射模,则HomR(P,M)是强w-投射模.

证明1)设X是任意的无挠w-模.若P是投射模,由文献[6]的定理4.5.9有

由于M是强w-投射模,所以

2)设X是任意的无挠w-模,若P是有限生成投射模,由文献[6]的定理4.5.11有

定理1.8对模M,以下各条等价:

1)P是强w-投射模;

2)设0➝A➝B➝P➝0是正合列,则对任意的无挠w-模M,有正合列

3)设A是B的子模,M是无挠w-模,若B/A≅P,则对任何同态f:A➝M可以扩张到B;

4)对任意正合列0➝M➝B➝P➝0是分裂的正合列,其中M是无挠w-模;

5)对正合列0➝A➝B➝C➝0,其中A是无挠w-模,有

6)对正合列0➝A➝E➝C➝0,其中A是无挠w-模,E是内射模,有

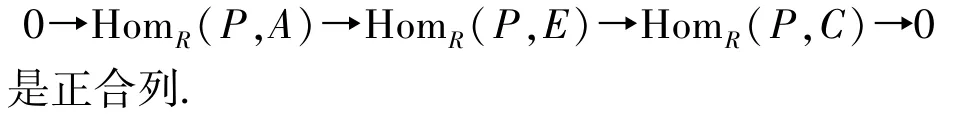
证明1)⇒2) 由已知可得到正合列

2)⇒3) 0➝A➝B➝B/A➝0是正合列,由于B/A≅P,则由2)有正合列

所以对任何同态f:A➝M可以扩张到B.

3)⇒4) 0➝M➝B➝P➝0是正合列,则有B/M≅P,所以对同态f:M➝M可以扩张到B➝M的同态.所以正合列0➝M➝B➝P➝0分裂.

4)⇒1) 由文献[7]的推论7.20即可得到.

1)⇒5) 由已知条件有正合列

5)⇒6) 平凡的.

6)⇒1) 设A是无挠的w-模.取正合列0➝A➝E➝C➝0,其中E是内射模,则有正合列

由假设知,故P是强w-投射模.

由文献[5]引理知f是同构的,所以有,则P是强w-投射模.

命题1.9P是强w-投射模,则P是投射模当且仅当pdRP≤1.

证明设0➝K➝F➝P➝0是正合列,其中F是自由模,由于pdRP≤1,于是K是投射模,从而是无挠w-模,由定理1.8知此正合列分裂,故P是投射模.反之显然成立.

推论1.10设R是环,若gl.dim(R)≤1,则强w-投射模是投射模.

引理1.11设0➝A➝B➝C➝0是正合列.如果A是挠模,B是强w-投射模,则C是强w-投射模.

证明设B是强w-投射模,M是无挠w-模,由定义由于A是挠模,M是无挠模,所以HomR(A,M)=0.由

是正合列知,所以C是强w-投射模.

命题1.12对环R,P是强w-投射模,则P/T(P)是强w-投射模.

证明0➝T(P)➝P➝P/T(P)➝0是正合列,其中T(P)是挠模,P是强w-投射模,由引理1.11知P/T(P)是强w-投射模.

推论1.13对环R,P是挠模且是强w-投射模,则P的任何商模都是强w-投射模.

引理1.14对模M,以下等价:

1)M是w-模;

2)对任何正合列0➝M➝F➝N➝0,只要F是w-模,则有N是GV-无挠模;

3)存在一个正合列0➝M➝F➝N➝0,其中F是w-模,N是GV-无挠模.

证明参见文献[4]的命题2.7.

定理1.15GV-无挠的强w-投射模是投射模.

证明设P是GV-无挠的强w-投射模.取正合列0➝M➝F➝P➝0,其中F是自由模.由引理1.14,M是无挠w-模,于是有由文献[7]的推论7.20,此正合列分裂,从而有P是投射模.

2 对半单环、DW-环和遗传环的新刻画

对半单环,有很多关于它的刻画,例如R是半单环当且仅当每个R-模是投射模;当且仅当R的每个理想是R的直和加项等.用强w-投射模,可以给半单环一个新的刻画.

定理2.1对环R,以下等价:

1)R是半单环;

2)每一R-模是强w-投射模;

3)每一GV-无挠R-模是强w-投射模.

证明1)⇒2)⇒3) 显然.

3)⇒1) 设A是R的理想,则A是GV-无挠模.由条件,A是强w-投射模.由定理1.15,A是投射模,从而是w-模.由引理1.14,R/A是GV-无挠模,由条件R/A是强w-投射模,仍用定理1.15有R/A是投射模,于是正合列0➝A➝R➝R/A➝0分裂,故A是R的直和加项,从而有R是半单环.

回顾环R称为DW-环是指环R的每个理想都是w-理想.R为DW-环当且仅当R的GV-理想仅有R自身;当且仅当每一R-模是w-模,DW-环的讨论可参见文献[8],对于整环,也可参见文献[9].可用强w-投射模给出DW-环的一个同调刻画.

命题2.2设R是交换环,则强w-投射模是投射模当且仅当R是DW-环.

证明设J∈GV(R),则R/J是GV-挠模,由例1.3知GV-挠模是强w-投射模,由条件知R/J是投射模,而投射模是GV-无挠模,所以R/J=0,即是J=R.所以R是DW-环.

反之,若R是DW-环,则任意R-模是w-模.由w-模是GV-无挠模及定理1.15知强w-投射模是投射模.

也可以用强w-投射模来刻画遗传环.

定理2.3对交换环R,以下等价:

1)R是遗传环;

2)强w-投射模的子模是强w-投射模;

3)投射模的子模是强w-投射模;

4)自由模的子模是强w-投射模;

5)每个无挠w-模的内射维数不超过1;

6)R的每个理想是强w-投射模.

证明1)⇒2)R是遗传环,则gl.dim(R)≤1,由推论1.10知强w-投射模是投射模,又由于R是遗传环,则投射模的子模是投射模,所以强w-投射模的子模是投射模,故是强w-投射模.

2)⇒1) 投射模是GV-无挠模,其子模也是GV-无挠模.又由于投射模是强w-投射模,由条件投射模的子模是强w-投射模,由定理1.15知GV-无挠强w-投射模是投射模,所以投射模的子模是投射模,故R是遗传环.

2)⇒3) 平凡的.

3)⇒4) 平凡的.

4)⇒2) 设0➝A➝B➝C➝0是正合列,其中B是强w-投射模.取自由模F与满同态h:F➝B,则α=gh也是满同态.令K=ker(α),则有如图1所示的正合列的交换图.

注意图1左边方图是推出图,从而有正合列0➝K➝FA➝B➝0,由假设,K是强w-投射模,由命题1.4知FA是强w-投射模,由命题1.5,A是强w-投射模,得证.

图1

1)⇒5) 设M是的无挠w-模,对任意模X,有正合列0➝A➝P➝X➝0,其中P是投射模,A=ker(P➝X),由于R是遗传环,所以A是投射模,有正合列

5)⇒3) 设P是任意的投射模,A是P的任意子模,有0➝A➝P➝X➝0是正合列,其中X≅P/A.对任何无挠w-模M,有正合列

4)⇒6) 显然.

6)⇒5) 设M是无挠w-模,I是R的任何理想,有0➝I➝R➝R/I➝0 是正合列,则

致谢四川师范大学研究生优秀论文培育基金(校研字20131434)对本文给予了资助,谨致谢意.

[1]Fu X H,Zhu H Y,Ding N Q.On copure projective modules and copure projective dimensions[J].Commun Algebra,2012,40(1):343-359.

[2]熊涛,王芳贵,胡葵.余纯投射模与CPH环[J].四川师范大学学报:自然科学版,2013,36(2):198-201.

[3]Wang F G,McCasland R L.Onw-modules over strong Mori domains[J].Commun Algebra,1997,25(4):1285-1306.

[4]Yin H Y,Wang F G,Zhu X S,et al.w-modules over commutative rings[J].J Korean Math Soc,2011,48(1):207-222.

[5]Wang F G.Onw-projective modules andw-flat modules[J].Algebra Colloquium,1997,4:111-120.

[6]王芳贵.交换环与星型算子理论[M].北京:科学出版社,2006.

[7]Rotman J J.An Introduction to Homological Algebra[M].New York:Academic Press,1979.

[8]王芳贵.有限表现型模与w-凝聚环[J].四川师范大学学报:自然科学版,2010,33(1):1-9.

[9]Mimouni A.Integral domains in which each ideal isw-ideal[J].Commun Algebra,2005,33:1345-1355.

[10]Kasch F.Modules and Rings[M].London:Academic Press,1982.

[11]赵松泉,王芳贵,陈翰林.交换环上的w-模是平坦模[J].四川师范大学学报:自然科学版,2010,35(3):364-366.

[12]Stenström B.Coherent rings and FP-injective modules[J].J London Math Soc,1970,2:323-329.

[13]Lucas T M.Strong Prüfer rings and the ring of finite fraction[J].Pure Appl Algebra,1993,84:59-71.

[14]Lucas T M.The integral closure ofR(X)andR〈X〉[J].Commun Algebra,1997,25:847-872.

[15]Lucas T M.Characterizing whenR[X]is integrally closed(II)[J].Pure Appl Algebra,1989,61:49-52.