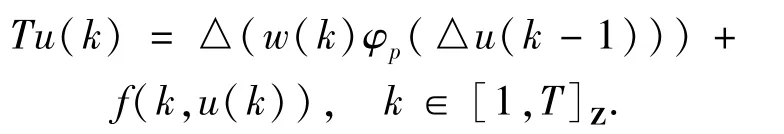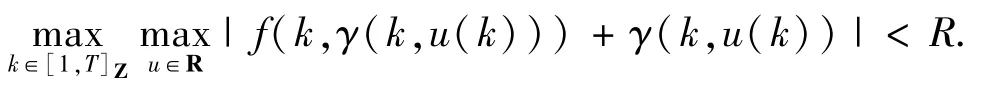一维离散p-Laplacian边值问题多个解的存在性
2014-08-07谢春杰
景 兰, 谢春杰
(1.兰州职业技术学院,甘肃兰州730070; 2.西北师范大学数学与统计学院,甘肃兰州730070)
1 引言及预备知识
非线性差分方程广泛应用于研究计算机科学、经济学、神经网络、生态学及控制论等学科中出现的离散模型.近年来,对于非线性差分边值问题已经有很多人研究过,见文献[1-12]及其参考文献.特别地,1997年,R.P.Agarwal等[1]运用上下解方法获得了二阶离散边值问题
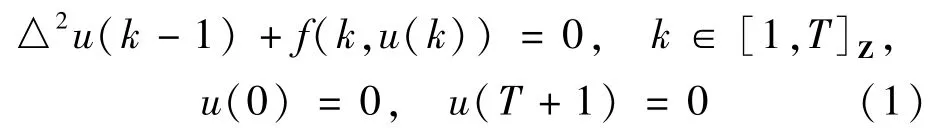
解的存在性.2005年,R.P.Agarwal等[7]运用变分法讨论了一维离散p-Laplacian边值问题
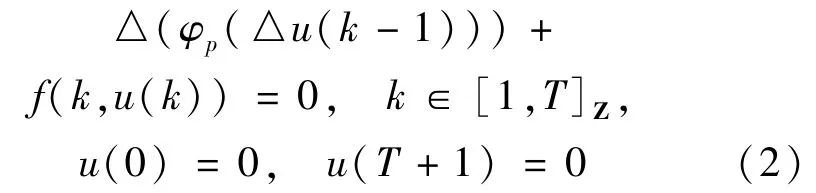
2个解的存在性.对于问题(2)解的存在性已经被许多人研究过,见文献[8-12]及其参考文献,但据我们所知,对于问题(2)多个解的存在性研究较少.受以上文献的启发,本文运用Brouwer度理论[13]发展一维离散p-Laplacian边值问题

的上下解方法,并讨论其多个解的存在性,其中,[1,T]Z:={1,2,…,T-1,T},φp(s)=|s|p-2s,p>1,f:[1,T]Z×R➝R连续,R=(-∞,+∞),w(k):[1,T+1]Z➝(0,+∞).
本文运用Brouwer度理论[13]发展了问题(3)的上下解方法,并获得了其多个解的存在性,见定理2.2,该结果是对文献[1]中定理3.1的推广,也是对问题(2)多个解存在性的发展.此外,相应的连续形式的一维p-Laplacian边值问题多个解的存在性结果,参见文献[14-16].
记E={u∈RT+2,u=(u(0),u(1),u(2),…,u(T),u(T+1))}.
定义1.1对∀u,v,w∈E有
1)若对∀k∈[0,T+1]Z,u(k)≤v(k),记u≤v;
2)若对∀k∈[1,T]Z,u(k) 3)若w≺u≺v,记u∈(w,v). 定义1.2对∀α,β∈E,称α是问题(3)的下解,如果 称β是问题(3)的上解,如果 当不等式(4)和(6)是严格不等式时,称α和β分别是问题(3)的严格下解和严格上解. 定义空间E0={u∈E,u(0)=u(T+1)=0},其基本元素记为(u(1),u(2),…,u(T)),与RT+2中元素(0,u(1),u(2),…,u(T),0)相对应,则方程(3)的差分算子在E0上有定义.定义范数,则空间E0按该范数‖·‖构成Banach空间. 定义连续算子T:E0➝RT为 定理2.1设α和β分别是问题(3)的下解和上解,且α≤β,则问题(3)至少存在一个解u满足α≤u≤β.当α和β分别是问题(3)的严格下解和上解时,则∃R>0,使得d(T,Ωαβ,0)=1,其中 证明定义函数γ(k,u(k)):[1,T]Z×R➝R如下 第1步证明若辅助问题(8)存在解 则α≤u≤β.下面证α≤u,u≤β同理可证. 反设∃i∈[0,T+1]Z,使得α(i)>u(i).因α(0)≤0,α(T+1)≤0,则∃m∈[1,T]Z有 从而结合φp为增函数可得 而由下解α的定义得 与(9)式矛盾.因此α≤u. 第2步用Brouwer度证明辅助问题(8)至少存在一个解. 定义连续算子:E0➝RT为 则显然辅助问题(8)的解是在E0中的零点.定义同伦 由f的连续性及γ的定义得,∃R>0使得 假设(λ,0,u(1),…,u(T),0)∈[0,1]×E0是Γ(λ,u)=0的一个可能的解,即u∈E0满足 由Brouwer度的同伦不变性得 因此d(,BR(0),0)=1,则辅助问题(8)至少存在一个解. 综上所述,若α和β分别是问题(3)的下解和上解,且α≤β,则问题(3)至少存在一个解u∈E0使得α≤u≤β,且∃R>0,有d(T,BR(0),0)=1. 第3步证明当α和β分别是问题(3)的严格下解和严格上解时,对第2步中定义的R>0,有d(T,Ωαβ,0)=1,其中 因α和β分别是问题(3)的严格下解和严格上解,则α和β也是问题(3)上解和下解.由第1步和第2步得α≤u≤β.下证α≺u≺β.先证α≺u成立.因为α(0)≤0,α(T+1)≤0,只需证明对∀k∈[1,T]Z,α(k) 结合严格下解α的定义得 与(13)式矛盾.因此α(k) 同理可证u≺β. 综上可得α≺u≺β,且由第2步知,‖u‖ 则辅助问题(8)至少存在一个解u,且u∈Ωαβ.在Ωαβ上T=,由 Brouwer度的切除性得 定理2.2假设问题(3)存在2个严格下解α1和α2以及2个严格上解β1和β2满足 且∃k∈[0,T+1]Z,有β1(k)<α2(k),则问题(3)至少存在3个解u1、u2和u3且满足 证明对于定理2.1中存在的R>0,定义开集Ωα1β2、Ωα1β1和Ωα2β2如下 运用定理2.1得 (14)~(16)式结合Brouwer度的切除性可得 由(15)~(17)式可得问题(3)至少存在3个解u1、u2和u3满足 [1]Agarwal R P,O’Regan D.Boundary value problems for discrete equations[J].Appl Math Lett,1997,10(4):83-89. [2]Hederson J,Thompson H B.Existence of multiple solutions for second-order discrete boundary value problems[J].Comput Math Appl,2002,43:1239-1248. [3]Rachrunkova I,Rachrunek L.Solvability of discrete dirichlet problem via lower and upper functions method[J].J Difference Equ Appl,2007,13(5):423-429. [4]Agarwal R P,O’Regan D.Difference equations in abstract spaces[J].J Austral Math Soc,1998,A64:277-284. [5]Bereanu C,Mawhin J,Neuve L.Exitence and Multiplicity results for nonlinear second order difference equations with Dirichlet value conditions[J].Math Bohemica,2006,2:145-160. [6]Wang D,Guan W.Three positive solutions of boundary value problems forp-Laplacian difference equations[J].Comput Math Appl,2008,55:1943-1949. [7]Agarwal R P,Perera K,O’Regan D.Multiple positive solutions of singular discretep-Laplacian problems via variational methods[J].Adv Diff Eqns,2005,2(2005):93-99. [8]Cabada A,Iannizzotto A,Tersianc S.Multiple solutions for discrete boundary value problems[J].J Math Anal Appl,2009,356:418-428. [9]Jiang D,Pang P Y H,Agrwal R P.Upper and lower solutions method and a superlinear singular discrete boundary value problem[J].Dynamic Systems and Applications,2007,16:743-754. [10]Jiang D,Zhang L,O’Regan D,et al.Existence theory for single and multiple solutions to singular positone discrete Dirichlet boundary value problems to the one-dimensionp-Laplacian[J].Archivum Mathematicum,2004,40:367-381. [11]Zhu B,Yu J.Multiple positive solutions for resonant difference equations[J].Math Comput Model,2009,49:1928-1936. [12]Rachrunkov’aI,Tisdellb C C.Existence of non-spurious solutions to discrete Dirichlet problems with lower and upper solutions[J].Nonlinear Anal,2007,67:1236-1245. [13]Sun J,Zhao Y.Existence of positive solution for second-order nonlinear discrete system with parameter[J].Math Comput Modelling,2005,41:493-499. [14]Zhou G.Existence of multiple positive solutions of discrete boundary value problem[J].Chin Quart J Math,2002,17(4):12. [15]Hu W,Jun W.A generalized upper and lower solution method for singular discrete boundary value problem[J].Chin Quart J Math,2007,22(2):212-219. [16]Cheung W,Ren J,Patricia J Y W,et al.Multiple positive solutions for discrete nonlocal boundary value roblems[J].J Math Anal Appl,2007,330:900-915. [17]Ma R Y,Lu Y Q,Chen T L.Existence of one-signed solutions of discrete second-order periodic boundary value problems[J/OL].Abstr Appl Anal,2012,2012,Article ID 437912.http://dx.doi.org/10.1155/2012/437912. [18]全卫贞,王志华.二阶非线性差分方程xn+1=f(xn,xn-1)的正解收敛性[J].四川师范大学学报:自然科学版,2012,35(1):68-72. [19]李思霖.广义Rosenau-Burgers方程的有限差分近似解[J].四川师范大学学报:自然科学版,2013,36(4):595-598. [20]Atici F M,Cabada A.Existence and uniqueness results for discrete second order periodic boundary value problem[J].Comput Math Appl,2003,45:1417-1427. [21]Merdivenci F.Two positive solutions of a boundary value problem for diference equations[J].J Difference Equ Appl,1995,1:262-270. [22]郑茂波,胡劲松,胡兵.正则长波方程的一个新的差分逼近[J].四川师范大学学报:自然科学版,2011,35(3):305-308.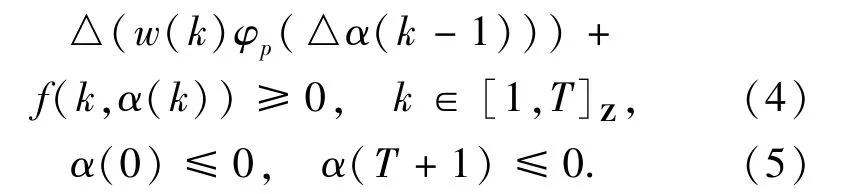


2 主要定理及其证明