几乎经典素子模

卢小往

(1.兰州理工大学 理学院，甘肃 兰州 730050；2.淮安市楚州中学，江苏 淮安 223200)

1 引言

素子模是素理想的推广,最近几年许多学者对素子模做了大量的研究[1～8].文献[1]给出了素子模的概念并讨论了其性质.文献[2]对素子模做了推广,给出弱素子模的概念及其性质.文献[3]又将弱素子模推广到几乎素子模,指出素子模是几乎素子模但反之未必.另一方面,文献[4]引入了经典素子模,并且指出经典素子模比素子模更自然.受其启发本文引入几乎经典素子模,并研究其性质.

本文中的环R指含幺交换环,所涉及的模均为左R-模.设M是R-模，N是M的真子模；I是环R的真理想，a∈R.记

(N∶M)={r∈R|rM⊆N}，(N∶I)={m∈M|Im⊆N}，(N∶a)={m∈M|am∈N}.

称I为弱素理想[5],如果对任意a,b∈R且满足0≠ab∈I,有a∈I或b∈I;称I为几乎素理想[6],如果对任意a,b∈R且满足ab∈II2,有a∈I或b∈I.称N为素子模[1],如果对任意a∈R,m∈M且满足am∈N,有m∈N或a∈(N∶M)；称N为几乎素子模[3],如果对任意a∈R,m∈M且满足am∈N(N∶M)N,有m∈N或a∈(N∶M);称N为经典素子模[4],如果对任意a,b∈R,m∈M且满足abm∈N, 有am∈N或bm∈N;称N为弱素子模[2],如果对任意a∈R,m∈M且满足0≠am∈N,有m∈M或a∈(N∶M);称N为弱经典素子模[7],如果对任意a,b∈R,m∈M且满足0≠abm∈N,有am∈N或bm∈N.

2 主要结果

定义1 称M的真子模N为几乎经典素子模,如果对任意a,b∈R,m∈M且满足abm∈N(N∶M)N,有am∈N或bm∈N.

定理1 设M是R-模,N是M的真子模, 则下列各款等价：

(1)N是几乎经典素子模.

(2) 对任意a,b∈R,有(N∶ab)=((N∶M)N∶ab)∪(N∶a)∪(N∶b).

(3) 若a∈R和m∈M满足am∉N，则(N∶am)=((N∶M)N∶am)∪(N∶m).

(4) 若a∈R和m∈M满足am∉N,则(N∶am)=((N∶M)N∶am)，或(N∶am)=(N∶m).

(5) 若a∈R，R的理想I和m∈M满足aIm⊆N(N∶M)N,则am∈N或Im⊆N.

(6) 对R的任意理想I和任意a∈R,有(N∶aI)=((N∶M)N∶aI)∪(N∶a)∪(N∶I).

(7) 若R的理想I和m∈M满足ImN,则(N∶Im)=((N∶M)N∶Im)∪(N∶m).

(8) 若R的理想I和m∈M满足ImN,则(N∶Im)=((N∶M)N∶Im)或(N∶Im)=(N∶m).

(9) 若R的理想I,J和m∈M满足IJm⊆N(N∶M)N,则Im⊆N或者Jm⊆N.

证明(1)⟹(2) 设m∈(N∶ab)，则abm∈N.如果abm∈(N∶M)N,则m∈((N∶M)N∶ab).若abm∉(N∶M)N,则am∈N或bm∈N,即m∈(N∶a)或m∈(N∶b),从而(N∶ab)⊆((N∶M)N∶ab)∪(N∶a)∪(N∶b).反过来的包含关系是显然的.

(2)⟹(3) 设a∈R,m∈M，且am∉N.若x∈(N∶am)，则axm∈N.因此m∈(N∶ax).由am∉N,得m∉(N∶a).根据条件(2)，有m∈((N∶M)N∶ax)或m∈(N∶x),即x∈((N∶M)N∶am)或x∈(N∶m),从而(N∶am)⊆((N∶M)N∶am)∪(N∶m).反过来的包含关系是显然的.

(3)⟹(4) 根据“如果一个理想等于两个理想之并，则这个理想等于其中一个理想”可得.

(4)⟹(5) 设aIm⊆N(N∶M)N，则I⊆(N∶am)且I⊄((N∶M)N∶am).如果am∈N，则结论成立.如果am∉N，则根据条件(4)得I⊆(N∶m),即Im⊆N.

(5)⟹(6) 设m∈(N∶aI)，则aIm⊆(N∶M)N,于是m∈((N∶M)N∶aI).若aIm⊄(N∶M)N,则am∈N或者Im⊆N，即m∈(N∶I),从而(N∶aI)⊆((N∶M)N∶aI)∪(N∶a)∪(N∶I).而反过来包含关系是显然的.

(7)⟹(8) 与(3)⟹(4)同理.

(8)⟹(9) 设IJm∈N(N∶M)N,则J⊆(N∶Im)且J((N∶M)N∶Im).如果Im⊆N，则结论成立.如果ImN,则根据条件(8)得J⊆(N∶m),即Jm⊆N.

(9)⟹(1) 设abm∈N(N∶M)N,得(a)(b)m⊆N(N∶M)N.由条件(9)得(a)m⊆N或者(b)m⊆N,从而am∈bm∈N.故N是几乎经典素子模.

定理2 设M是R-模，N是M的子模，则有：

(1) 如果N是M的几乎经典素子模，则对任意a,b∈R,m∈M且满足abm∈N(N∶M)N，有am∈N或bm∈N或ab∈(N∶M).

(2) 若(N∶M)是几乎素理想，如果对任意a,b∈R,m∈M满足条件abm∈N(N∶M)N，有am∈N或bm∈N或ab∈(N∶M)，则N是M的几乎经典素子模.

证明(1) 显然.

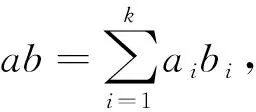
定理3 设M是R-模，N是M的真子模，则N是M的几乎经典素子模当且仅当N/(N∶M)N是M/(N∶M)N的弱经典素子模.

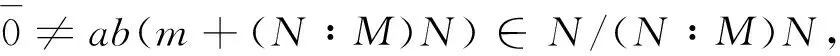
定理4 设K是M的子模且K⊆(N∶M)N，则N是M的几乎经典素子模当且仅当N/K是M/K的几乎经典素子模.

证明必要性.设a,b∈R,m+K∈M/K满足ab(m+K)∈N/K-(N/K∶M/K)(N/K),则abm+K∈N/K-(N∶M)(N/K),因此abm∈N(N∶M)N.因为N是M的几乎经典素子模，所以am∈N或者bm∈N,从而a(m+K)∈N/K或者b(m+K)∈N/K.故N/K是M/K的几乎经典素子模.

充分性.设a,b∈R,m∈M满足abm∈N(N∶M)N,则由K⊆(N∶M)N⊆M得abm+K∈N/K-(N∶M)(N/K),即ab(m+K)∈N/K-(N/K∶M/K)(N/K).由于N/K是M/K的几乎经典素子模，所以a(m+K)∈N/K或者b(m+K)∈N/K.所以am∈N或者bm∈N.故N是M的几乎经典素子模.

下述定理表明几乎经典素子模对于局部化运算是封闭的.

定理5 设N是M的几乎经典素子模，S是R的乘法闭子集且满足(N∶M)∩S=Ø，则S-1N是S-1M的几乎经典素子模.

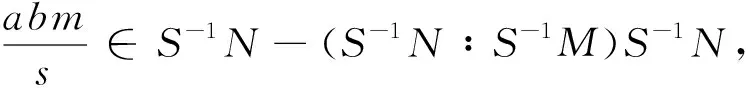
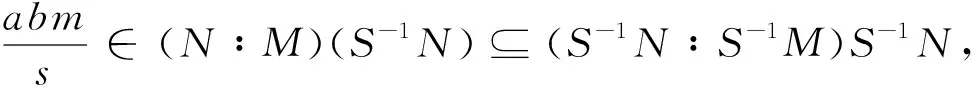
下面考虑几乎素子模与几乎经典素子模的关系.

定理6 设M是R-模，则有：

(1)M的几乎素子模都是几乎经典素子模.

(2) 若M是循环模，则M的几乎经典素子模都是几乎素子模.

证明(1) 设N是M的几乎素子模，a,b∈R和m∈M满足abm∈N(N∶M)N，则有a∈(N∶M)或bm∈N，进而am∈N或bm∈N.所以N是M的几乎经典素子模.

(2) 设M=Rm，N是M的几乎经典素子模.若r∈R和x∈M满足rx∈N(N∶M)N，令x=sm，其中s∈R，则有rx=rsm∈N(N∶M)N.由于N是M的几乎经典素子模，故有rm∈N或sm∈N，从而rM⊆N或x∈N.所以N是M的几乎素子模.

例1 设R=,M=p⊕⊕,其中p是素数.考虑.

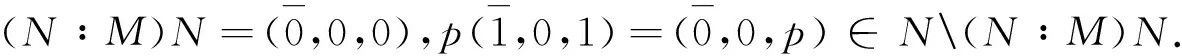
我们说明N是M的几乎经典素子模.设m,n,z,w∈,p满足则故p|mnx,z=0，所以p|m或p|nx.如果p|m,则如果p|nx,则因此N是M的几乎经典素子模.

下面考虑几乎经典素子模与模的直和的关系.

定理7 设M1,M2是R-模，N1是M1的真子模，则下列条件等价：

(1)N=N1⊕M2是M=M1⊕M2的几乎经典素子模.

(2)N1是M1的几乎经典素子模，且对每个r,s∈R,m1∈M1有，若rsm1∈(N∶M)N1,rm1∉N1,sm1∉N1则rs∈((N∶M)M2∶M2).

证明(1)⟹(2)设N=N1⊕M2是M=M1⊕M2的几乎经典素子模.又设r,s∈R,m1∈M1满足rsm1∈N1(N1∶M1)N1，则rs(m1,0)∈N1⊕M2(N1⊕M2)即rs(m1,0)∈N(N∶M)N.因此r(m1,0)∈N或者s(m1,0)∈N,从而rm1∈N1或者sm1∈N1,由此可得N1是M1的几乎经典素子模.假设rs∉((N∶M)M2∶M2),则存在m2∈M2使得rsm2∉(N∶M)M2,从而rs(m1,m2)∈N(N∶M)N,因此r(m1,m2)∈N或者s(m1,m2)∈N,从而rm1∈N1或者sm1∈N1，矛盾.故rs∈((N∶M)M2∶M2).

(2)⟹(1)设r,s∈R,(m1,m2)∈M=M1⊕M2.又设rs(m1,m2)∈N(N∶M)N.如果rsm1∈N1(N1∶M1)N1,则根据(2)得，rm1∈N1,所以r(m1,m2)∈N或者s(m1,m2)∈N.如果rsm1∈(N1∶M1)N1,则rsm2∉(N∶M)M2,从而rs∉((N∶M)M2∶M2).由(2)得rm1∈N1或者sm1∈N1,所以r(m1,m2)∈N或者s(m1,m2)∈N.所以N=N1⊕M2是M=M1⊕M2的几乎经典素子模.

定理8 设M1,M2是R模，N1,N2分别是M1,M2的真子模.如果N=N1⊕N2是M=M1⊕M2的几乎经典素子模，则Ni是Mi的几乎经典素子模,i=1,2.

证明设r,s∈R,m1∈M1满足rsm1∈N1(N1∶M1)N1，则rs(m1,0)∈(N1⊕N2)(N1⊕N2∶M1⊕M2)(N1⊕N2),由N=N1⊕N2是M=M1⊕M2的几乎经典素子模得，r(m1,0)∈N1⊕N2或者s(m1,0)∈N1⊕N2,从而rm1∈N1或者sm1∈N1.所以N1是M1的几乎经典素子模.同理N2是M2的几乎经典素子模.