度量空间中的Edelstein-Suzuki型随机不动点定理

陈永亮, 韩晓玲

(西北师范大学数学与统计学院,甘肃兰州730070)

1 引言及预备知识

随机不动点理论在各类随机微分积分方程的研究中起着重要作用,文献[1]将Banach压缩原理随机化,得到了随机压缩映射不动点定理;A.T.Bharucha Reid[2]将著名的Schauder不动点定理随机化,建立了随机Schauder不动点定理;张石生[3]建立了一系列随机压缩映像不动点定理;李国祯[4]将Leray-Schauder拓扑度和不动点指数理论随机化,建立了随机拓扑度和指数理论;上述不动点定理都有着广泛的应用.

近年来,许多学者不断的将Banach压缩原理进行改进,得到了各种形式的压缩不动点定理[5-10].本文将文献[5]中的不动点定理随机化,得到了一个新的随机不动点定理.

本文假设(Ω,Σ,μ)为一完备的概率测度空间,E为可分的实Banach空间,(E,B)为可测空间,其中,B为E的一切Borel子集的σ-代数.

定义1.1[11]映像x:Ω➝E称为E-值Σ-可测,若对E中的任意开集S,集合{ω∈Ω|x(ω)∈S}∈Σ.

定义1.2[11]算子A:Ω×E➝E称为随机算子,若对∀x∈E,A(ω,x)为E-值随机变量,即对E中任意闭集S,集合{ω∈Ω|A(ω,x)}∈Σ.特别地,若算子A(ω):E➝E对∀x∈E,A(ω)x为E-值随机变量,则A(ω)为随机算子.

定义 1.3[12]设A(ω)为随机算子,若存在E-值随机变量x(ω),使得A(ω)x(ω)=x(ω),∀ω∈Ω,则称x(ω)为算子A(ω)的随机不动点.

定义1.4[10]设θ是E的零元素,P是E中的一个集合,intP表示P的内部.集合P被称为一个锥,如果:

(a)P是非空的闭集且P≠{θ};

(b)a,b∈R,a,b≥0,x,y∈P⇒ax+by∈P;

(c)P∩(-P)={θ}.

对于给定的锥P,可以通过如下方法在P上定义偏序关系≼,x≼y当且仅当y-x∈P.x≺y表示x≼y且x≠y.x≪y表示intP.如果P非空,则称P为体锥.

定义1.5[10]锥P⊂E称为正规锥,如果∃K>0使得对所有的x,y∈E,

定义1.6[10]设X是一个非空集,映射d:X×X➝E,其中d满足:

(i)θ≼d(x,y),∀x,y∈X,d(x,y)=0,当且仅当x=y;

(ii)d(x,y)=d(y,x),∀x,y∈X;

(iii)d(x,y)≼d(x,z)+d(z,y),∀x,y,z∈X,则称d是X上的一个度量,(X,d)是一个抽象的度量空间.

引理1.1[10]若P是E中的一个正规锥,则∃E的一个单调范数‖·‖1,即∀x,y∈E,

如果P还是一个体锥,则有

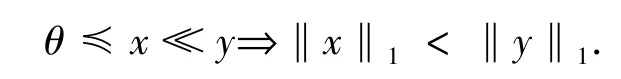
2 主要结果和证明

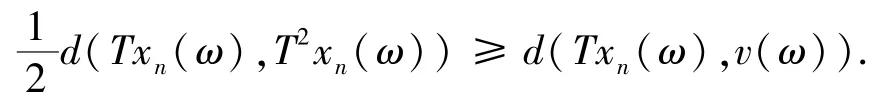
显然,对一些n∈N,上面2个不等式不能同时成立,即对每一个n∈N必有以下2种情形之一成立:

若(2)式成立时,可以得到若(3)式成立时,可以得到

显然,能使得以上2个不等式之一成立的n构成N中的一个无限集.如果能使不等式(2)成立的n构成无限集N1∈N,则取极限,当N1∋n➝∞可得

不等式(3)成立的情形与不等式(2)的证明类似,因此,无论那一种情形都可以得到

这与假设没有随机不动点矛盾.

假设v(ω)是T(ω)的一个随机不动点,u(ω)是T(ω)的另一个随机不动点,v(ω)∈X;u(ω)∈X,v(ω)≠u(ω).因

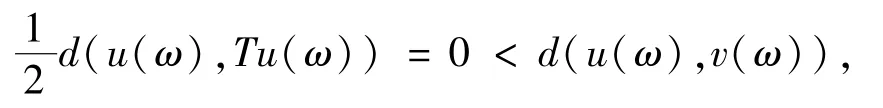
根据(1)式可得

如果E≤B+C+D,则A+D+E≤A+B+C+2D=1,这就与d(u(ω),v(ω))>0矛盾.证毕.

如果取A=1和B=C=D=E=0,可以获得随机化了的Suzuki不动点定理.

推论2.2设(X,d)是一个紧的度量空间,随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,∀ω∈Ω有

则T(ω)在X中有唯一的随机不动点.

如果取A=D=E=0和B+C=1,B≠0,可以得到随机化了的Kannan不动点定理.

推论2.3设(X,d)是一个紧的度量空间,随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,∀ω∈Ω有

其中,B、C是非负常数,满足B+C=1,C≠1,则T(ω)在X中有唯一的随机不动点.

如果取A=B=C=0和D=1/2,可以得到随机化了的Chatterjea不动点定理.

推论2.4设(X,d)是一个紧的度量空间,随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,∀ω∈Ω有

其中,E是任意固定的非负常数,则T(ω)在X中有随机不动点.如果,则不动点是唯一的.

定理2.5设(X,d)是锥P上一个紧的锥度量空间,其中,P是正规的体锥.随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,x(ω)≠y(ω),∀ω∈Ω有

则T(ω)在X中有唯一随机不动点.

证明因为P是一个正规的体锥,由引理1.1得,存在E的一个单调范数‖·‖1,即

则D是一个实值度量,(X,D)是一个紧的度量空间.这样就把原问题等价的转化为证明推论2.2的条件,即对任意可测的随机变量x(ω),y(ω)∈X,∀ω∈Ω有

这就与假设矛盾.因此可得

根据范数的单调性可得

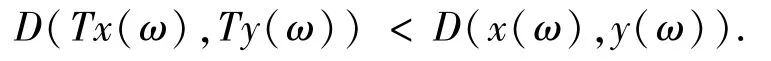
由推论2.2可得T(ω)在X中有一个随机不动点.

定理2.6设(X,d)是锥P上一个紧的锥度量空间,其中,P是正规的体锥.随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,x(ω)≠y(ω),∀ω∈Ω有

其中,A、B、C、D、E是非负常数,满足:A+B+C+2D=1且C≠1,则T(ω)在X中有一个随机不动点,进一步假设E≤B+C+D则不动点是唯一的.

推论2.7设(X,d)是锥P上一个紧的锥度量空间,其中,P是正规的体锥.随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,x(ω)≠y(ω),∀ω∈Ω有

其中,B、C是非负常数,满足B+C=1,C≠1,则T(ω)在X中有唯一的随机不动点.

推论2.8设(X,d)是锥P上一个紧的锥度量空间,其中,P是正规的体锥.随机算子T:Ω×X➝X,假设对任意可测的随机变量x(ω),y(ω)∈X,x(ω)≠y(ω),∀ω∈Ω有

则T(ω)在X中有唯一的随机不动点.

[1]Hans O.Random operator equations[C]//Proc 4th Berkekey Symp-Math Statist and Probability.Berkekey:Univ California Press,1960(2):185-202.

[2]Bharucha Ried A T.Fixed point theorems in probabilistic analysis[J].Bull Am Math Soc,1976,82(5):641-657.

[3]张石生.不动点理论及其应用[M].重庆:重庆出版社,1984:1-99.

[4]李国祯.随机1-集压缩算子的随机不动点指数和随机不动点定理[J].应用数学学报,1996,19(2):203-212.

[5]Doric D,Kkadelburg Z,Radenovic S.Edelstein-Suzuki-type fixed point results in metric and abstract metric spaces[J].Nonlinear Anal:TMA,2012,75:1927-1932.

[6]Suzuki T.A generalized Banach contraction principle that characterizes metric completeness[J].Proc Am Math Soc,2008,136:1861-1869.

[7]Edelstein M.On fixed and periodic points under contractive mappings[J].J London Math Soc,1962,37:74-79.

[8]Kikkawa M,Suzuki T.Three fixed point theorems for generalized contractions with constants in complete metric spaces[J].Nonlinear Anal,2008,69:2942-2949.

[9]Popescu O.Two fixed point theorems for generalized contractions with constants in complete metric spaces[J].Cent Eur J Math,2009(7):529-538.

[10]Suzuki T.A new type of fixed point theorem in metric spaces[J].Nonlinear Anal:TMA,2009,71:5313-5317.

[11]王梓坤.随机泛函分析引论[J].数学进展,1962(5):45-71.

[12]丁协平.连续随机算子的不动点定理[J].数学进展,1983,12:294-298.

[13]Itoh S.Random fixed point theorems with an application to random differential equations in Banach spaces[J].J Math Anal Appl,1979,67:261-273.

[14]Itoh S.A random fixed point theorem for a multivalued contraction mapping[J].Pacific J Math,1977,68:85-90.

[15]杨庚华,李国祯.Altman定理在随机集值半闭1-集压缩映像下的推广[J].四川师范大学学报:自然科学版,2010,33(2):203-205.

[16]汪春阳.一类广义随机非线性隐变分不等式组[J].四川师范大学学报:自然科学版,2008,31(5):505-507.

[17]刘春晗,李娜,王鑫.局部凸拓扑空间中凝聚映象的不动点定理[J].四川师范大学学报:自然科学版,2012,35(5):625-627.

[18]夏顺友.抽象凸锥度量空间上集值映射的逼近连续选择及应用[J].四川师范大学学报:自然科学版,2013,36(4):521-524.

[19]李志龙.不连续随机算子随机不动点定理及其应用[J].数学物理学报,2010,A30(2):542-547.

[20]张宪.序压缩映射的不动点定理[J].数学学报,2005,48(5):973-978.