奇异三阶三点边值问题正解的存在性

何文魁

(西北师范大学数学与统计学院,甘肃兰州730070)

1 引言及预备知识

近年来,基于具体的应用背景,对奇异边值问题正解存在性的研究吸引了许多学者的广泛关注,并且得到了许多结果[1-7],关于更多三阶边值问题的结果,参见文献[8-12].

2011年,文献[1]获得了

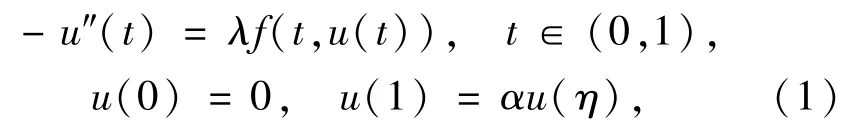
2个正解的存在性结果,其中,λ>0为参数,α∈[0,1),η∈(0,1),f∈C((0,1) ×(0,+∞),[0,+∞)),且在t=0、t=1和u=0处有奇性.

2010年,文献[2]研究了

正解的存在性和不存在性,其中,1/2

2005年,文献[3]获得了

一个及多个正解的存在性结果,其中,1/2≤η<1为固定常数,a∈C((0,1),[0,+∞)),且在t=0和t=1处有奇性,F∈C([0,1]×[0,+∞),[0,+∞)).

在上述假设条件下,文献[3]得到定理A.

定理A假设(A1)和(A2)成立,且有F0=F0=F∞=F∞=+∞,则∃λ∗使得对∀λ∈n(0,λ∗),问题(3)至少存在2个正解,其中

受上述文献的启发,本文考虑

正解的存在性,其中,λ>0为参数,1/2

类似于文献[1]二阶方程的情形,本文得到了三阶边值问题(4)2个正解的存在性结果,和文献[2-3]相比较,在允许g和f分别在t=0、t=1和u=0处有奇性的情形下考虑问题(4)正解的存在性,而在文献[2]中,g和f都没有奇性,文献[3]只允许a(t)在t=0和t=1有奇性,因此,考虑的情形较文献[2-3]更为广泛,得到的结果比定理A更加深刻;另外,由u(p)-u(1)=0得到,∃η∈(p,1)使得u′(η)=0,因此,边界条件u(0)=u(p)-u(1)=u″(1)=0 蕴含u(0)=u′(η)=u″(1)=0,若令p➝1-,则边界条件u(0)=u(p)-u(1)=u″(1)=0 可退化为u(0)=u′(1)=u″(1)=0,从而,我们的问题更具一般性,研究其正解的存在性是必要的.

令X=C[0,1],其上范数为,x∈X,则X按上述范数构成Banach空间.

引理1.1[2]对∀h∈C[0,1],线性问题

为区间[a,b]上的特征函数,并且G(t,s)≥0,(t,s)∈[0,1]2.

引理1.2[2]若u∈C3[0,1],且满足

并且a(t)≥min{t,1-t}≥t(1-t),0≤t≤1.

引理1.3[13-14]设X为实Banach空间,K⊂X为锥,Ω⊂X为有界开集,θ∈Ω是X中的零元,算子T:K∩|➝K全连续,

(i)若x≠μTx对∀x∈K∩∂Ω和μ∈[0,1]成立,则i(T,K∩Ω,K)=1;

(ii) 若∃θ≠x0∈K,使得x≠Tx+tx0对∀x∈K∩∂Ω成立,则i(T,K∩Ω,K)=0.

引理1.4[4]若f∈C((0,+∞),[0,+∞)),则存在单调增函数h∈C([0,+∞),[0,+∞)),使得f·h∈C([0,+∞),[0,+∞)),且满足h(t)>0于(0,+∞).

2 主要结果及证明

定理2.1假设(H1)和(H2)成立,则∃λ∗>0,对∀λ∈(0,λ∗),问题(4)至少存在2个正解u和v,满足0<‖u‖

为了证明定理2.1,首先考虑辅助问题

定义算子Tn:K|➝C+[0,1]如下

其中,C+[0,1]={u∈X|u(t)≥0,t∈[0,1]},由引理1.2,TK⊂K,类似文献[3]的引理2.3,可以证明Tn:K|➝K全连续,由引理1.1,辅助问题(5)的解等价于u=λTnu的不动点.

引理 2.1对 ∀r>0,∃λr>0,使得i(λTn,Kr,K)=1对∀λ∈(0,λr)和n∈N 成立,其中,Kr={u∈K|‖u‖

证明由引理1.4,存在单调增函数h∈C([0,+∞),[0,+∞))使得f·h∈C([0,+∞),[0,+∞)),且满足h(t)>0于(0,+∞),对∀r>0,令

[1]Li Y,Liang Z P.Two positive solutions to three-point singular boundary value problems[J].Acta Math Sci,2011,B31(1):29-38.

[2]Graef J R,Kong L J,Yang B.Positive solutions to a nonlinear third-order three-point boundary value problem[J].Electric J Diff Eqns,2010,19:151-159.

[3]Sun Y P.Positive solutions of singular third-order three-point boundary value problem[J].J Math Anal Appl,2005,306:589-603.

[4]Liu Y.Twin solutions to singular semipositone problems[J].J Math Anal Appl,2003,286:248-260.

[5]Agarwal R P,O’Regan D.Nonlinear superlinear singular and nonsingular second order boundary value problems[J].J Diff Eqns,1998,143:60-95.

[6]Li S H.Poitive solutions of nonlinear singular third-order two-point boundary value problem[J].J Math Anal Appl,2006,323:413-425.

[7]Yao Q L.Positive solutions of singular third-order three-point boundary value problems[J].J Math Anal Appl,2009,354:207-212.

[8]Ma R Y.μltiplicity results for a third-order boundary value problem at resonance[J].Nonlinear Anal,1998,32:493-499.

[9]Anderson D,Avery R I.Multiple positive solutions to a third-order discrete focal boundary value problem[J].Comput Math Appl,2001,42:333-340.

[10]Anderson D R,Davis J M.Multiple solutions and eigenvalues for third-order right focal boundary value problems[J].J Math Anal Appl,2002,267:135-157.

[11]Graef J R,Yang B.Positive solutions for a third-order nonlocal boundary value problem[J].Discrete Cont Dyn Syst,2008(S1):89-97.

[12]Graef J R,Yang B.Positive solutions of a third-order eigenvalue problem[J].Dyn Syst Appl,2006,15:97-110.

[13]Deimling K.Nonlinear Functional Analysis[M].Berlin:Springer-Verlag,1985.

[14]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,2001.

[15]Ma R Y.Existence theorems for a second order three-point boundary value problem[J].J Math Anal Appl,1997,212:430-442.