四阶时滞微分方程边值问题的正解

汪媛媛, 李永祥

(西北师范大学数学与统计学院,甘肃兰州730070)

1 引言及预备知识

记C=C([-τ,0],R),则其按范数构成 Banach 空间.令C+={φ∈C|φ(θ)≥0,θ∈[-τ,0]}.考虑四阶时滞微分方程边值问题

正解的存在性,其中,f:I×C+➝[0,+∞)连续,I=[0,1],ϕ(t)∈C([-τ,0],[0,+∞)),ϕ(0)=0,对∀t∈I,ut(θ)=u(t+θ),θ∈[-τ,0],

本文始终假设:

两端简单支撑的弯曲弹性梁的平衡状态可用四阶边值问题

来描述[1-2],其中,f:[0,1]×R×R➝R连续,关于边值问题(2)以及更广泛的常微分方程边值问题解的存在性,已有许多研究工作[3-11].近年来,伴随着时滞微分方程理论的发展以及其在物理学、自动控制理论、生物学、经济学、人口理论等多门学科中的广泛应用,时滞微分方程边值问题已逐渐成为一个研究的热点[12-25].

对不含时滞的情形,即τ=0时,问题(1)退化为下面的常微分方程边值问题

其中,f:I×[0,+∞)➝[0,+∞)连续.问题(3)已被许多作者研究[3-6],其中,文献[3]给出了其正解的存在性定理.

对含有时滞项的情形,即τ≠0时,宋利梅等在文献[12]中讨论了边值问题

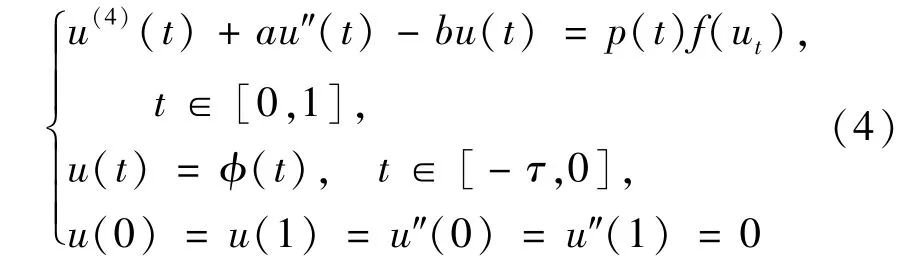
正解的存在性,其中,f是定义在I×C+上的非负连续函数,p(t)是定义在I上的非负可测函数.他们运用锥拉升与锥压缩不动点定理证明了问题(4)正解的存在性.

本文考虑更一般的四阶时滞微分方程边值问题(1).通过对不动点指数的精确计算,证明了只要f0适当小,f∞适当大,或者f0适当大,f∞适当小时,问题(1)至少存在一个正解.

称u(t)∈C4[-τ,1]为问题(1)的一个解,如果u(t)满足下面的条件:

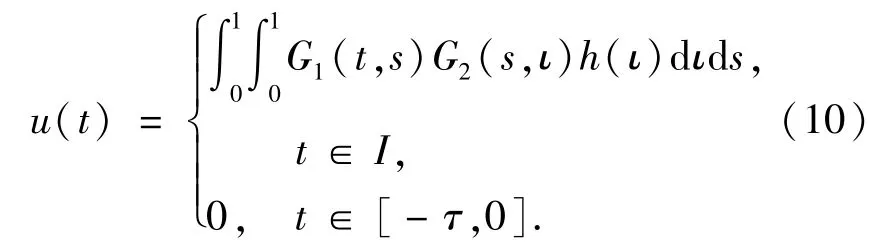
定义线性算子T:C[-τ,1]➝C[-τ,1]为

则算子T是方程(9)的解算子,且T把C[-τ,1]中的有界集映为C[-τ,1]中的有界集.由Gelfand公式得

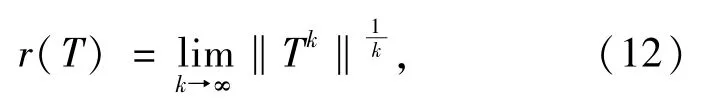
其中,r(T)是算子T的谱半径,显然r(T)>0.设L=π4-aπ2-b,易见L是线性边值问题(9)对应的最小特征值,因此r(T)=1/L.

引理3T是全连续算子.

证明T的连续性显然,只需证明T的等度连续性即可.

由于G1和G2在[0,1]×[0,1]一致连续,即对∀ε>0,∃η>0,∀t1,t2∈[0,1],当|t1-t2|<η时有

联立以上两式可得

又因为当t∈[-τ,0]时,Au(t)=0;当t∈(0,1)时,Au(t)>0,从而可得A(K)⊂K.由T的全连续性可知A是全连续的.证毕.

引理 5[9]∃γ∈(0,1),使得对∀x∈K,当t∈时,有‖xt‖C≥γ‖x‖.

引理6[3]设A:K➝K全连续,如果μAu≠u,∀u∈∂Kr1,且0<μ≤1时,i(A,Kr1,K)=1,其中,Kr1={u∈K|‖u‖C

引理7[3]设A:K➝K全连续,如果下列条件满足:

则i(A,KR,K)=0,其中,KR={u∈K|‖u‖C

2 主要结果

定理1f是定义在I×C+上的非负连续函数,且f把I×C+中的有界集映为[0,+∞)中的有界集,如果下列条件之一满足:

则边值问题(1)至少存在一个正解.

证明假设条件(H1)成立,则由ϕ(t)≡0,得vt=0,t∈[0,1].

由(H1)的第一个不等式,因为f0<δL,则存在适当的r0,满足0

下证当0<μ≤1时,对∀x∈∂Kr0,有μAx≠x.反设∃x0∈∀Kr0,μ0∈(0,1],使得μ0Ax0=x0,则由A的定义,x0满足

[1]Gupta C P.Existence and uniqueness results for the bending of an elastic beam equation at resonance[J].J Math Anal Appl,1988,135:208-225.

[2]Gupta C P.Existence and uniqueness theorems for a bending of an elastic beam equation[J].Appl Anal,1988,26:289-304.

[3]Li Y.Positive solutions of fourth-order boundary value problems with two parameters[J].J Math Anal Appl,2003,281:477-484.

[4]李永祥.四阶非线性边值问题解的存在性与上下解方法[J].数学物理学报,2003,A23(2):245-252.

[5]李永祥,杨和.用椭圆描述的四阶边值问题的两参数非共振条件[J].数学物理学报,2010,A30(1):239-244.

[6]黄永峰.一类带参数的四阶两点边值问题正解的存在性[J].长江大学学报:自然科学版,2011,8(9):1-3.

[7]王珍燕.带2个参数四阶边值问题的正解及多个正解的存在性[J].烟台大学学报:自然科学版,2012,25(1):9-15.

[8]Ma R.Existence of positive solutions of a fourth-order boundary value problem[J].Appl Math Comput,2005,168:1219-1231.

[9]Ma R.Positive solutions for boundary value problems of functional differential equations[J].Appl Math Comput,2007,193:66-72.

[10]Pang C C,Dong W,Wei Z L.Multiple soluttions for fourth-order boundary value problem[J].J Math Anal Appl,2006,314:464-476.

[11]Jiang D,Liu H,Xu X.Nonresonant singgular fourth-order boundary value problems[J].Appl Math Lett,2005,18:69-75.

[12]宋利梅,翁佩萱.四阶泛函微分方程边值问题正解的存在性[J].高校应用数学学报,2011,26(1):67-77.

[13]宋常修,翁佩萱.四阶非线性泛函微分方程边值问题的正解[J].华南理工大学学报:自然科学版,2006,34(7):128-132.

[14]夏青.一类二阶时滞微分方程的边值问题[J].中国海洋大学学报,2007,20:127-130.

[15]王洁,刘斌.二阶时滞微分方程边值问题正解的存在性[J].应用数学,2007,20:127-130.

[16]王宏洲.二阶时滞微分方程边值问题的上下解方法[J].数学学报,2010,53(3):489-494.

[17]Weng P.Monotone method for fourth-order boundary value problems of functional differential equations[J].Comput Math Appl,1993,37:1-9.

[18]Weng P,Jiang D.Existence of positive solutions for boundary value problem of second-order FDE[J].Nonlinear Anal,2008,68:3646-3656.

[19]Bai D,Xu Y.Positive solutions and eigenvalue intervals of nonlocal boundary value problems with delays[J].J Math Anal Appl,2007,334:1152-1166.

[20]Gao C,Cuo Z.Existence of multiple periodic solutions foer a class of second-order delay differential equations[J].Nonlinear Anal,2009,10(5):3285-3297.

[21]Berezansky L,Diblík J.Positive solutions of second-order delay differential equations with a damping term[J].Comput Math Appl,2010,60:1332-1342.

[22]Li Y.A monotone iterative technique for solving the bending elastic beam equations[J].Appl Math Comput,2010,217:2200-2208.

[23]Yang B,Ma R,Gao C.Positive periodic solutions of delayed differential equations[J].Appl Math Comput,2011,218(8):4538-4545.

[24]Li Y.Positive periodic solutions of second-order differential equations with delays[J/OL].Abst Appl Anal,2012:2012,ID829783:13.http://www.hindawi.com/journals/aaa/2012/829783.

[25]Li Q,Li Y.On the existence of positive periodic solutions for second-order functional differential equations with multiple delays[J/OL].Abst Appl Anal,2012:2012,ID929870:13.http://www.hindawi.com/journals/aaa/2012/929870.

[26]郭大钧,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,1989.

[27]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,2002:314-315.