关于 X-Gorenstein投射模与 Y-Gorenstein内射模的余挠对
2014-08-07任兰兰杨晓燕
任兰兰, 杨晓燕
(西北师范大学数学与统计学院,甘肃兰州730070)
1 引言及预备知识
本文中的环均指有单位元的结合环,模均为酉模,所有的R-模如无特别说明均指右R-模.用Mod-R表示右R-模范畴,P( I和 F)表示投射(内射和平坦)模类,对任意的R-模M,pd(M)(id(M)和fd(M))代表模M的投射(内射和平坦)维数.若R是一个Gorenstein环,则对任意的模M,pd(M)<∞当且仅当id(M)<∞[1].设W1表示所有投射维数有限的模类.M.Hovey[2]证明了若R是一个Gorenstein环,则(W1,GI)和(GP,W1)是完备遗传的余挠对,其中GI是Gorenstein内射模类,GP是Gorenstein投射模类.若R是一个n-FC环,则对任意的模M,fd(M)<∞当且仅当FP-id(M)<∞[3].设W2表示所有平坦维数有限的模类.J.Gillespie[3]证明了若R是一个n-FC环,则(W2,DI)和( D P, W2)是完备遗传的余挠对,其中DDII是Ding-内射模类,DP是Ding-投射模类.
设X是一个包含所有投射模的模类.证明了若X是一个可解的预包络类且对任意的内射模I, X-pd(I)<∞,则(X- G P,( X- G P)⊥)是一个遗传的余挠对,其中X- G P是 X-Gorenstein投射模类.设Y是一个包含所有内射模的模类.对偶的,证明了若Y是一个余可解的预覆盖类且对任意的投射模P,Y-id(P)<∞,则(⊥(Y- G I), Y- G I)是一个遗传的余挠对,其中Y- GI是 Y-Gorenstein内射模类.
设B是一个模类,M是一个R-模.称模同态ϕ:M→B是M的一个B-预包络,其中B∈ B,如果对任意的D∈B,同态HomR(ϕ,D):HomR(B,D)→HomR(M,D)是一个满同态.称ϕ:M→B是M的一个B-包络,如果满足gϕ=ϕ的恒等自同态g:B→B是一个同构.对偶地,可以定义B-预覆盖和B-覆盖.B-包络和B-覆盖有可能不存在,如果存在,在同构的意义下是唯一的.称(A,B)是一个余挠对,如果A⊥=B且A=⊥B,其中A和B是任意的模类,,∀B∈B}.称余挠对( A, B)是遗传的,如果对任意的正合列0→A1→A2→A3→0,其中A2,A3∈A,则A1∈A;等价于,如果对任意的正合列0→B1→B2→B3→0,其中B1,B2∈B,则B3∈B.称余挠对(A,B)有足够的投射对象,如果对任意的R-模M,存在一个短正合列0→B→A→M→0,其中B∈B,A∈A.对偶地,也可定义余挠对(A,B)有足够的内射对象.称余挠对(A,B)是完备的,如果它有足够的投射和内射对象.
2 余挠理论


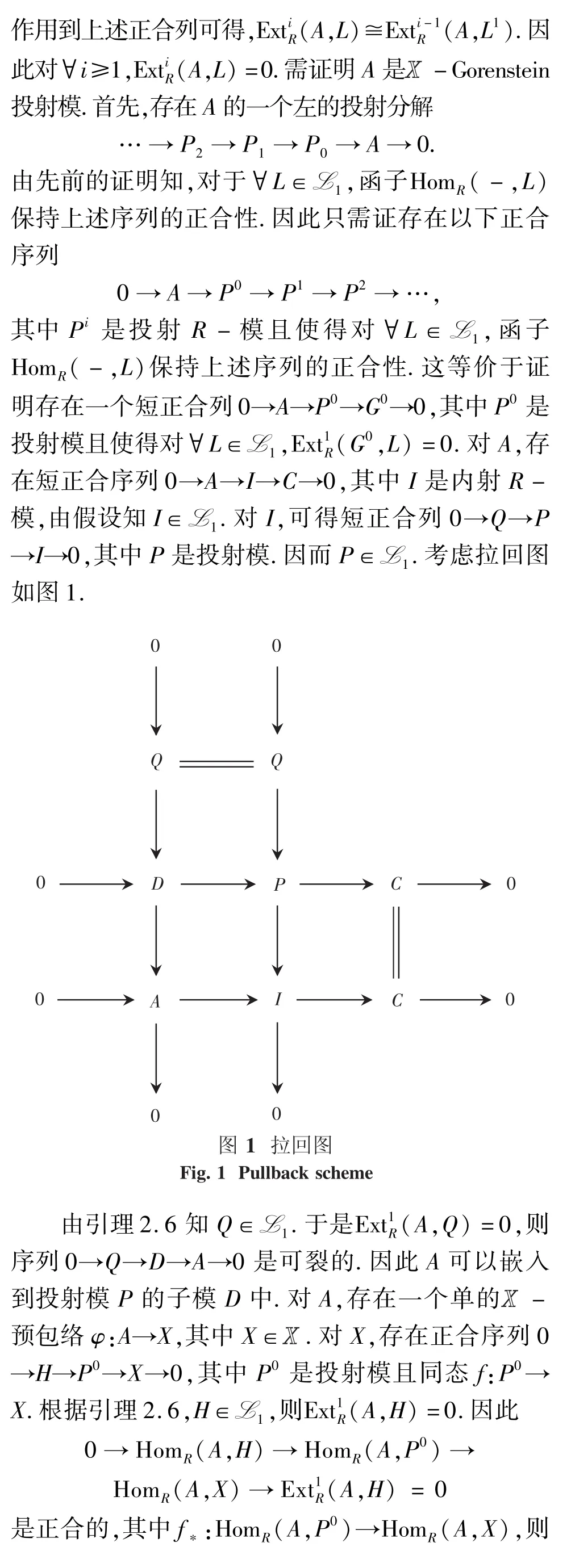


3 应用
注记3.11)设X是投射R-模的类.由文献[1]知,X-Gorenstein投射R-模类就是Gorenstein投射R-模类.用GP表示Gorenstein投射R-模的类.
2)设Y是内射R-模的类.由文献[1]知, YGorenstein内射R-模类就是Gorenstein内射R-模类.用GI表示Gorenstein内射R-模的类.
3)设X是平坦R-模的类.由文献[7]知, XGorenstein投射R-模类就是Ding-投射R-模类.用DP表示Ding-投射R-模的类.
4)设Y是FP-内射R-模的类.由文献[3]知,Y-Gorenstein内射R-模类就是Ding-内射R-模类.用DI表示Ding-内射R-模的类.
称环R是一个n-Gorenstein环,如果它是左右Noetherian环且R的左右自内射维数不超过n.称环R是一个Ding-Chen环,如果对某个n,它是一个n-FC环(即R是左右coherent环且R的左右自FP-内射维数不超过n).称环R是完全环,如果每一个R-模都有投射覆盖.对任意R-模N,其FP-内射维数定义为使得的最小的非负整数n,其中F是任意的有限表示R-模.记N的FP-内射维数为FP-id(N).若上述的n不存在,则规定FP-id(N)=∞.
命题3.2设R是左凝聚右完全环且FP-id(RR)<∞.则(GP, G P⊥)是遗传的余挠对.特别地,若R是n-Gorenstein环,则(GP, G P⊥)是完备的余挠对.
证明由文献[8]定理3.8和已知条件知,对所有的内射R-模I,pd(I)<∞.由文献[1]命题6.5.1和定理5.3.2知,若R是左凝聚右完全环,则P是预包络类.又因为P是可解的,所以由定理2.7知,(GP, G P⊥)是遗传的余挠对.特别地,若R是n-Gorenstein环,则(GP, G P⊥)是完备的余挠对.
命题3.3设R是右Noetherian环且id(RR)<∞,则(⊥GI, G I)是遗传的余挠对.特别地,若R是n-Gorenstein环,则(⊥GI, G I)是完备的余挠对.
证明因为R是右Noetherian环,所以由文献[9]命题2.2知,I是预覆盖类.对任意投射R-模P,存在自由R- 模R(Λ)使得P是R(Λ)的直和项.因为id(RR)< ∞,,所以id(P)< ∞.又因为I是余可解的,所以由定理2.12知,(⊥GI,GI)是遗传的余挠对.特别地,若R是n-Gorenstein环,则(⊥GI,GI)是完备的余挠对.
命题3.4设R是左凝聚环且FP-id(RR)<∞,则(DP, D P⊥)是遗传的余挠对.特别地,若R是Ding-Chen环,则(DP, D P⊥)是完备的余挠对.
证明由文献[1]命题6.5.1和已知条件知,F是预包络类.由文献[8]定理3.8知,若R是左凝聚环且FP-id(RR)<∞,则对所有的内射R-模I,fd(I)<∞.又F是可解的.因此由定理2.7知,( D P,D P⊥)是遗传的余挠对.特别地,若R是Ding-Chen环,则(DP, D P⊥)是完备的余挠对.
命题3.5设R是右凝聚环且FP-id(RR)<∞,则(⊥DI, D I )是遗传的余挠对.特别地,若R是Ding-Chen环,则(⊥DI, D I)是完备的余挠对.
证明因为R是右凝聚环,所以由文献[10]定理2.6知,FP-内射R-模的类是预覆盖类.由文献[8]定理3.8知,对任意投射R-模P,FP-id(P)<∞.且由文献[10]命题2.2知,FP-内射R-模类是余可解的.因此由定理2.12知,(⊥DI,DI)是遗传的余挠对.特别地,若R是Ding-Chen环,则(⊥DI,DI)是完备的余挠对.
[1]Enochs E E,Jenda O M G.Relative homological algebra[C]//De Gruyter Expositions in Math.Berlin:Walter de Gruyter&Co,2000.
[2]Hovey M.Cotorsion pairs,model category structures,and representation theory[J].Math Z,2002,241:553-592.
[3]Gillespie J.Model structures on modules over Ding-Chen rings[J].Algebra Represent Theory,2010,12:61-73.
[4]Wagstaff S S,Sharif T,White D.AB-contexts and stability for Gorenstein flat modules with respect to semidualizing modules[J].Algebra Represent Theory,2011,14:403-428.
[5]Meng F Y,Pan Q X.X-Gorenstein projective andYY-Gorenstein injective modules[J].Hacettepe Math,2011,40:537-554.
[6]Zhu X S.Resolving resolution dimension[J].Algebra Represent Theory,2013,16(4):1165-1191.
[7]Ding N Q,Li Y,Mao L X.Strongly Gorenstein flat modules[J].J Aust Math Soc,2009,66:323-338.
[8]Ding N Q,Chen J L.The flat dimensions of injective modules[J].Manuscripta Math,1993,78:165-177.
[9]Enochs E E.Injective and flat covers,envelopes and resolvents[J].Israel J Math,1981,39:190-209.
[10]Pinzon K.Absolutely pure covers[J].Commun Algebra,2008,36:2186-2194.
[11]Bennis D,Mahdou N.Global Gorenstein dimensions[J].Proc Am Math Soc,2010,138:461-465.
[12]Bennis D,Mahdou N.Gorenstein global dimensions and cotorsion dimension of rings[J].Commun Algebra,2009,37:1709-1718.
[13]Enochs E E,Oyonarte L.Covers,Envelopes and Cotorsion Theories[M].New York:Nova Science Publishers,2002.
[14]Holm H.Gorenstein homological dimensions[J].J Pure Appl Algebra,2004,189:167-193.
