单个微坑对圆锥滚子热弹流润滑的影响

2014-07-21刘昺丽王优强卢宪玖律辉

轴承 2014年10期

刘昺丽，王优强，卢宪玖，律辉

(青岛理工大学机械工程学院，山东青岛 266033)

在润滑良好的传动系统中，机械接触表面失效形式多为接触疲劳麻点。最初出现的麻点一般仅为针尖大小，如果不改善润滑环境，麻点就可能继续扩大甚至连接成片，从而造成接触表面的明显损伤[1]。宏观上，根据麻点的尺寸及形状分为初期麻点、扩展性麻点或剥落。

文中主要研究初期麻点(即非扩展性麻点)对圆锥滚子热弹流润滑的影响。利用多重网格法和多重网格积分法求得其热弹流润滑的完全数值解，分别考虑坑深、坑径、卷吸速度及载荷对油膜压力、油膜厚度及油膜中层温度的影响。

1 数学模型

圆锥滚子弹流润滑模型如图1所示(图1a和图1b分别为同向、反向圆锥滚子数学模型)[2]。A和B均为弹性圆锥滚子。如图1a建立直角坐标系，其xOy面与纸面垂直，x轴指向纸外；如图1b建立辅助坐标系y′Oz′和y″Oz″，y″通过滚子B的轴线与y″轴平行，且通过坐标原点，z′与z″轴重合，均位于滚子B的中间截面上，且都通过坐标原点。假设滚子A，B尚未修形时的素线长度均为2l，直素线段的长度为0.9×2l；两滚子的中间素线与轴线夹角分别为βa，βb；中间截面半径分别为ra，rb；小端与大端的截面半径分别为ras,ral，rbs，rbl；端部修形的圆弧半径分别为r1a,r2a,r1b,r2b。定义两滚子中间截面的当量半径r为各圆弧半径的无量纲参数，即1/r=1/ra+1/rb。

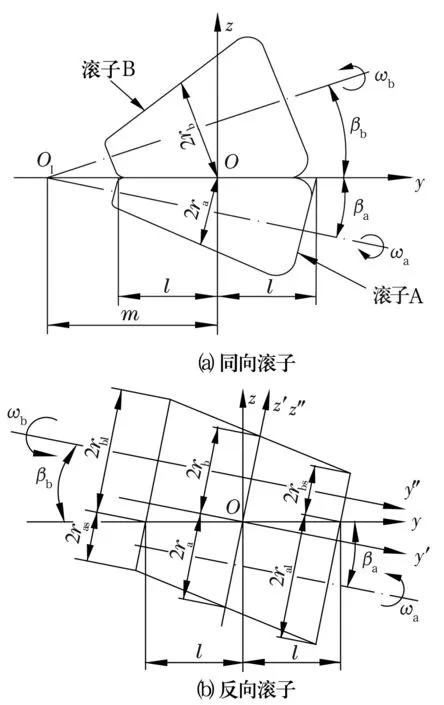
图1 圆锥滚子弹流润滑示意图

2 基本方程

假设滚子B的表面光滑，滚子A的Hertz接触区有个圆形微小凹坑。沿滚子凹坑中心处纵向剖开，如图2所示。弧线段PQR为凹坑弧长；la为凹坑的外径；θ为凹坑的弧度；Aa为凹坑深度最大值；Sa(>0)为凹坑的深度。凹坑深度的函数表达式为

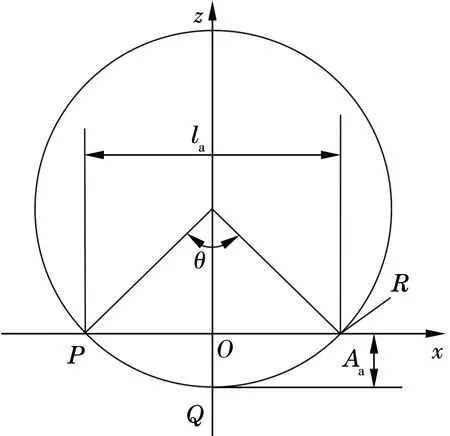
图2 凹坑示意图

(1)

2.1 Reynolds方程

考虑润滑剂为Newton流体，黏度η0和密度ρ沿膜厚方向变化的广义Reynolds方程[3]为

(2)

式中：x,y为坐标变量，m；p为油膜压力，Pa；h为油膜厚度，m；ρ为润滑油密度，kg/m3；η为润滑油黏度，Pa·s；ue为卷吸速度，且ue=(u1+u2)/2，u1，u2分别为A，B表面的速度。

2.2 考虑表面微坑的膜厚方程

考虑表面微坑的膜厚方程可表示为

h=h00+h1+h2-Sa(x,y)，

(3)

式中：h1为几何膜厚；h00，h2分别为刚体中心膜厚和法向弹性沉陷。

h1=hb-ha,

(4)

(5)

式中：x′和y′分别代表将坐标系逆时针旋转得到的新坐标系；E′为综合弹性模量。

圆锥滚子A，B在坐标系Oxyz中的曲面方程为

(6)

同向滚子时

(7)

反向滚子时

(8)

式中：当y<-0.9l时，f1=1，f2=0；当-0.9l≤y≤0.9l时，f1=f2=0；当y>0.9l时，f1=0，f2=1。

rcosβb，

racosβa，

2.3 密压与密温的关系式

润滑油密压与密温关系的经验公式为[4]

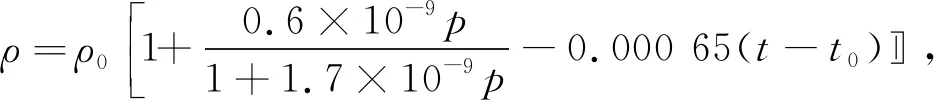
(9)

式中：ρ0为润滑油环境密度；t为润滑油温度；t0为环境温度。

计算过程中，载荷方程、黏度方程、油膜能量方程、固体能量方程及界面热连续条件可参考文献[5]。

3 基本方程的无量纲化

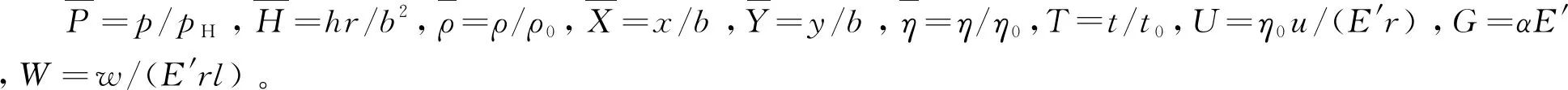
4 数据分析

压力计算采用考虑温度影响的多重网格法，膜厚计算使用多重网格积分法。以工程中常见的钢-钢接触工况为例，2个滚子的材料和几何尺寸相同，滚子A，B和所用润滑油在环境温度40 ℃(313 K)下的参数见表1。

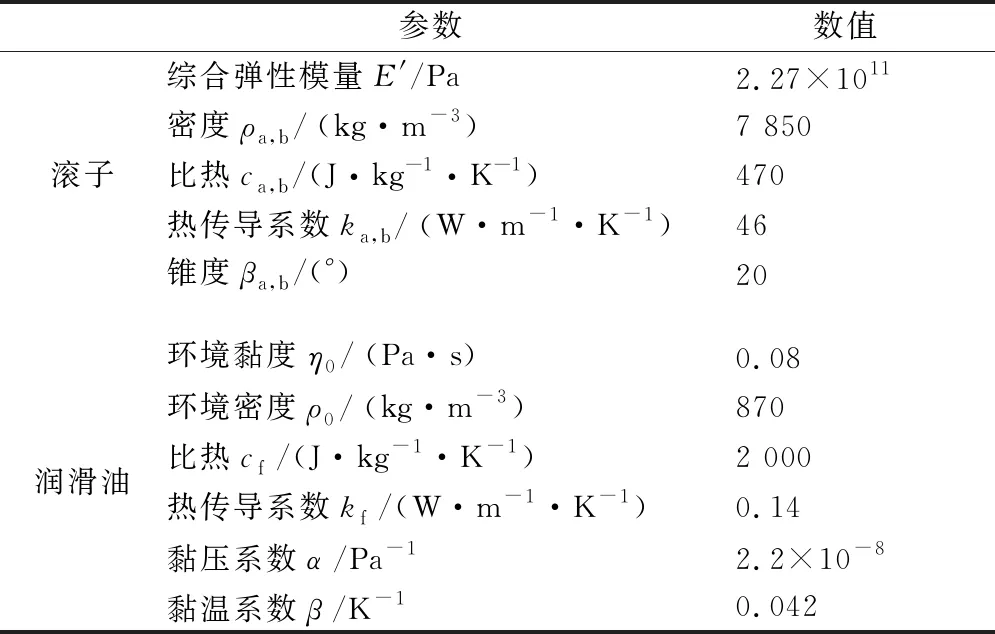
表1 润滑油和滚子的参数[6]

4.1 同向圆锥滚子模型参数分析

4.1.1 光滑及单个微坑表面的热弹流润滑结果

光滑表面与单个微坑表面热弹流润滑结果如图3所示。通过对比可知，在表面存在单个微坑的接触区域，油膜厚度在接触中部有增大现象，油膜压力在单坑区域内也有增大现象，而单个微坑对整个热弹流润滑的油膜温度影响并不明显。

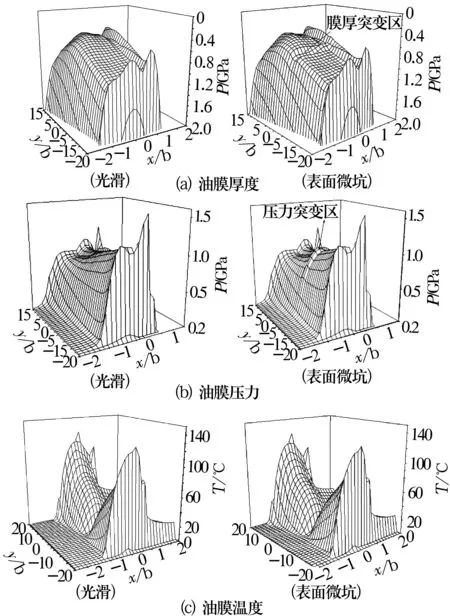
图3 光滑表面与微坑表面热弹流润滑结果

为了更清楚地看出单个微坑的影响，根据热弹流润滑结果，对比光滑表面与单个微坑表面时y=0截面上油膜厚度和油膜压力变化，如图4所示。由图可知，油膜厚度在单坑位置明显增大，接触区其他位置与光滑表面相比略有减小；油膜压力在接近单坑位置时先减小后急剧增大，且第1次压力峰值比光滑表面的大一半左右，第2次压力峰值二者相差不大。

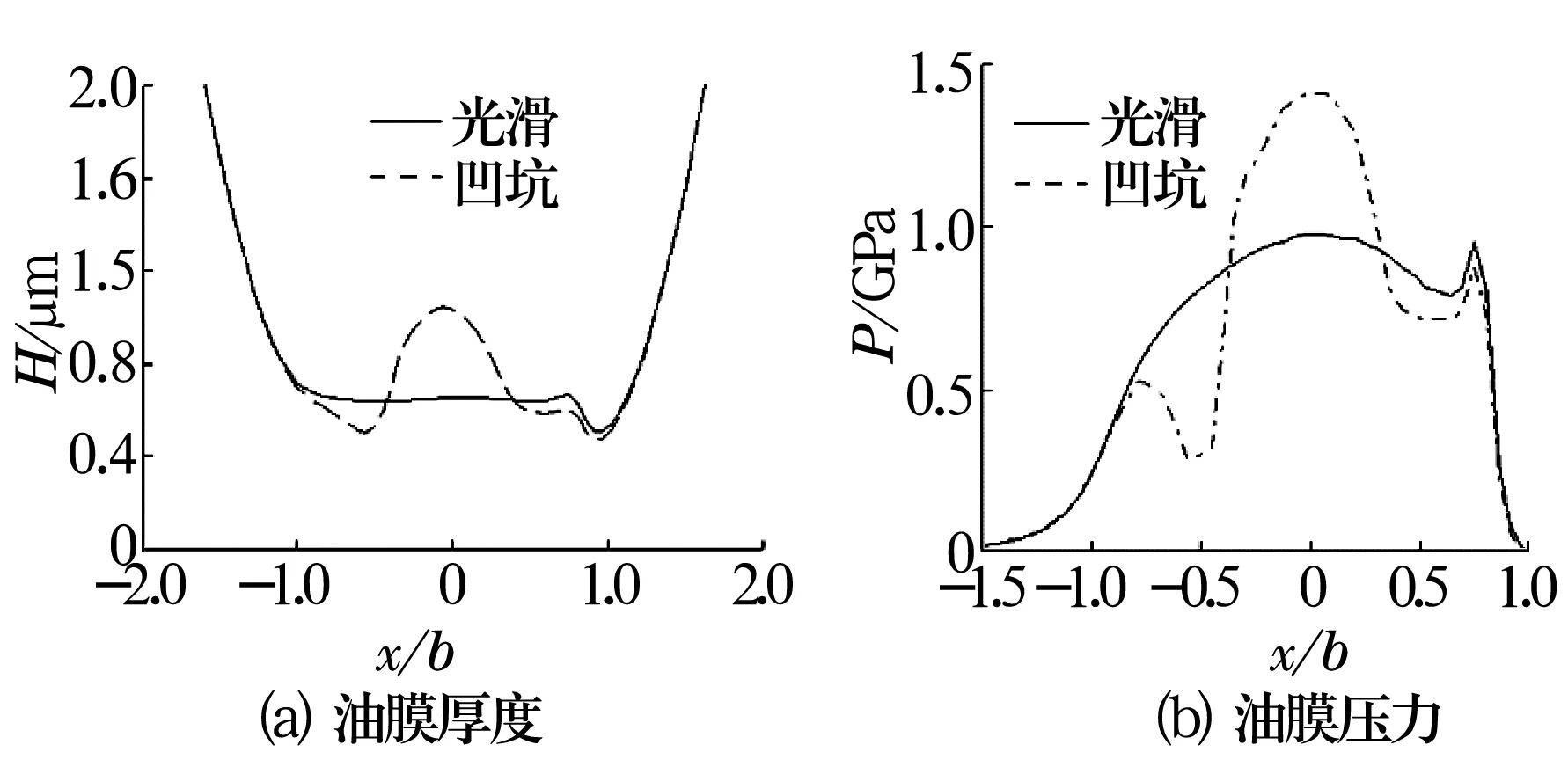
图4 y=0截面上油膜厚度和油膜压力

4.1.2 固定形貌时坑深对滚子热弹流润滑的影响

当单坑的形貌固定(即凹坑弧度均取120°)时，随着坑深增大，坑的外径也随之变大，坑深不同时y=0截面上油膜厚度和油膜压力如图5所示。

由图5a可知，油膜厚度在单坑位置明显增大，坑深越大，油膜厚度增大越明显；由图5b可知，油膜压力先减小后增大，坑深越大，油膜压力变化的幅度也越大。由此可知，油膜厚度与油膜压力的变化均随坑深的增大而增大，坑深与二者之间均为正比关系。

图5 坑深不同时y=0截面上油膜厚度和油膜压力

4.1.3 变形貌时坑径对滚子热弹流润滑的影响

当坑深固定时，凹坑弧度越小，坑径越大，坑径不同时y=0截面上油膜厚度和油膜压力如图6所示。

由图6a可知，油膜厚度在单坑位置明显增大，凹坑的弧度越小，即坑径越大时，油膜厚度增大越明显，且凹坑处最大油膜厚度也向入口处偏移，这是由供油区域半径增大而使供油更加充分导致的；由图6b可知，油膜压力先减小后增大，弧度越小，即坑径越大，第1次压力峰越向入口处偏移，油膜压力变化的幅度也越大。

图6 坑径不同时y=0截面上油膜厚度和油膜压力

4.1.4 固定形貌时速度对滚子热弹流润滑的影响

速度U00对光滑及单个微坑表面的圆锥滚子热弹流润滑的影响分别如图7、图8所示。由图7可知，光滑表面时，速度对油膜压力影响不大，而随着速度的增大，油膜厚度明显变大；由图8可知，速度越大，油膜厚度越大，单坑接触区油膜厚度变化幅度更大，油膜压力也随之变大，且变化幅度随速度的增大而增大，第1次压力峰向中心接触区移动。即在光滑与单个微坑表面，速度对油膜厚度的影响是一致的；而存在单个微坑表面时，速度对油膜压力有一定影响，这与光滑表面不同。

图7 速度的影响(光滑)

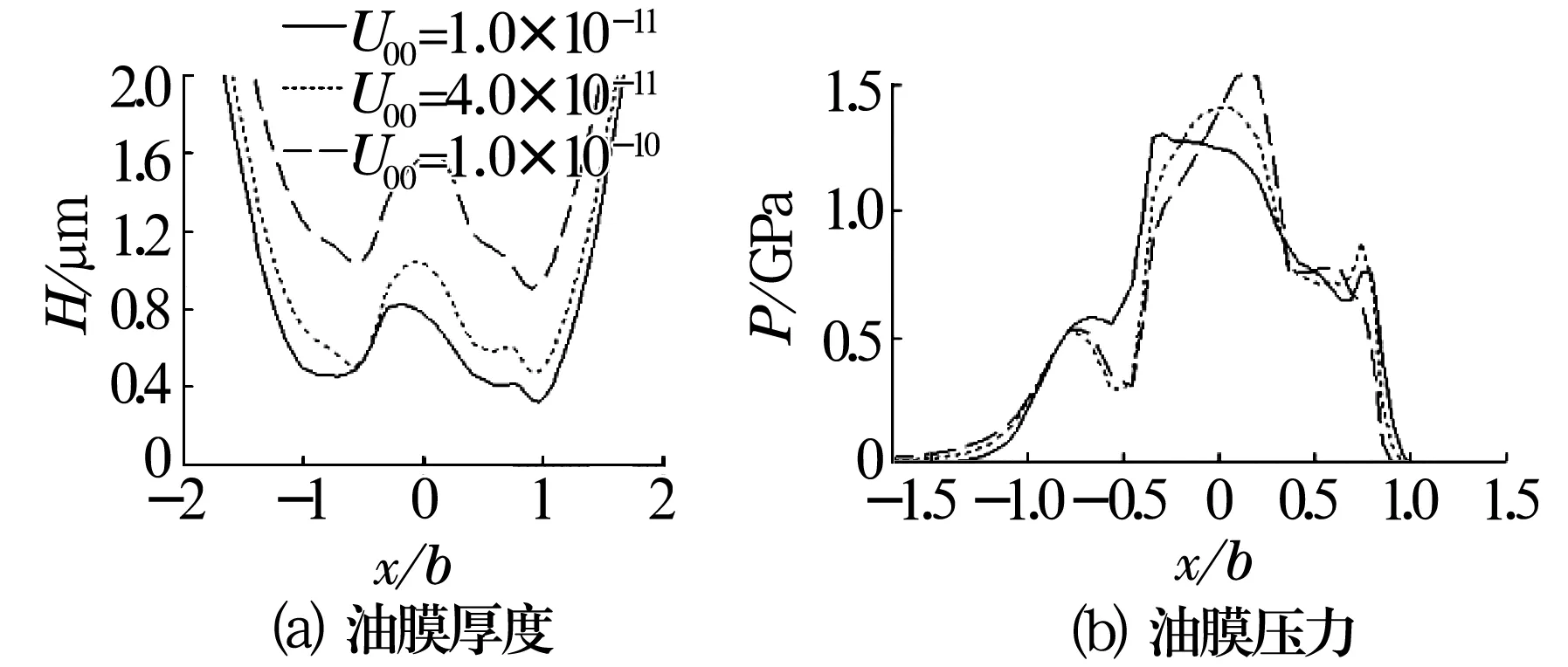
图8 速度的影响(凹坑)

4.1.5 固定形貌时载荷对滚子热弹流润滑的影响

最大Hertz应力(载荷)对光滑及单个微坑表面的圆锥滚子热弹流润滑的影响分别如图9、图10所示。由图9可知，光滑表面时，载荷对油膜厚度影响不大，而随着载荷越大，油膜压力有明显变大的趋势；由图10可知，随着载荷的增大，除了单坑接触区的油膜厚度变大外，其他接触区油膜厚度变化不大，而油膜压力随之增大。即在光滑与存在单个微坑表面，载荷对油膜厚度和压力的影响是基本一致的，但载荷越大，单坑区域油膜厚度和压力的变化越明显。

图9 载荷的影响(光滑)

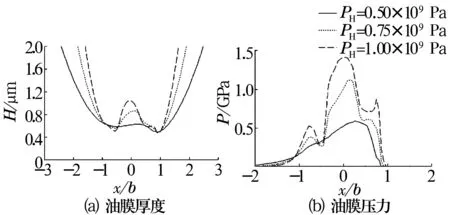
图10 载荷的影响(凹坑)

4.2 反向圆锥滚子模型参数分析

4.2.1 光滑及单个微坑表面时的热弹流润滑结果

根据弹流润滑结果对比了光滑表面与单个微坑表面时y=0截面上油膜厚度和油膜压力的变化，如图11所示。由图可知，油膜厚度在单坑位置明显增大，在接触区其他位置与光滑表面相比略有减小；油膜压力在接近单坑位置时先减小后急剧增大，第2次压力峰二者相差不大。

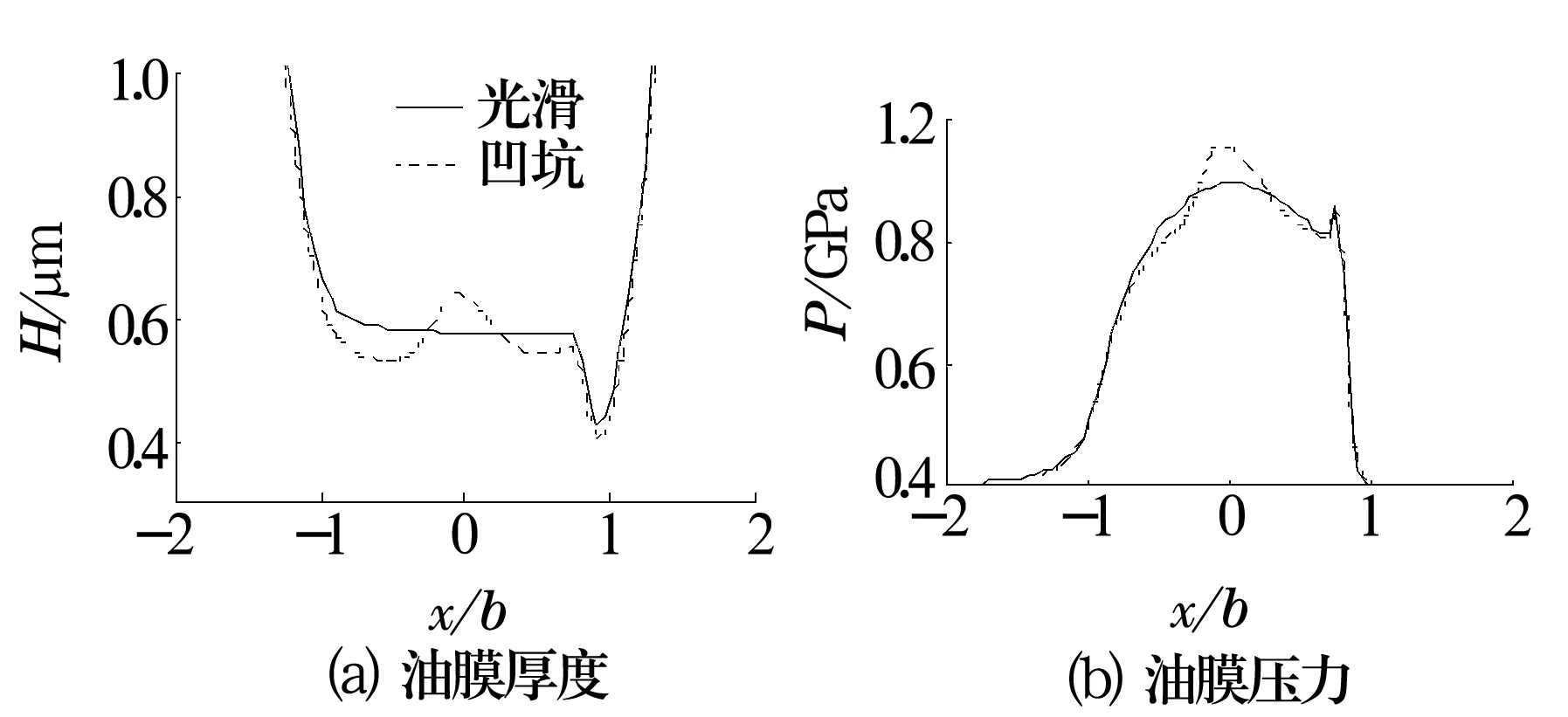
图11 y=0截面上油膜厚度和油膜压力

4.2.2 固定形貌时坑深对滚子热弹流润滑的影响

当单坑的形貌固定(即凹坑弧度均取120°)时，随着坑深增大，坑的外径也随之变大。坑深不同时y=0截面上油膜厚度和油膜压力如图12所示。由图12a可知，油膜厚度在单坑位置明显增大，随着坑深的增大，油膜厚度增大越明显；由图12b可知，油膜压力先减小后增大，坑深越大，油膜压力变化幅度也越大。由此可知，油膜厚度与油膜压力的变化均随坑深的增大而增大，坑深与二者之间均为正比关系。

图12 坑深不同时y=0截面上油膜厚度和油膜压力

4.2.3 变形貌时坑径对滚子热弹流润滑的影响

当单坑的深度固定时，凹坑弧度减小，则坑径增大。坑径不同时y=0截面上油膜厚度和油膜压力如图13所示。由图13a可知，油膜厚度在单坑位置明显增大，凹坑的弧度越小，即坑径越大时，油膜厚度增大越明显，且凹坑处最大油膜厚度也向入口处偏移，这是由供油区域半径增大而使供油更加充分导致的；由图13b中可知，油膜压力先减小后增大，弧度越小，即坑径越大时，第1次压力峰越向入口处偏移，油膜压力变化的幅度也越大。

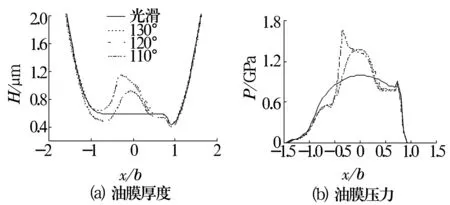
图13 坑径不同时y=0截面上油膜厚度和油膜压力

4.2.4 固定形貌时速度对滚子热弹流润滑的影响

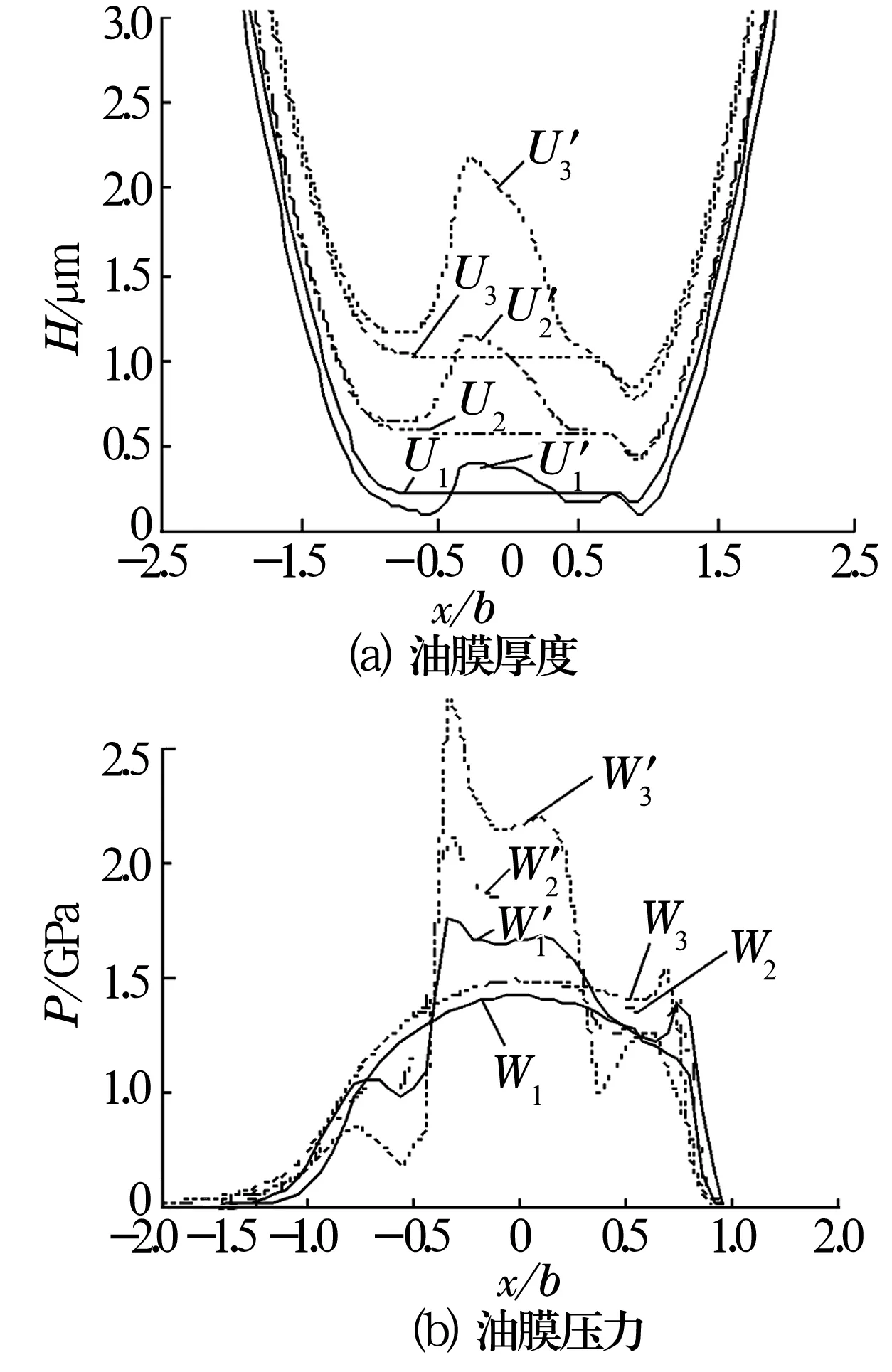
图14 速度对油膜厚度与油膜压力的影响

4.2.5 固定形貌时载荷对滚子热弹流润滑的影响

最大Hertz应力(载荷)对光滑及单个微坑表面的圆锥滚子热弹流润滑的影响如图15所示。对比可知，光滑表面时载荷越大，油膜压力越大，油膜厚度也越大；对于单个微坑表面，载荷越大，接触区油膜厚度越大，其他接触区油膜厚度变化不大，油膜压力也随之增大。即在光滑与存在单个微坑表面，载荷对油膜厚度和油膜压力的影响是基本一致的，但载荷的增大会使油膜压力及油膜厚度变化趋势更加明显。