编织纹路对自润滑关节轴承接触应力的影响

2014-07-21段闯创邱明康鹏飞陈龙李迎春

轴承 2014年10期

段闯创，邱明，康鹏飞，陈龙，李迎春

(1.河南科技大学机电工程学院，河南洛阳 471003；2.新昌县产品质量监督检验所，浙江新昌 312500)

1 前言

自润滑编织衬垫关节轴承使用一层编织材料作为润滑层，由于该材料强度大、柔性好、抗冲击、有自润滑功能，因此广泛应用于航空航天、铁路、矿山机械等领域[1]。关节轴承使用最多的是PTFE和芳纶纤维编织而成的自润滑衬垫。将其粘贴在轴承外圈内表面，与关节轴承内圈外表面形成配合面[2]。详细结构如图1所示。

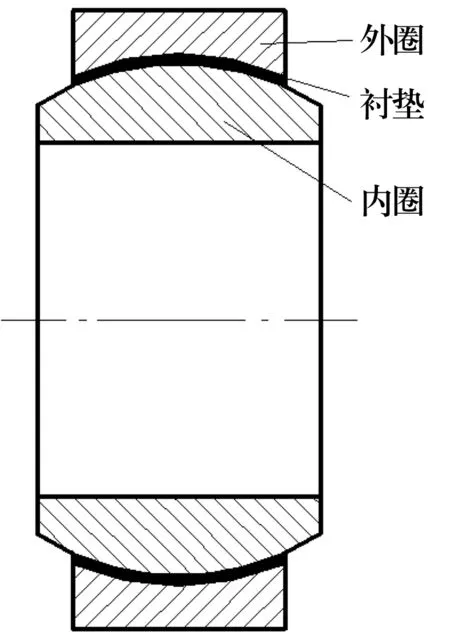
图1 编织衬垫关节轴承结构示意图

衬垫的编织方式有平织和斜织，其结构如图2所示。图2a中粘贴在轴承外圈上的衬垫与关节轴承径向平面所成夹角为45°，称作45°纹路编织衬垫；图2b中二者夹角为90°，称作90°纹路编织衬垫。

图2 编织衬垫示意图

对于纤维编织材料，国内外学者进行了相关研究，但只是通过衬垫的微观结构得到整体编织材料的物理性能[3-5]。而且由于编织衬垫的结构复杂，常规手段无法测得其接触部位的应力状态。随着计算机的发展，运用有限元仿真分析解决实际工程问题已经很普遍。下文采用有限元方法模拟编织衬垫在关节轴承上的应用，进一步探讨接触应力、变形与衬垫编织纹路的关系。

2 问题简化和建模

由于编织衬垫关节轴承整体结构尺寸简单，考虑到计算精度和计算时间，对其整体建模进行分析。

内、外圈和衬垫都采用三维可变形实体进行建模，轴承为内径20 mm的自润滑编织衬垫关节轴承。各部件的材料参数[5]见表1。表中，E，G，ν分别为材料的弹性模量、剪切模量和泊松比；下标1，2，3分别代表x，y，z方向。

表1 模型各部分的材料参数

内、外圈采用GCr15轴承钢，为各向同性材料，其弹性模量和泊松比为常数，又由于其形状规则，故忽略倒角和外圈裂纹。而编织衬垫为各向异性体，其材料参数在各个方向不同。

在ABAQUS材料定义模块中定义衬垫的等效材料参数(表1)，运用复合材料层合板的材料特性模拟衬垫的编织纹路，即在衬垫三维实体中建立两层等厚度的铺层，其纤维束方向可以自定义，夹角就是模拟的编织纹路的夹角。图3a和图3b分别为45°纹路衬垫和90°纹路衬垫的ABAQUS层合板模拟示意图。采用建立参考点的方法确定边界条件，分别把内圈内表面和外圈外表面约束到新建立的参考点1和参考点2上，参考点1为全约束，参考点2沿x方向施加23.863 kN的应力并约束其旋转自由度，得到的整体模型如图4所示。

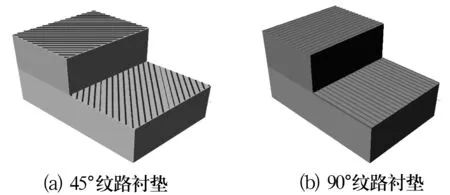
图3 ABAQUS层合板模拟示意图

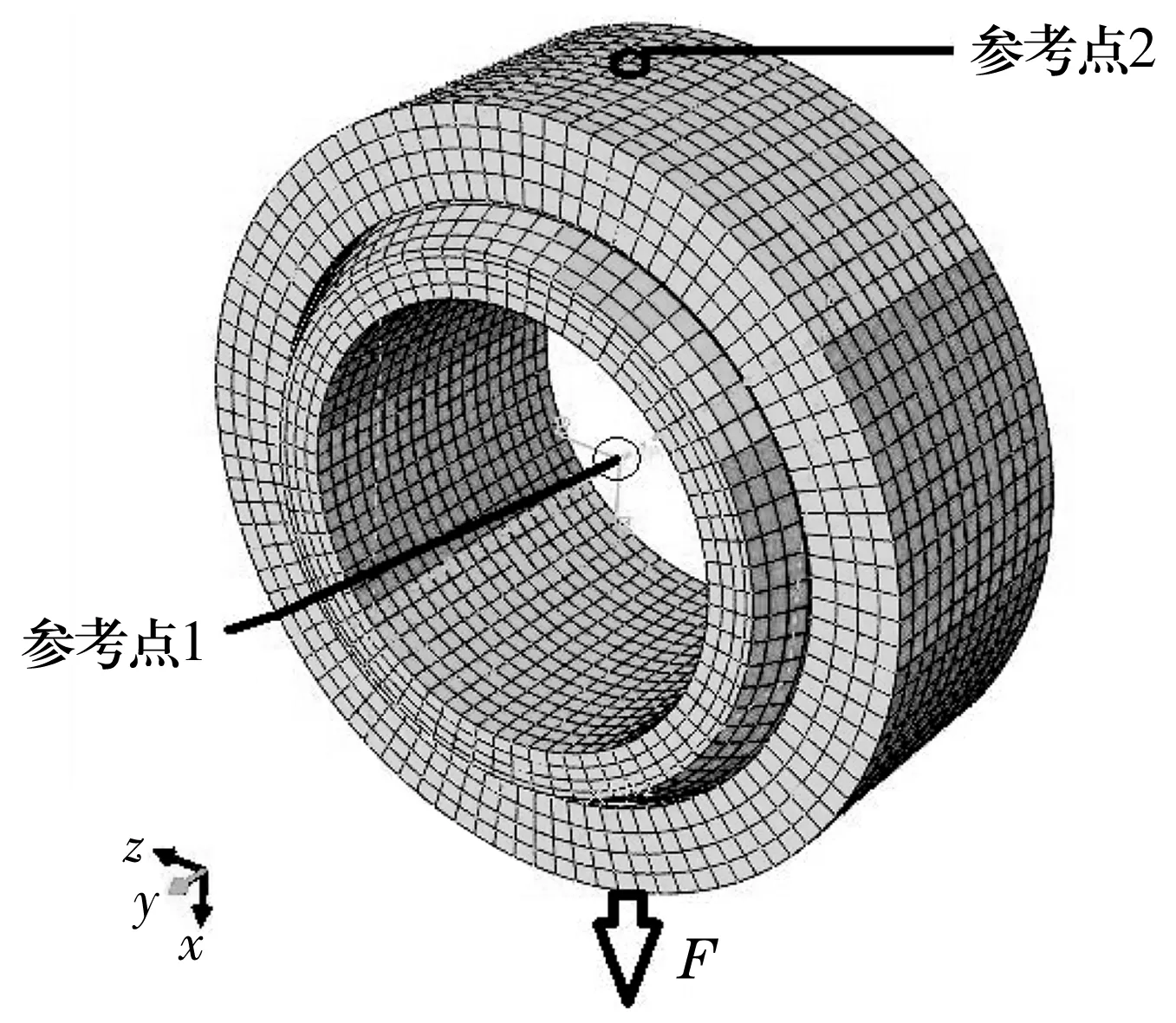
图4 整体模型图

3 结果分析

通过有限元软件ABAQUS进行分析，得到衬垫和内圈接触面的接触应力分布和衬垫接触面上的节点位移云图(图5)。

从图5a和图5b中可以看出，衬垫最大接触应力在接触部位最上方的两端面， 45°纹路衬垫最大接触应力为207.9 MPa，90°纹路衬垫的最大接触应力为218.7 MPa。从图5c和图5d中可以看出，衬垫和外圈沿x方向挤压内圈，由于内圈沿受力方向固定，衬垫接触部位受到内圈的阻碍，故沿受力方向的位移比未接触部位的小。

图5 衬垫与内圈接触面间的接触应力及衬垫位移分布

不同路径上节点的接触应力和位移如图6所示。路径1是衬垫接触面与径向平面的交线，按弧度进行划分，顶点对应0，整个路径从-π～π。路径2是衬垫接触面与轴向平面的交线，也按弧度划分，顶点对应的为0，整个路径是一段圆弧。

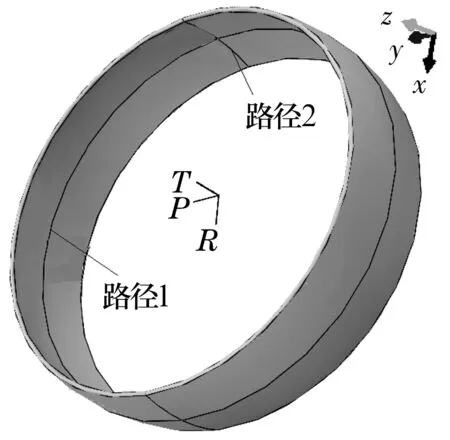
图6 衬垫路径示意图

接触面上的节点沿路径1的接触应力和沿载荷方向(x方向)位移分布如图7所示。由图可知，沿着路径1方向，衬垫接触应力与x方向上的位移量成反比关系，这是由接触部位内圈的阻碍作用引起的。两种纹路编织衬垫接触应力沿路径1方向分布基本一致，x方向上的位移分布在接触部位相差不大，但在非接触部位，45°纹路衬垫的位移分布高于90°纹路衬垫。由此可以推断在相同的载荷下，45°纹路衬垫的变形量略大于90°纹路衬垫。

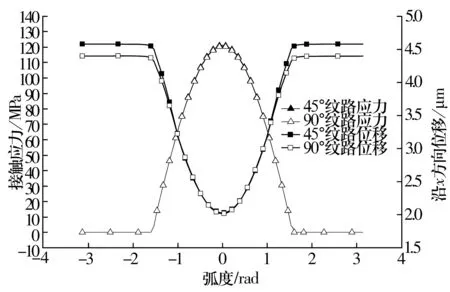
图7 衬垫接触应力和x方向上的位移(路径1)

衬垫接触面上的节点沿路径2方向接触应力和x方向上的位移分布如图8所示。由图可知，最大接触应力出现在路径开始和结尾(衬垫两端面)处，90°纹路衬垫的应力集中现象比45°纹路衬垫的明显，且位移比45°的小。因此可以得出45°纹路衬垫整体刚度略低于90°纹路衬垫，可很好地缓解应力集中现象，使接触应力分布更均匀，使轴承寿命更长。