基于ANSYS对某含有凹坑缺陷发酵罐的静力分析

2019-02-04时黛林国庆

当代化工 2019年11期

时黛林国庆

摘要：对含有凹坑缺陷的发酵罐按照GB/T19624-2004《在用缺陷压力容器安全评定》进行安全性评定，在此基础上利用ANSYS对不同间距的轴向排列的多凹坑进行静力分析，得到轴向排列的多凹坑的最大应力值和应力集中系数与相邻凹坑间距和数量的关系。经过分析可知，当相邻凹坑间距增大到L/X≥3.0时，各凹坑之间的应力分布几乎无影响;应力集中系数随着两凹坑中心距的增加而减小，当间距L/X<3时其变化幅度较大，当L/X≥3后趋于恒定;同时最大应力值和应力集中系数与凹坑缺陷数量成正比，而与相邻的凹坑间距成反比。

关键词：凹坑;安全评定;静力分析;应力集中系数

中图分类号：TQ 051.3 文献标识码： A 文章编号： 1671-0460（2019）11-2564-05

Static Analysis of Fermentation Tank With Pit Defect Based on ANSYS

SHI Dai， LIN Guo-qing^*

（College of Mechanical and Electrical Engineering， Jilin Institute of Chemical Technology， Jilin Province Jilin City 132022， China）

Abstract： Safety assessment of fermentation tank with pit defect was carried out in accordance with GB/T19624-2004 "Safety Assessment of Pressure Vessels with Defects in Use". On this basis， the static analysis of multi-pits with different spacing was carried out by ANSYS， and the maximum stress value and stress concentration coefficient of multi-pits with axial arrangement and between adjacent pits were obtained. The relationship between distance and quantity showed that when the distance between adjacent pits increased to L/X≥3.0 the stress distribution between the pits had little effect. The stress concentration factor decreased with the increase of the distance between the two pits， the variation range was larger when the distance L/X<3 and tended to be constant while the distance L/X>3. At the same time， the maximum stress value and the concentration factor were proportional to the number of pit defects and inversely proportional to the distance between adjacent pits.

Key words： Pits; Safety assessment; Static analysis; Concentration factor

在腐蝕环境下而形成的腐蚀凹坑是引起金属材料发生失效的主要形式之一，腐蚀凹坑形成后会导致裂纹的萌生及扩展，最终发生失效而缩短部件的使用寿命，通常虽然腐蚀速率较慢，但一旦腐蚀凹坑形成其点蚀速度却非常快，严重威胁着设备的安全运行。

本文中发酵罐主要应用在沼气工业中，其发酵物料主要为生活垃圾等带有腐蚀性的介质，所以随着发酵罐的运行和服役时间的推移，势必会在罐体上产生腐蚀等，很容易在罐体的内表面形成大量的腐蚀凹坑。因凹坑缺陷破坏了结构的连续性，会使缺陷部位发生应力集中现象^[1]，同时由于发酵罐在运行时其内部物料的一些物化特性变化而使发酵罐处于复杂的工作环境中，加大了凹坑处产生裂纹及扩展的可能性，使发酵罐的承载能力及安全性受到严重挑战。因此，有必要对含有不同结构尺寸及数量的凹坑进行静力分析并进行安全评定。

1 凹坑尺寸的确定

发酵罐内表面的凹坑多数是因腐蚀而引起的，其表面粗糙不光滑，易引起应力集中，使安全性降低，因此在进行安全评定及应力分析前，首先应把凹坑尽量打磨光滑，使表面无明显的腐蚀迹象^[2]，同时也要保证腐蚀凹坑从坑底到罐体内表面要过渡平缓，且不可出现急剧变化的截面，凹坑的数量以及相邻凹坑的间距都影响着发酵罐的使用寿命，对于同一条件下凹坑所引起的应力，其轴向排列的凹坑所产生的应力要明显高于环向排列的凹坑应力^[3]，故本文主要针对轴向排列的凹坑进行研究。

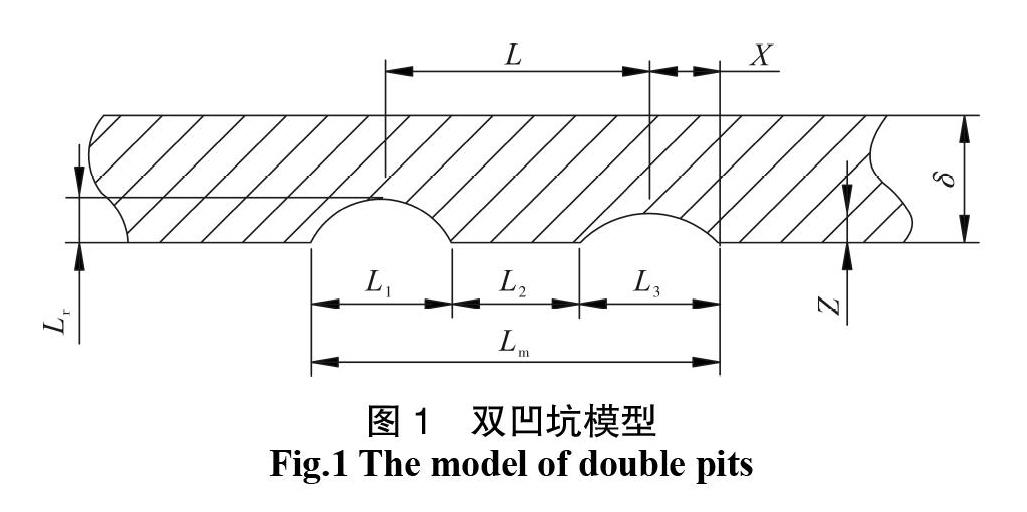
发酵罐选择含有浅球凹坑的圆柱形壳体为研究对象，其设计压力为0.3 MPa，设计温度为100 ℃，盛装生活垃圾等半固体物料，罐体所用材料为Q345R，筒体内径为1 000 mm，焊接接头系数为1，弹性模量209 GPa，泊松比0.28。双凹坑的尺寸示意图如图1所示。

通常，腐蚀凹坑多位于罐体的内表面，凹坑深度<10% 时，其影响可忽略，但当凹坑深度达到（10%～80%）时，需要对压力容器重点监测^[4]。假设凹坑的x方向的宽度一致均取2X=50 mm，分析两凹坑的圆心距与X方向宽度为不同比值时的应力分布情况，即L/X分别取0、1、2、3、4和5。为了使研究具有代表性，选择凹坑深度为4 mm。

2 凹坑缺陷的安全评定

腐蚀缺陷的存在会使发酵罐的强度降低，对发酵罐的安全运行产生隐患。因此，需要对含有凹坑缺陷的发酵罐进行安全评定，以确保其安全性。

对含有凹坑缺陷的发酵罐进行安全评定的步骤为^[5]：

（1）识别缺陷;

（2）确定缺陷部位及尺寸;

（3）确定材料性能数据;

（4）计算无量纲参数G₀及判别免于评定的情况^[6];

（5）确定塑性极限载荷P_L及最高容许工作压力P_max;

（6）安全性评定。

2.1 計算G₀和判别免于评定的情况

罐体表面凹坑缺陷的无量纲参数G₀可按下式计算：

（1）

若G₀≤0.1则认为该凹坑缺陷是安全的或可以接受的，可免于评定;否则应进行评定。

根据公式（1）可以算出所选单凹坑的G₀值，

由上述计算可知所选凹坑G₀>0.1，按照GB/T 19624-2004中的要求须对其进行安全评定。

2.2 对G₀>0.1的凹坑进行安全评定

为了研究这些蚀坑对罐体的使用寿命的影响，对于无凹坑缺陷的圆柱形容器壳体的塑性极限载荷 P_L0的计算可按下式进行^[7]：

其中： —材料流动应力，取法如下：

非焊缝区凹坑，;

焊缝区凹坑，。

其中焊接接头系数f可按实际设计条件选取，也可以根据GB150-2011或者其他标准选取。

对含有凹坑缺陷圆筒形容器的极限载荷P_L可按下式计算得到^[8]：

而最高容许工作压力P_max的计算为：

由于P<P_max，因此单凹坑时罐体安全。

按照GB/T19624-2004《在用缺陷压力容器安全评定》在进行评定前需要判别两个相邻凹坑之间是否会产生干涉，若各凹坑之间的距离满足L₂<L_l+L₃则认为两凹坑轴向发生相互干涉，此时将多凹坑视为同一等效凹坑^[9，10]，等效凹坑的轴向尺寸为L_m=L_l+L₂+L₃，周向尺寸为L_r。因此在多凹坑中，当相邻两凹坑间距为L/X≤3时，满足将多凹坑视为同一凹坑的条件，因此按照上述计算方法同理可求得各间距下的最高容许工作压力P_max。其他间距的凹坑在进行安全评定时因其可视为单凹坑故计算结果与单凹坑计算结果相同，最终计算结果如表1所示。

从表1中可以看出，虽然存在这些凹坑缺陷，但罐体的设计压力始终小于最高容许工作压力，即P<P_max，因此罐体仍处于安全状态。

3 凹坑有限元分析

3.1 凹坑有限元计算模型

由于所取壳体与整个壳体相比较小，可以认为在几何尺寸及载荷上具有对称性^[11]，在用有限元建模时只需建立壳体的二分之一即可模拟出整个罐体的情况，设置好单元类型及材料属性后，按照上述凹坑尺寸建立轴向排列的多凹坑有限元模型，划分单元并在纵向对称面施加对称约束^[12]，其有限元模型如圖2所示。

3.2 轴向排列双凹坑有限元结果分析

考虑凹坑在发酵罐中往往并不是单独存在的，同时凹坑排列也是无章可循的，为了便于分析将凹坑的分布理想化处理，将其分为轴向排列和环向排列，其对发酵罐的使用寿命等由不同的影响。同时，凹坑数量及间距等因素对发酵罐的应力分布影响也不同，轴向排列的凹坑要比环向排列的凹坑危害性要大，因此本文将重点研究发酵罐的轴向排列的凹坑的应力分布情况以及对发酵罐安全性的影响（图3）。

从图3中可以看出，当L/X=1即单凹坑时，其最大应力为32.727 5 MPa，所在位置为凹坑的底部，至凹坑边缘逐渐减少，凹坑周围除在凹坑的环向方向出现对称的局部应力减小情况外，其余地方应力几乎相同，没有太大的波动。

当L/X=1即两凹坑相交时，凹坑最大应力为37.278 9 MPa，位于凹坑底部，随着相邻凹坑间距的增加，其最大应力呈逐渐减少的趋势，至L/X=5时，其最大应力值为29.838 6 MPa，随着蚀坑间距的变化至L/X≥3时，相邻凹坑间的最大应力将在各自凹坑的底部，且其值与单凹坑的最大应力值相差不大。另外需要注意的是当L/X≤2即相邻两凹坑相切及相交时，其在进行应力分析时由于其中心距的原因可将其视为同一凹坑来处理，同时，随着凹坑间距的增加，凹坑周围的应力数值及影响区域也逐渐扩大，主要是因为两凹坑相切及相交时其截面形状发生突变导致其应力出现较大幅度增加，但随着凹坑间距的增加，即间距在L/X≥3时，相邻两凹坑对应力的影响并不大，基本可以忽略。

3.3 轴向排列三凹坑有限元结果分析

从图4中可以看出，当L/X=0即单凹坑时，最大应力为32.727 5 MPa，其值低于L/X=1、L/X=2时三凹坑的最大应力，说明在恒压作用下，当多凹坑距离较近时所产生的应力要大于单凹坑的应力，这也意味着多凹坑时要比单凹坑危险。

当L/X≤3时，相邻凹坑之间会发生干涉^[13]，因此在做研究时应将其视为一个凹坑。当两凹坑相距较远（L/X>3）时，凹坑的最大应力值与单个凹坑的最大应力差异较小，这也符合GB/T19624-2004中的规定。

3.4 应力集中系数的计算

由于凹坑缺陷的存在，在凹坑处势必会产生应力集中现象，应力集中系数作为衡量应力集中程度的主要参数，在实际分析研究中具有重要意义^[14]。根据应力集中系数的定义知：

（2）

式中：k_t—应力集中系数;

σ_max —最大正应力，MPa;

σ_n —名义正应力，MPa。

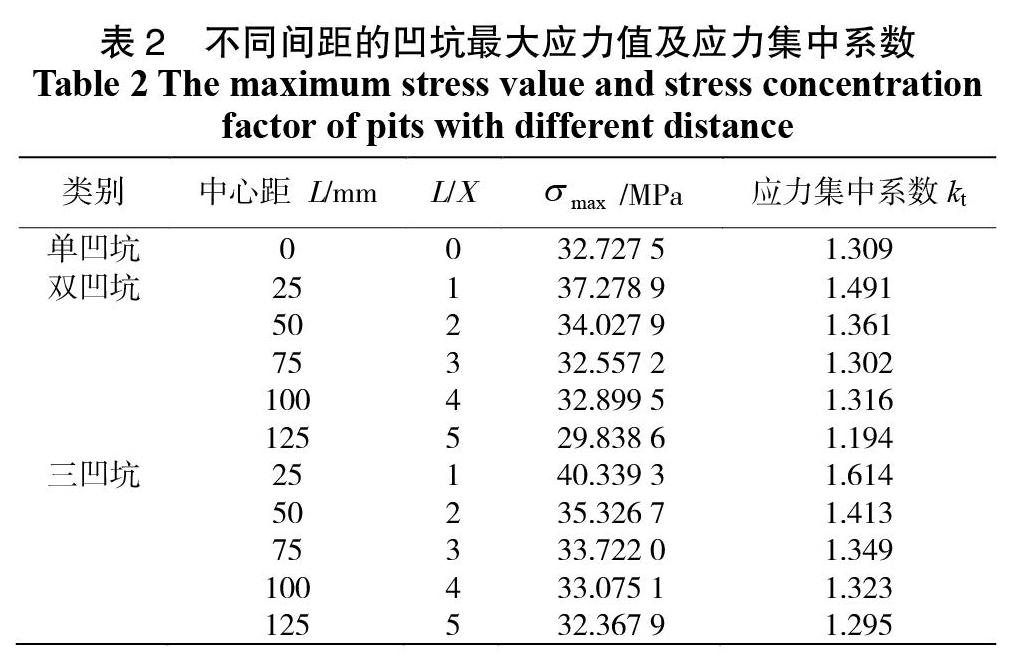
对于受恒压的发酵罐体而言，其名义正应力为，为没有缺陷时所对应的最大环向应力。从而可计算出应力集中系数，计算结果汇总如表2所示。

从表2可得出，当凹坑之间的中心距在L/X=1时其应力达到最大值，之后随着相邻凹坑中心距的增加其应力和应力集中系数也随之降低，当中心距达到一定程度（L/X≥3.0）时，轴向排列的多凹坑，无论是双凹坑还是三凹坑，其最大应力和应力集中系数受相邻两凹坑之间的距离影响并不明显。此外，从图5中可以看出，单凹坑的最大应力值和应力集中系数与双凹坑和三凹坑相比最小，即最大应力值和应力集中系数与凹坑数量成正比。

无论相邻凹坑距离多少，三凹坑的应力集中系数始终大于同一距离条件下的应力集中系数^[15]，说明凹坑缺陷的数量对发酵罐的应力分布及寿命有很大影响。

4 结论

（1）凹坑缺陷的存在会导致局部应力集中现象，产生峰值应力，使发酵罐的安全运行受到威胁。通过对含有凹坑缺陷的罐体进行安全性评定可知，虽然罐体存在这些凹坑缺陷，但设计压力始终小于最高容许压力，即罐体处于安全状态;但需注意的是罐体若长期在交变载荷的作用下，容易造成罐体疲劳破坏，应引起足够重视。

（2）轴向排列的凹坑，如果相邻凹坑的间距达到某一数值（L/X≥3.0）时，对应力分布的影响并不大;同时，应力集中系数随着两凹坑中心距的增加而减小，当间距L/X<3时其变化幅度较大，而L/X≥3后趋于恒定。

（3）最大应力值和应力集中系数与凹坑缺陷的数量成正比，而与相邻的凹坑间距成反比，即凹坑数量越多其最大应力和应力集中系数越大，而随着相邻两凹坑的间距增加，其最大应力值和应力集中系数降低。

参考文献：

[1]纪晓懿，金长义.含凹坑缺陷的薄壁圆筒形压力容器疲劳寿命数值模拟研究[J].化工技术与开发，2008，37（7）：42-45.

[2]张翼.边缘应力区局部减薄强度特征的研究[D].天津大学，2006.

[3]赵菊.压力容器蚀坑群干涉效应及安全评价[D].辽宁石油化工大学，2010.

[4]帅健，于桂杰.管道及储罐强度设计[M].北京：石油工业出版社，2006.

[5]任国栋，周吉军.在用含凹坑缺陷的压力容器合于使用评价[J].化学工程与装备，2016，（7）：148-149.

[6]徐尊平，雷斌隆.含弧坑缺陷壓力钢管的安全评定[J]电焊机，2006，36（8）：53-54.