基于多元回归法的酸洗线和镀锌线用轴承维修策略
2014-07-21王桂梅李艳强李永利宋辉
王桂梅,李艳强,李永利,宋辉
(1.河北工程大学 机电学院,河北 邯郸 056038; 2.务腾咨询(上海)有限公司 北京分公司,北京 100025; 3.河北钢铁集团,河北 邯郸 056038)
随着科学技术的发展,钢铁生产设备逐渐向机电液一体化方向发展,设备的性能不断得到改进和提高,对设备的维修、可靠性与更换的经济性也提出了非常高的要求。事后维修和定期维修的主要缺点是过维修和欠维修,导致设备“带病工作”和“无病诊断”,已不能满足现代化生产方式的需求,取而代之的是视情维修。
某钢厂的酸洗线与镀锌线使用大量轴承,在高速复杂的系统中经常出现损坏,以往根据维修人员的触觉感触轴承温度,超过70 ℃时进行更换,实时性和准确性较差。在此,运用多元回归法对轴承温度进行预测,进而采取相应的维修策略,防止因突发性损坏及人为疏忽导致生产线停工造成的巨额损失。
1 视情维修
视情维修又称状态检测维修(Condition Based Maintenance,CBM),是随着检测和诊断技术快速发展而形成的一种新的维修策略,视情维修强调对系统或设备进行状态检测和诊断,并评估系统劣化状况,从而根据分析和诊断结果安排维修时间和维修项目。
视情维修根据机内或外置检测设备所获得的实际状态信息决定维修时间和方式。与传统的预防性定时维修的区别在于:视情维修制定维修策略时考虑了系统运行的状态及每个系统个体之间由于制造过程、使用保障过程等原因造成的差异,尽可能使每个系统在故障发生前的时刻进行维修,降低故障发生的概率,减少维修过程中的资源浪费。实施视情维修可以显著降低运行和维修费用,提高设备使用可靠度,改善工作过程,优化维修任务,减少故障发生次数并提高设备的利用率。
2 多元回归分析模型
回归分析法是分析相关因素相互关系的一种数理统计方法,通过建立1个或1组自变量和相关随机变量的回归分析模型预测相关随机变量的未来值。
多元线性回归分析是研究1个随机变量(因变量)y与2个及2个以上的一般变量(自变量)x1,x2,…,xm之间相互关系的统计分析方法。一般形式的多元线性回归分析模型为
y=b0+b1x1+b2x2+…+bmxm+e,
(1)
式中:b0为常项,又称为截距;b1,b2,…,bm为偏回归系数;e为残差。
如果有n组统计数据(yi;xi1,xi2,…,xim),i=1,2,…,n,则多元线性回归模型的矩阵形式为
Y=XB+V,
(2)
其中,Y=[x1,x2,…,xn]T,
B=[b0,b1,…,bn]T,
V=[e1,e2,…,en]T。
对于偏回归系数的估计值,可以由一元线性回归法求得。应用最小二乘法对b0,b1,…,bm进行估计,设Q为误差平方和,则
(3)
对Q求偏导数并令其等于0,整理得正规方程组
(4)
用矩阵形式表示为
B=(X′X)-1(X′Y),
所以多元回归法预测模型为
(5)
3 轴承温度预测
酸洗线在钢铁冶金领域的冷轧生产前起着关键作用,主要作用是借助于机械和化学作用去掉带钢钢卷表面氧化铁皮及污垢,得到表面清洁的带钢。镀锌线的主要作用是防止带钢被氧化和腐蚀。这2条生产线使用大量的调心滚子轴承,生产过程中经常出现轴承损坏。
根据现场的实际情况分析得出轴承(型号为22222CC/W33和23024CC/W33/C3)温度主要受振动和转速的影响,需现场采集振动、转速和温度3种数据。因轴承振动频率不太高,振动速度传感器(SZ-S)即可满足灵敏度需求,将其水平安装在轴承承载区域,底部用螺钉固定;转速采用接触式转速表(DT2235)测量,测量时转速表探头接触旋转轴;温度采用UT300非接触式红外测温仪测量,测量时将测温仪瞄准轴承,扣住扳机即可实时显示测量结果,松开扳机则保持读数。每天对振动、转速、温度3种数据进行8次采集(采集时刻为9~12和14~17时)。数据采集完成后进行数据处理,得到试验所需数据。
预计某钢厂的轴承寿命y受转速x1、振动x2影响,设y=b0+b1x1+b2x2。记录的原始数据见表1。
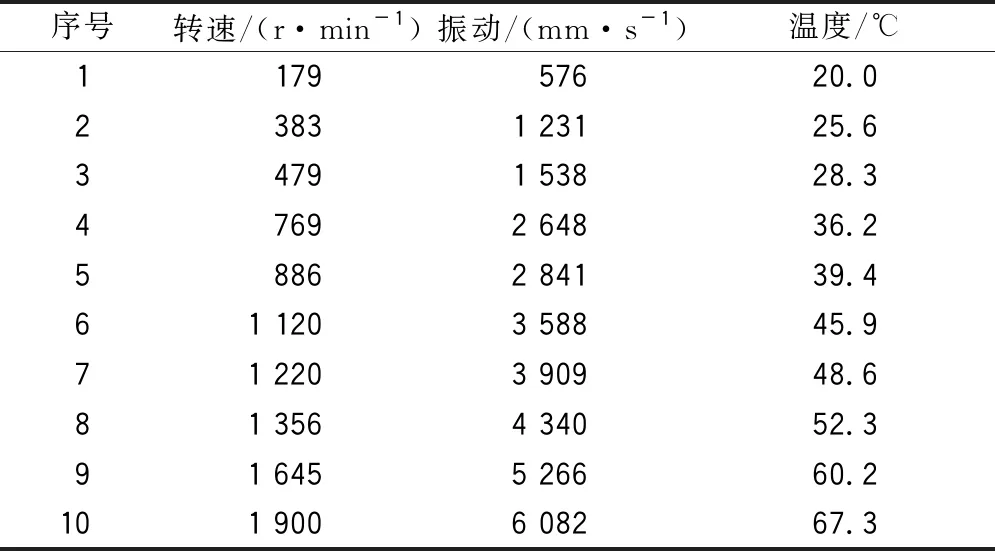
表1 试验原始数据(部分)
将试验数据代入正规方程组得
由此可求得,偏回归系数b0,b1,b2分别为15.077 0,0.006 8,0.006 5,所以y对x1,x2的回归方程为y=15.077 0+0.006 8x1+0.006 5x2,对此模型进行显著性检验得F>F0.05(2,92),表明回归方程为高显著。
根据回归方程及采集的数据对轴承温度进行回归预测,结果见表2。由表2可得,回归预测结果与实测数据基本相符,误差范围为0.087 0 ~0.396 4,满足设备实际维修需求,可以根据本回归模型对轴承温度进行预测,在预测温度高于70 ℃时更换轴承。
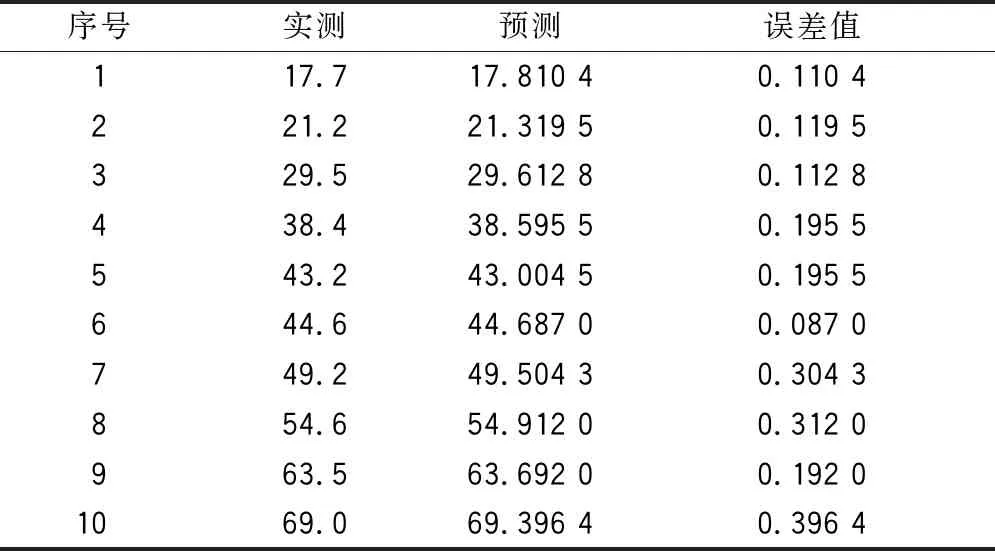
表2 轴承实测温度与预测温度对比 ℃
4 结束语
多元回归分析法计算简单、易于掌握,能够对采集的数据进行合理筛选和去伪存真,可以有效提高模型的预测精度。
借助多元回归分析法建立的数学模型,可较为准确地预测轴承温度,进而减少因轴承温度偏高而产生的维修费用,有效降低维修成本和设备故障率,提高企业的竞争力。需要强调的是,由于设备运行环境的复杂性,该模型不是一成不变的,应适时、定期地对其进行修正和补充。
