滚子凸度偏移和外滚道锥度对圆柱滚子轴承接触应力的影响

2014-07-21祝世超扈文庄夏新涛李军姜宗成

轴承 2014年10期

关键词：凸度锥度偏移量

祝世超, 扈文庄, 夏新涛, 李军, 姜宗成

(1.南方轴承股份有限公司,江苏常州 213000；2.洛阳轴研科技股份有限公司,河南洛阳 471039；3.河南科技大学机电工程学院,河南洛阳 471003 )

1 存在的问题

圆柱滚子轴承中，对数素线的圆柱滚子在加工制造时会产生一定的凸度偏移；外滚道在加工制造时会产生一定的锥度。这两者会对轴承的最大接触应力和接触应力分布产生重要影响，从而严重影响轴承的工作性能和寿命。

圆柱滚子素线的对数曲线如图1所示。滚子轴向和径向分别为x，y轴方向；对数曲线关于y轴对称，对称点和坐标原点O重合。凸度偏移是指对数曲线上的对称点相对坐标原点O产生一定的偏移 (偏移量为s)，如图2所示。

图1 圆柱滚子素线的对数曲线

图2 圆柱滚子的凸度偏移

外滚道锥度是指外滚道实际加工中不是一个理想的圆柱面，存在一个锥度β，如图3所示。

图3 外滚道锥度

在现有的研究中，只有关于对数素线滚子凸度大小对轴承接触应力影响的报道[1-3]，很少有外滚道锥度和滚子凸度偏移同时对轴承接触应力影响的研究。因此，文中以N1015圆柱滚子轴承为研究对象，采用ANSYS分析软件建立轴承的有限元分析模型，对滚子凸度偏移和外滚道锥度对轴承接触应力的影响进行静力学分析，以确定合理的凸度偏移量和外滚道锥度[4-9]。

2 有限元模型

2.1 轴承主要参数

轴承主要参数见表1。

表1 轴承主要参数

2.2 凸度设计

对数曲线滚子的素线方程为[6-9]

(1)

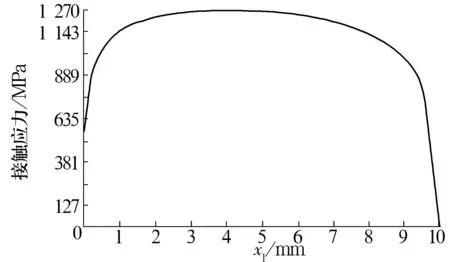
式中：x为对数曲线函数的自变量，-Lwe/2

滚子所受的最大载荷为

(2)

式中：Fr为径向载荷。

2.3 参数化建模

由于对数曲线在ANSYS中不能直接生成，所以采用参数化语言APDL命令流来建立圆柱滚子轴承有限元模型，N1015圆柱滚子轴承部分APDL命令流如下：

wpro,,,-90.0

Et,1,solid45

Mp,ex,1,208e3

Mp,prxy,1,0.3

*do,i,1,100

xpos=0.1*(i-1)

ypos=-0.00067701*(log(121-4*0.1*(i-1)*0.1*(i-1))/0.434294-4.79579)

k,i,xpos,ypos

*enddo

ksel,r,,,552,624

!cm,kcurve50,kp

bsplin,all。

2.4 网格划分

轴承扫掠网格划分的二分之一有限元模型如图4所示。模型的单元类型是solid 45。由于受计算机运算量的限制，为了减少网格数量并能精确求解，在滚子和内、外圈的有效接触部位进行了网格细分。轴向上滚子和内、外圈的网格尺寸约为0.07 mm，沿径向的网格尺寸约为0.006 mm。由于其他部位对计算结果影响不大，其网格可以适当稀疏。在接触部位，当有限元模型的网格边长尺寸小于接触半宽的50%时，计算结果已经足够精确。模型中滚子与内、外圈间的接触半宽为0.15 mm，所以该有限元模型的网格尺寸划分是合适的。

图4 N1015圆柱滚子轴承有限元模型

2.5 接触对的建立

由于研究对象是装配体，所以当有限元模型建好后，应通过建立接触对使不同的零件之间产生力或者位移传递。在创建接触对时，由于内、外圈面积较大，将其设为目标面，而圆柱滚子相对较小，将其表面设为接触面。在创建接触对时，接触刚度和穿透容差是2个需要设置的接触参数。经过多次试验，最终接触刚度系数设为1.5，穿透容差设为默认值，对于保证精度和收敛比较合适。

2.6 载荷施加

在施加边界条件时，先选择滚子的一个中间面，然后选择面上所有节点，再将其坐标系转为柱坐标系，约束滚子中间面上所有节点的y向位移，对滚子的剖面全部施加对称约束；选择外圈外表面上所有节点，在笛卡尔坐标系下约束所有自由度；在内圈内表面上先选择一个主节点，再选择一个从节点，对其进行径向自由度耦合，然后在主节点上施加载荷。

3 结果分析

经有限元分析，得到了径向载荷下滚子与内、外圈间的Mises应力及接触应力等分析结果。据此可以评估外滚道锥度和滚子凸度偏移对轴承接触应力的影响。

根据轴承的工况选择在0.2倍额定动载荷下对轴承进行有限元分析。首先分析凸度偏移量和外滚道锥度均为0时，滚子与外圈间的接触应力分布，结果如图5和图6所示。由图可知，滚子与外圈间的接触应力分布比较均匀且左右对称，最大值(1 235.6 MPa)出现在滚子中间部位xl=5.4 mm附近，并沿滚子轴向向两端缓慢降低。这种接触应力的分布有利于保证轴承的寿命和性能。研究还表明，滚子与外圈间的接触应力小于其与内圈间的接触应力，但是沿轴线方向的变化趋势相同。

图5 外滚道锥度和滚子凸度偏移量均为0时的接触应力分布

图6 外滚道锥度和滚子凸度偏移量均为0时的Mises 应力分布云图

外滚道锥度为0.005 729 58°，滚子凸度向左偏移0.1 mm时，滚子与外圈间的接触应力曲线和Mises 应力分布云图分别如图7和图8所示。由图可知，接触应力的最大值没有出现在滚子中部，而向左发生了偏移；滚子左端面(xl=0)附近与右端面(xl=10.6 mm)附近的接触应力分别为526.3 MPa和0，两端的接触应力差值较大，这表明接触应力的分布出现了异常，呈现出复杂的非对称性与非均匀性。

图7 外滚道锥度为0.005 729 58°和滚子凸度向左偏移0.1 mm时的接触应力分布

外滚道锥度为0.017 188 7°，滚子凸度向左偏移0.4 mm时，滚子与外滚道间的接触应力曲线和Mises 应力分布云图分别如图9和图10所示。由图可知，接触应力的最大值严重偏离滚子中部；滚子左端面(xl=0)附近与右端面(xl=10 mm)附近的接触应力分别为680.5 MPa和0，二者差值更大。由此表明，接触应力的分布严重异常，呈现出更为复杂的非对称性与非均匀性。

图9 外滚道锥度为0.017 188 7°和滚子凸度向左偏移0.4 mm时的接触应力分布

图10 外滚道锥度为0.017 188 7°和滚子凸度向左偏移0.4 mm时的Mises 应力分布云图

最大接触应力随滚子凸度偏移量的变化曲线如图11所示。由图可知，外滚道锥度为0.017 188 7°时，随着滚子凸度偏移量的增大，外圈与滚子间的最大接触应力非线性增大。当滚子凸度偏移量大于0.2 mm后，最大接触应力将迅速增大。这说明当外滚道锥度为0.017 188 7°时，滚子凸度偏移量0.2 mm是一个转折点。