主成分回归对脑卒中发病与环境因素间关系的解析
2014-06-12费妮娜杨有龙
费妮娜,杨有龙
(1.西安理工大学高等技术学院,陕西西安 710048;2.西安电子科技大学数学与统计学院,陕西西安 710071)
主成分回归对脑卒中发病与环境因素间关系的解析
费妮娜1,2,杨有龙2
(1.西安理工大学高等技术学院,陕西西安 710048;2.西安电子科技大学数学与统计学院,陕西西安 710071)
脑卒中的诱发已经被证实与环境因素包括气温和湿度之间存在密切关系.对脑卒中的发病环境因素进行分析可以对脑卒中高危人群进行风险评估并及时采取干预措施,而平均气压、最高气压、最低气压、平均温度、最高温度、最低温度、平均相对湿度、最低相对湿度8个自变量之间的共线性使得用多元线性回归方法得到的回归方程的精度降低.运用主成分回归分析,对脑卒中发病人数与环境因素进行了深入解析,结合统计软件SPSS的分析结果,给出了计算主成分的正确表达式,并将主成分与发病人数进行多元线性回归,最终确定了脑卒中发病人数与8个环境因素间的数学模型.
脑卒中发病;环境因素;主成分分析;数学模型
0 引言
2012年全国大学生数学建模竞赛C题为脑卒中发病环境因素分析及干预.作为指导教师,一直关注此赛题的研究进展及结果,发现绝大多数参赛队使用了多元线性回归的方法,但有的忽视了气象因素间的严重共线性给回归方程带来的影响.从2012年至今,几乎没有学者对克服这些现象再进行深入研究.而环境因素之间的严重共线性使得多元线性回归模型中偏回归系数难以估计,偏回归系数的估计方差随着解释变量相关性的增大而增大,偏回归系数的置信区间增大和偏回归系数估计值的不稳定性增强,以及偏回归系数假设检验的结果不显著等,都给回归方程的确立带来了严重的不可靠性[1].为了消除多重共线性给回归模型带来的不良影响,提出了一些改进的回归方法,其中比较有效的一种方法是主成分回归方法[2].经过与其他方法比较,本文在已有文献的基础上,利用excel表格进行数据处理与成分计算,借助统计软件SPSS17.0分析结果,正确使用主成分回归方法对脑卒中与环境因素的关系进行了分析,得到较为可靠的数学模型.
1 主成分分析的基本原理和计算步骤
1.1 主成分分析的基本原理
Hotelling于1933年提出的主成分分析方法的核心思想就是通过降维,把多个指标转化为少数几个综合指标,尽量不改变指标体系对因变量的解释程度.此方法适用于变量之间存在较强相关性的数据,如果原始数据相关性较弱,运用主成分分析后不能起到很好的降维作用,即所得的各个主成分浓缩原始变量信息的能力差别不大.一般认为当原始数据大部分变量的相关系数都小于0.3时,运用主成分分析不能取得很好的效果.W.FMassy在1965年根据主成分分析的思想提出了主成分回归方法.如今主成分回归方法已经被广泛应用,成为回归分析中解决多重共线性比较有效的方法.
假设对某一事物的研究涉及p个指标,分别用X1,X2,…,Xp表示,这p个指标构成p维随机向量为X=(X1,X2,…,Xp)′.设随机向量X的均值为μ,协方差矩阵为Σ.
对向量X进行线性变换,可以得到新的综合变量,用Z表示,即就是,新的综合变量可以由原来的变量线性表示,即满足下式:

其中p个互不相关的新变量中可以找到l个新变量(l<p)能解释原始数据大部分方差所包含的信息,包含的信息量是原始数据包含信息量的绝大部分.其余p-l个新变量对方差影响很小.我们称这p个新变量为原始变量的主成分,每个新变量均为原始变量的线性组合.
设y=(y1,y2,…,yn),假设X设计矩阵已经中心化,记λ1≥λ2≥…≥λp为X′X的特征根,Φ=(φ1,φ2,…,φp)为对应的标准正交化特征向量[3].
1.2 主成分回归的计算步骤
1)把原始数据进行标准化,以消除结果受量纲的影响;
2)诊断自变量之间的多重共线性,检验是否可以用主成分回归进行分析;
3)对所有标准化后的自变量,确定主成分的个数和特征值.最大的特征值对应第一主成分,第二大特征值对应第二主成分,以此类推.主成分个数的确定取决于主成分对因变量的解释程度.如果前i个特征值之和与所有特征值之和的比达到一定程度比如85%时,就可以认为这些主成分能代替所有的自变量体系.同时剔除特征值对应的比较小的那些主成分;
4)计算特征向量;
5)计算主成分的值;
6)对因变量y与主成分进行普通最小二乘回归,再返回到原来的参数,即可得出消除多重共线性后的标准回归方程.
由上述步骤可以看出:主成分回归是先通过求特征值和特征向量,再降维来解决多重共线性问题的.在降维前指标之间的多重共线性可能是由于某个指标或者少数指标所包含的信息与其他指标所包含的信息之间的相关性引起的,所以通过主成分方法的降维处理,就像是把指标体系所包含的信息分了类,某一大类由一个主成分来表现,这样就消除了产生多重共线性问题的根源信息的交迭[4].
2 统计软件SPSS17.0对计算过程的实现
本文将2007—2011年每天脑卒中发病人数看作因变量y,将平均气压x1、最高气压x2、最低气压x3、平均温度x4、最高温度x5、最低温度x6、平均相对湿度x7、最低相对湿度x8,这8个环境因素看作自变量进行分析.共收集了1 461组数据.
2.1 数据标准化
在SPSS17.0软件中执行:“分析→描述统计→描述”,将变量y,x1,x2,…,x8选入“变量”对话框中,选定“将标准化得分另存为变量(Z)”,确定后,即将标准化后的数据作为变量保存(见表1).表1显示各变量的样本数(N)、均数和标准差、有效的N(列表状态).以便对标准化的自变量进行主成分回归后还原为原始变量.
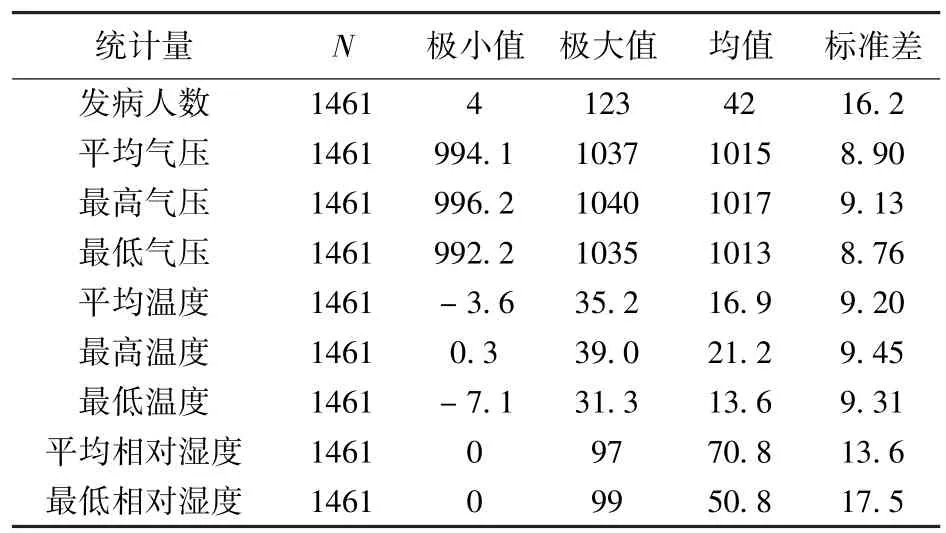
表1 描述统计量
2.2 共线性诊断
2.2.1 共线性诊断指标
共线性就是对自变量观测数据构成的矩阵X′X进行分析,使用各种指标反映自变量间的相关性.进行共线性诊断的方法有很多,目前较为常用的诊断方法有:容许度(Tolerance)、方差膨胀因子(VIF)、条件指数(Condition index)、方差比例(Variance Proportions)、特征值(Eigen values)等.
1)容许度(Tolerance)
容许度定义为Toli=1-R2i,其值介于0-1之间.其值越小,自变量xi与其它自变量xj(i≠j)之间的共线性越强.使用容许度作为共线性度量指标的条件比较严格,观测量一定要大致近似于正态分布.
2)方差膨胀因子(VIF)
方差膨胀因子(VIF)定义为VIFi=1/(1-R2i),是容许度的倒数,其值介于1-∞之间.其值越大,自变量之间存在共线性的可能性越大.
3)条件指数(Condition Index)
4)方差比例(Variance Proportions)
判断变量之间是否存在共线性,需要观测同一序号的特征值对应的变量的方差比例.比例越大,其共线性的几率越大.
5)特征值(Eigen values)
如果若干特征值较小并且接近0,表明某些变量之间存在很高的相关性.这些变量的观测量出现较小的变化时,都会导致方程系数发生较大变化.
通过单因素分析发现,脑卒中发病与自变量的相关性非常小,且无规律可寻,需要进行多因素分析,可以通过多元线性回归进行尝试.但是,部分自变量之间又存在很强的相关性,如从表2(相关系数表)中可以看出关于温度的三个指标之间的相关系都大于0.9,相关系数很大,说明共线性很强,适合用主成分回归分析讨论脑卒中发病与环境因素的问题[3].
2.2.2 共线性问题的解决方法
执行:“分析→降维→因子分析”,将8个自变量选入“变量”栏中,在“相关矩阵”栏中选中“系数”.从相关系数矩阵(表2)得到平均温度和最高温度、最低温度之间的相关系数分都是0.984;平均气压和最高气压、最低气压之间的相关系数分别为:0.991和0.990,相关系数很接近于1,说明这些变量间相关性很强.其他结果见表2.
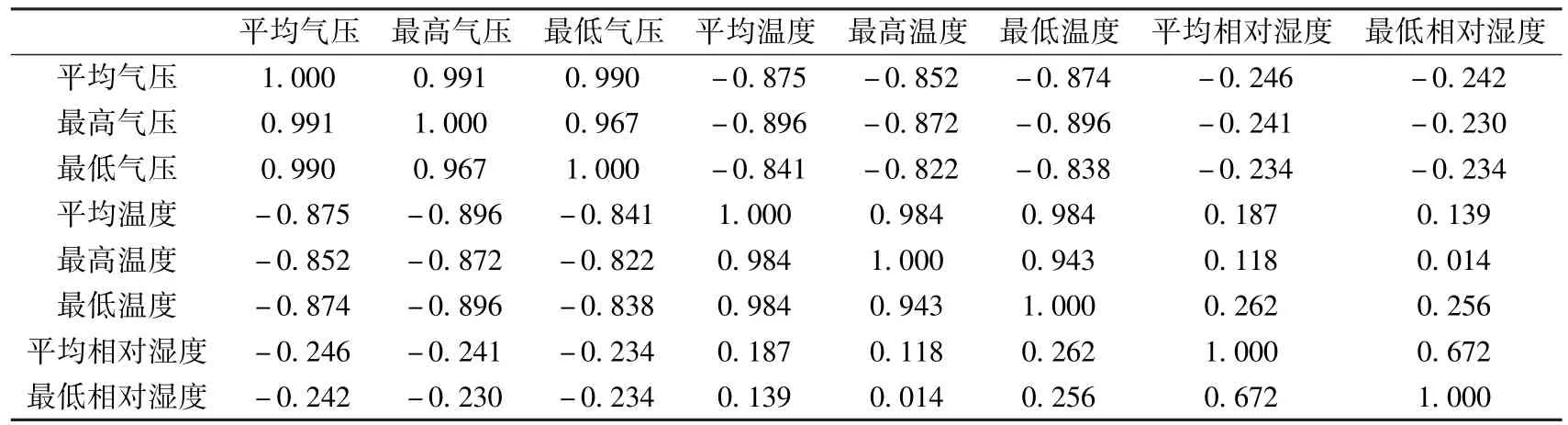
表2 相关系数表
共线性诊断也可以执行:“分析→回归→线性”,在自变量栏中导入标准化后的自变量Zx1,Zx2,…,Zx8,在“统计量”一栏中选择“共线性诊断”,其他设为默认,结果见表3.条件指数从第5个开始,远远大于30,说明存在严重共线性.表中平均气压,最高气压,最低气压,平均气温,最高气温,最低气温的容忍度都<0.1,并且其方差膨胀因子VIF都很大,说明这些变量之间存在严重的共线性.适合用主成分分析解决此问题.
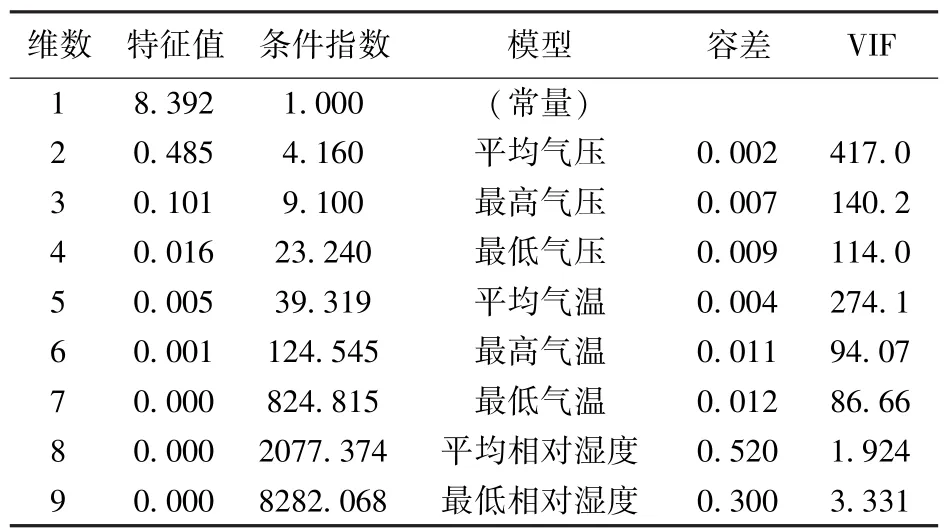
表3 共线性诊断指标(共线性统计量)
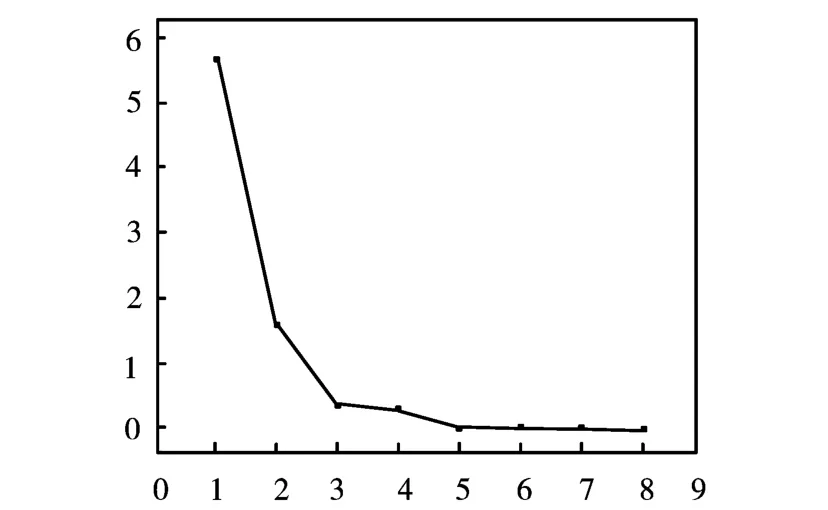
图1 特征值碎石图
2.3 主成分分析
执行:“分析→降维→因子分析”,选定标准化后的变量Zx1,Zx2,…,Zx8进入“变量”栏中,在“抽取→方法→主成分”,在提取因子数后面框中填入3,提取三个主成分,在“输出”栏中,选中“碎石图”.在“得分”中选择“保存为变量”;“方法”栏中选择“回归”.在“旋转”栏中,选择“无”.结果见图1(特征值碎石图)和表4(解释的总方差).
前3个特征根之和已经达到95.48%,所以选取3个主成分是合适的.图1为各成分特征值的碎石图,分析碎石图可以看出成分1与2,成分2与3的特征值之差值比较大.而其余成分之间的特征值差值均较小.拐点在第3个,因此提取3个因子比较合适.
前3个特征值分别为:λ1=5.668,λ2=1.588,λ3=0.387.
2.3.1 主成分分析
利用统计软件SPSS17.0对标准化后的自变量执行上述步骤,进行主成分分析,即可得到成分矩阵和成分得分系数矩阵,结果见表5.根据表5的结果计算特征向量,记特征向量Φ=(φ1,φ2,φ3).
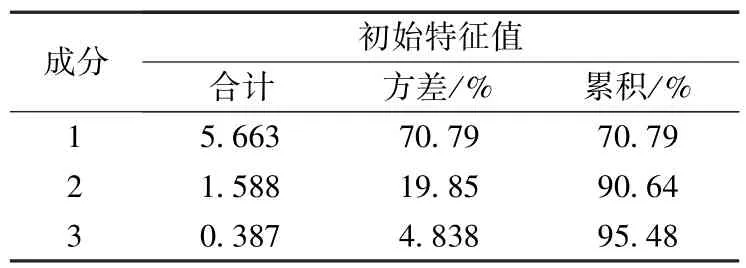
表4 解释的总方差

表5 成分矩阵和成分得分系数矩阵
2.3.2 计算特征向量
1)计算特征向量方法1,利用成分矩阵计算:
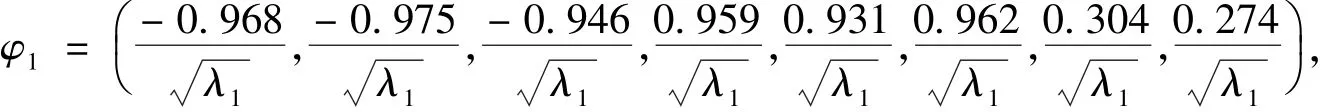
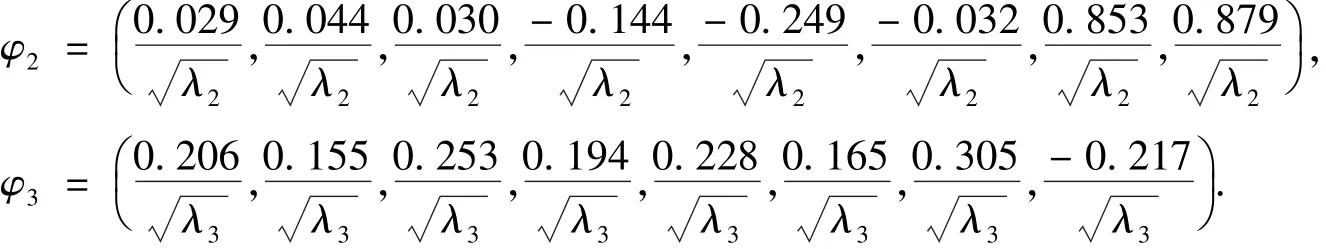
2)计算特征向量方法2,利用成分得分系数矩阵计算:

2.3.3 计算主成分
主成分Z=Φ·Zx(Zx为标准化自变量)

在excel表格中利用矩阵乘法,计算出来Z1,Z2,Z3之后跟Zy(标准化因变量)进行最小二乘回归,得到回归方程Zy=-0.052Z2,并对最终结果进行检验.确定出发病人数和各个因素最终的数学模型.根据

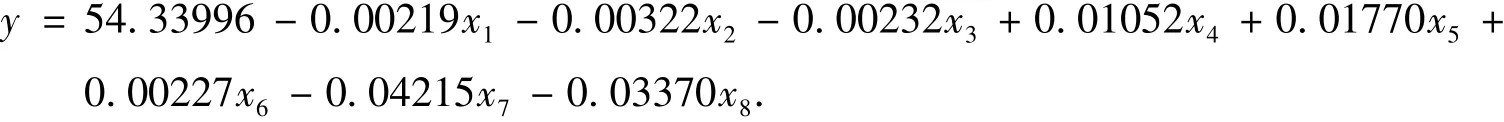
最终确定了脑卒中发病人数与环境因素之间关系的数学模型.
3 小结
主成分分析能把相关性较强的自变量综合在同一个主成分中,所计算的主成分之间彼此独立.这样把相关自变量变换为相互无关的主成分后,再结合累计方差百分比,就能够充分利用原有的信息,把主成分回归方程转换为线性回归方程,这样,既克服了共线性的干扰,又不损失原有信息.利用SPSS进行主成分回归分析是一种行之有效且快捷的方法.同时绝大部分的计算过程由计算机完成,减少人工计算的繁琐,从而获得高效、简洁和准确的统计结果[6].
在查阅文献的过程中,发现有许多文献在对主成分计算、回归和还原变量的过程中存在有概念模糊,甚至出现错误的现象.因此,本文给出了计算特征向量、主成分回归、还原原始变量过程的详细说明.
本文对脑卒中发病与环境因素之间的关系给出了相应的数学模型.虽然从脑卒中疾病本身而言,高血压,糖尿病,心脏疾病,血脂代谢紊乱、吸烟与酗酒、肥胖、等也是导致发病的直接原因,但不属于2012年全国大学生数学建模赛题(脑卒中发病环境因素分析及干预)的研究范围.
[1] 薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2001:259.
[2] 何燕.主成分回归与偏最小二乘回归方法比较[J].成都电子机械高等专科学校学报,2003(4):55-61.
[3] 郭呈全,陈希镇.主成分回归的SPSS实现[J].统计与决策,2011(5):22-28.
[4] 周松青.解决多重共线性问题的线性回归方法[J].江苏统计,2000(11):12-16.
[5] 卢纹岱.SPSS for Windows统计分析[M].北京:电子工业出版社,2005:298.
[6] 刘润幸.利用SPSS进行主成分回归分析[J].中国公共卫生,2001(8):44-50.
Principal Component Regression In⁃depth Analysis on Stroke Incidence and Environmental Factors
FEINi⁃na1,2,YANG You⁃long2
(1.Higher Colleges of Technology,Xi'an University of Technology,Xi'an Shanxi710082,China)(2.School of Mathematics and Statistics,Xidian University,Xi'an Shanxi710071,China)
Evoked brain stroke has been confirmed with environmental factors,including the existence of a close relationship between temperature and humidity.The incidence of environmental factors on stroke analysis to evaluate the risk of disease,can also be on stroke in high⁃risk groups to intervene timely.While the average pressure,maximum pressure,minimum pressure,average temperature,maximum temperature,minimum tem⁃perature,averageminimum relative humidity relative humidity between 8 variables,serious collinearitymakes using the regression equation ofmultiple linear regression method to get the accuracy greatly reduced.Princi⁃pal component regression analysis(principal component analysis and multiple linear regression combined)is an improved regression method,can eliminate the adverse effects brought by multiple correlation regression model.Using thismethod,the stroke incidence and environmental factors of in⁃depth analysis,combined with the statistical analysis software SPSS,the correct expression for calculating the principal component is given,to overcome themany false and misleading the principal components analysis using SPSS software,textbooks and published articles.Then the principal componentswith the incidence ofmultiple linear regression,and ul⁃timately determine the number ofmathematicalmodels of stroke and 8 environmental factors.
brain stroke incidence rate;environment factor;principal components regression;mathematical model
O212.4
A
1671⁃6876(2014)03⁃0200⁃06
[责任编辑:李春红]
2014⁃05⁃09
国家自然科学基金资助项目(61075055)
费妮娜(1979⁃),女,陕西西安人,讲师,西安电子科技大学博士研究生,研究方向为多元统计和因果推理. E⁃mail:feinina2010@126.com
