一类三阶m点边值问题多重正解的存在性

刘 洋，解大鹏，杨 刘

（合肥师范学院数学统计学院，安徽合肥 230601）

一类三阶m点边值问题多重正解的存在性

刘 洋，解大鹏，杨 刘

（合肥师范学院数学统计学院，安徽合肥 230601）

应用一个新的不动点定理，讨论了一类三阶m点边值问题多重正解的存在性.

边值问题；不动点定理；正解

0 引言

近年来，微分方程边值问题解的存在性与多重性在数学与工程科学方面引起了人们较大的兴趣，国内外许多学者对二阶，三阶乃至高阶的方程进行了研究，得出了大量有价值的结果［1⁃6］．如文［6］研究了非线性三阶三点边值问题

正解的存在性．本文将考虑形如

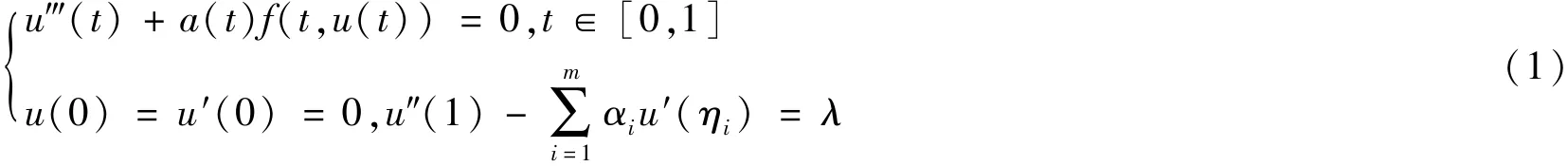
（H1）f：［0，1］×［0，∞）→［0，∞）是连续的；

（H2）a：［0，1］→［0，∞）是连续的，并且在［0，1］上不恒等于零．

1 预备知识和引理

为了证明本文的主要结果，我们给出如下的预备知识和引理

定义1 映射φ被称为P上的非负连续凹泛函，只要φ：P→［0，∞）连续且

φ（tx＋（1－t）y）≥φt（x）＋（1－t）φ（y），

对所有的x，y∈P以及0≤t≤1成立．类似地，映射ϕ被称为P上的非负连续凸泛函，只要φ：P→［0，∞）连续且

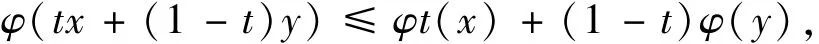
对所有的x，y∈P以及0≤t≤1成立．

定义2 给定常数r＞a＞0，L＞0．设φ是P上的非负连续凹泛函，γ，β是P上的非负连续凸泛函．定义凸集

以下假设P上非负连续凸泛函γ，β满足

（A1）存在M＞0，使得对任意x∈P有‖x‖≤M max｛γ（x），β（x）｝；

（A2）P（γ，r；β，L）＝Ø，对任意的r＞0，L＞0P⊂E．

引理1［7］令E是空间，P是一个锥，给定常数r2≥d＞b＞r1＞0，L2≥L1＞0．假定γ，β_是P上的非负连续凸泛函_且满足（A1），（A2），φ是P上的非负连续凹泛函且φ（y）≤γ（x），对所有x∈P（γ，r2；β，L2）成立．令T：P（γ，r2；β，L2）→P（γ，r2；β，L2）是全连续算子．假设

则T在P（γ，r2；β，L2）中至少有3个不动点x1，x2，x3，且有

引理2 假设则边值问题

有唯一解

其中

证明 由常规计算可证得，这里略去．

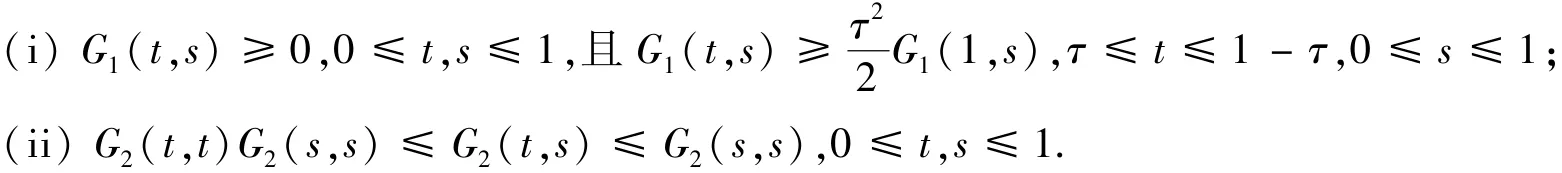
证明 由常规计算可证得，这里略去．

2 主要结果

令E＝C1［0，1］是一个Banach空间，并且定义其范数为令P是E上的锥，定义为

定义算子T：

显然边值问题（1）有解u＝u（t）当且仅当u是（2）式定义的算子T的不动点．定义泛函

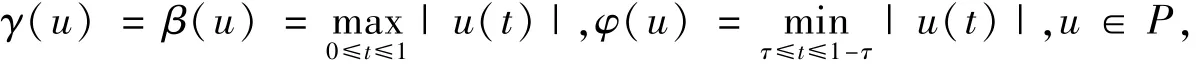
则γ，β，φ：P→［0，∞）是三个非负连续泛函，满足‖u‖＝max｛γ（u），β（u）｝＝γ（u）＝β（u），且（A1），（A2）成立，φ是凹泛函且φ（u）≤γ（u），对所有u∈P．令

使得

定理1 假设（H1），（H2）成立，假设存在常数

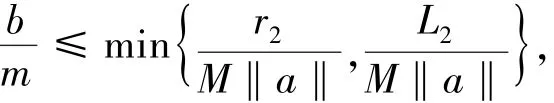
且如下假设成立：

证明 由（H1），（H2），引理3及（2）式知，T（u）≥0，u∈P，t∈［0，1］，且

因此，T（P）⊂P．并且由Arzela⁃Ascoli定理易知算子T是全连续的．下面我们验证引理1的所有条件都满足．

如果u∈P（γ，r2；β，L2），那么γ（u）＝β（u）＝0m≤a

t≤x1｜u（t）｜≤min｛r2，L2｝≤r2，从而由（H5）知，

最后验证验证引理1的条件（C3）成立，假设则由φ的定义及Tu∈P，有

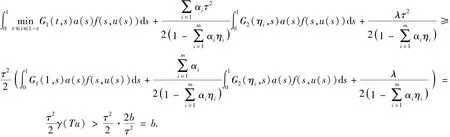
于是，引理1的条件（C3）也成立．因此由引理1知边值问题（1）至少有3个正解u1，u2，u3满足

［1］ Guo L J，Sun J P，Zhao Y H.Existence of positive solution for nonlinear third⁃order three⁃point boundary value prob⁃lem［J］.Nonlinear Anal，2008，68（10）：3151-3158.

［2］ Bai Z，Fei X.Existence of triple positive solutions for a third order generalized right focal problem［J］.Math Inequal Appl，2006，9（3）：437-444.

［3］ Ma R.Multiplicity results for a third order boundary value problem at reonance［J］.Nonliear Analysis，1998，32（4）：493-499.

［4］ Sun Y.Positive solutions of singular third order boundary value problem［J］.Math Anal Appl，2005，306：589-603.

［5］ Xie D P，Liu Y，Bai C Z.Existence ofmultiple positive solutions of higher ordermulti⁃point nonhomogeneous boundary value problem［J］.Electronic Journal of Qualitative Theory of Differential Equations，2010，33：1-13.

［6］ 解大鹏，李东.一类三阶三点边值问题正解的存在性［J］.淮阴师范学院学报：自然科学版，2007，6（3）：192-195.

［7］ Bai Z，Ge W.Existence of three positive solutions for some second⁃order boundary⁃value problems［J］.Comput Math Appl，2004，48：699-707.

Existence of M ultiple Positive Solutions for a Class of Third⁃order m⁃point Boundary Value Problem

LIU Yang，XIE Da⁃peng，YANG Liu
（School of Mathematics and Statistics，Hefei Normal University，Hefei Anhui230601，China）

By using a new fixed⁃point theorem，we establish the existence ofmultiple positivesolutions for a class of third⁃order m⁃point boundary value problem.

boundary value problem；fixed point theorem；positive solutions

O175.8

A

1671⁃6876（2014）03⁃0189⁃05

［责任编辑：李春红］

2014⁃05⁃08

国家自然科学基金资助项目（11201109）；安徽省高校省级优秀青年人才基金项目（2012SQRL165）

刘洋（1983⁃），女，吉林长春人，讲师，硕士，主要从事非线性泛函分析及其应用研究.E⁃mail：dapengx＠hftc.edu.cn