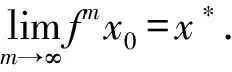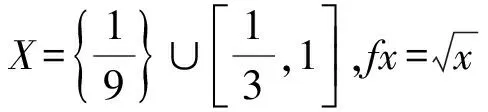Riech型Edelstein不动点定理
2023-01-16鲁书敏
鲁书敏,贺 飞,路 宁
(内蒙古大学数学科学学院,内蒙古 呼和浩特 010021)
1 预备知识
Banach不动点定理[1]在不动点理论中占据着非常重要的位置.1969年,Kannan[2]给出一种不同于Banach型的不动点定理,后人称之为Kannan型不动点定理.之后,许多学者研究了不同空间下的Kannan型不动点定理[3-7].1971年,Riech[8]建立一类不动点定理,它是Banach型和Kannan型不动点定理的统一.
1961年,Edelstein[9]在距离空间中引入ε-可链的概念,并且在ε-可链的距离空间中建立了一类不动点定理,后人称之为Edelstein不动点定理(Banach型).这一结果可以应用于解决复变量的解析函数的不动点的存在性和唯一性问题.之后许多学者讨论了Edelstein不动点定理[10-13].
定义1[9]设(X,d)是距离空间.对x,y∈X,若存在l∈和有限集{ξ0,ξ1,…,ξl}⊂X,使得
x=ξ0,y=ξl,且d(ξi-1,ξi)<ε,i=1,2,…,l,
则称x与y是ε-可链的,其中l称为链长.若X中任意两点都是ε-可链的,则称距离空间(X,d)是ε-可链的.
定理1[9]设(X,d)是完备的距离空间,f:X→X是自映射且ε>0.若(X,d)是ε-可链的且存在λ∈[0,1),使得
(x,y)∈X×X,d(x,y)<ε⟹d(fx,fy)≤λd(x,y),
则f有唯一不动点.
文献[9]认为Edelstein型不动点定理比Banach不动点定理更宽泛,但事实并非如此.事实上,虽然Edelstein不动点定理的压缩条件比Banach型不动点定理的条件弱,但是定理1要求空间是ε-可链的.下面的例子可以应用Banach型不动点定理但不能应用Edelstein不动点定理证明不动点存在.
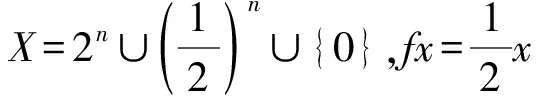
d(x,y)=|x-y|.
显然(X,d)是完备的距离空间.对任意的ε>0,取n0满足2n0>ε,x0=2n0+1,y0=2n0.可以证明,对任意的x∈X,d(x0,x)≥2n0>ε,故x0与y0不是ε-可链的,从而(X,d)不是ε-可链的.因此,在(X,d)上不可以应用Edelstein不动点定理.对于任意的x,y∈X,
故由Banach型压缩映射的不动点定理可得,f有唯一不动点x*.事实上,0是f的唯一不动点.
本文建立了Riech型Edelstein不动点定理.由此推出了Banach型Edelstein不动点定理和Kannan型Edelstein不动点定理.特别地,减弱了空间是ε-可链的条件,使得Riech型Edelstein不动点定理可以推出Riech不动点定理.同时,修改后的Edelstein不动点定理可以推出最初的Banach不动点定理.最后给出一个例子可以应用修改后的Edelstein不动点定理,但不能应用Banach不动点定理.
2 主要结果
定理2 设(X,d)是完备的距离空间,f:X→X是自映射且ε>0.假设存在x0∈X,使得x0与fx0是ε-可链的且链长为l.若存在α,β,γ≥0且α+l(β+γ)<1,使得
(x,y)∈X×X,d(x,y)<ε⟹d(fx,fy)≤αd(x,y)+βd(x,fx)+γd(y,fy),
(1)
则f有不动点.
证明设x0∈X满足x0与fx0是ε-可链的,则存在有限集{ξ0,ξ1,…,ξl}⊂X,使得
x0=ξ0,fx0=ξl,且d(ξi-1,ξi)<ε,i=1,2,…,l.
由(1)式可得
由此可得
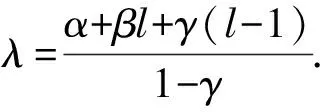
由此可得
类似地,对于i=1,2,…,l,由(1)式可得
由此可得,对于i=1,2,…,l,
(2)
下面用数学归纳法证明对于i=1,2,…,l和任意的m∈,
d(fmξi-1,fmξi)≤λmε<ε.
(3)
当m=1时,由(2)式可得(3)式成立.假设对于i=1,2,…,l,d(fmξi-1,fmξi)≤λmε<ε成立,下证(3)式对于m+1成立.由(2)式可得
由此可得,对于i=1,2,…,l,
因此由数学归纳法可得(3)式成立.
下证{fmx0}是Cauchy列.由三角不等式,
对于任意的m,n∈且m 因此{fmx0}是Cauchy列. d(fm+1x0,fx*)≤αd(fmx0,x*)+βd(fmx0,fm+1x0)+γd(x*,fx*). 令m→∞,可以得到 d(x*,fx*)≤αd(x*,x*)+βd(x*,x*)+γd(x*,fx*)=γd(x*,fx*). 由于γ>1,故d(x*,fx*)=0,即x*是f的不动点. 定理3 假设定理2的条件成立.若f的任意两个不动点x,y是ε-可链的且链长p≤l,则f存在唯一的不动点. 证明由定理2可知,f存在不动点x.下证不动点是唯一的.设y是f的不动点,则存在有限集{η0,η1,…,ηp}⊂X使得 x=η0,y=ηp,且d(ηi-1,ηi)<ε,i=1,2,…,p. 下证对于任意的m∈,对于i=1,2,…,p,有 d(fmηi-1,fmηi)≤μmε<ε, (4) 当m=1时,先证p为奇数时,(4)式成立. d(fηi-1,fηi)≤αd(ηi-1,ηi)+βd(ηi-1,fηi-1)+γd(ηi,fηi)≤ αd(ηi-1,ηi)+β[d(ηi-1,ηi-2)+…+d(η1,η0)+d(η0,fη0)+d(fη0,fη1)+…+ d(fηi-2,fηi-1)]+γ[d(ηi,ηi-1)+…+d(η1,η0)+d(η0,fη0) +d(fη0,fη1)+…+d(fηi-1,fηi)]≤ [α+2β(i-1)+γ(2i-1)]ε+γd(fηi-1,fηi). 由此可得 (5) d(fηi-1,fηi)=d(fηi,fηi-1)≤αd(ηi,ηi-1)+βd(ηi,fηi)+γd(ηi-1,fηi-1)≤ αd(ηi,ηi-1)+β[d(ηi,ηi+1)+…+d(ηp-1,ηp)+d(ηp,fηp)+ d(fηp,fηp-1)+…+d(fηi+1,fηi)]+γ[d(ηi-1,ηi)+…+d(ηp-1,ηp)+ d(ηp,fηp)+d(fηp,fηp-1)+…+d(fηi,fηi-1)]≤ [α+2β(p-i)+γ(2p-2i+1)]ε+γd(fηi,fηi-1). 由此可得 (6) d(fηi-1,fηi)≤αd(ηi-1,ηi)+βd(ηi-1,fηi-1)+γd(ηi,fηi)≤ αd(ηi-1,ηi)+β[d(ηi-1,ηi-2)+…+d(η1,η0)+d(η0,fη0)+d(fη0,fη1)+…+ d(fηi-2,fηi-1)]+γ[d(ηi,ηi+1)+…+d(ηp-1,ηp)+d(ηp,fηp)+ d(fηp,fηp-1)+…+d(fηi+1,fηi)]≤[α+β(p-1)+γ(p-1)]ε≤με. (7) 因此,当m=1且p为奇数时,(4)式成立. 再证,当m=1且p为偶数时,(4)式成立. (8) (9) 因此,当m=1且p为偶数时,(4)式成立. 综上可得,当m=1时,(4)式成立. 当m=2时,先证p为奇数时,(4)式成立. d(f2ηi-1,f2ηi)≤[α+β(p-1)+γ(p-1)]με≤μ2ε. 因此,当m=2且p为奇数时,(4)式成立. 再证,当m=2且p为偶数时,(4)式成立. 因此,当m=2且p为偶数时,(4)式成立. 综上可得,当m=2时,(4)式成立. 继续上述过程,可以得到,对任意的m∈,对于i=1,2,…,p,(4)式成立. 下证x=y.对任意的m∈,由(4)式可得 故d(x,y)=0,即x=y.因此x是f的唯一不动点. 在定理3中,令β=γ=0可以得到下面的推论. 推论1 设(X,d)是完备的距离空间,f:X→X是自映射且ε>0.假设存在x0∈X,使得x0与fx0是ε-可链的且链长为l.若存在α∈[0,1),使得 (x,y)∈X×X,d(x,y)<ε⟹d(fx,fy)≤αd(x,y), 则f有不动点.进一步地,若f的任意两个不动点x,y是ε-可链的且链长p≤l,则f的不动点唯一. 注1 推论1可以推出原始的Edelstein不动点定理,也可推出Banach不动点定理.显然推论1可推出定理1.下证推论1可推出Banach不动点定理. 对任意的y0∈X,由Banach不动点定理的压缩条件可得,对任意的n∈, d(fny0,fn+1y0)≤λd(fn-1y0,fny0)≤λ2d(fn-2y0,fn-1y0)≤…≤λnd(y0,fy0)→0(n→∞), 故对ε>0,存在N∈,使得d(fNy0,fN+1y0)<ε.取x0=fNy0,则 d(x0,fx0)=d(fNy0,fN+1y0)<ε, 从而x0和fx0是ε-可链的且链长l=1.设x,y是f的不动点,则由压缩条件可得 d(x,y)=d(fx,fy)≤λd(x,y). 由于0≤λ<1,故d(x,y)=0<ε,即不动点x,y是ε-可链的且链长p=1=l.由推论1可得,f有唯一不动点. 在定理3中,令α=0,β=γ可以得到下面的推论. (x,y)∈X×X,d(x,y)<ε⟹d(fx,fy)≤β[d(x,fx)+d(y,fy)], 则f有不动点.进一步地,若f的任意两个不动点x,y是ε-可链的且链长p≤l,则f的不动点唯一. 在推论2中,令l=1可以得到下面的推论: (x,y)∈X×X,d(x,y)<ε⟹d(fx,fy)≤β[d(x,fx)+d(y,fy)], 则f有不动点.进一步地,若f的任意两个不动点x,y是ε-可链的且链长p≤l,则f的不动点唯一. 注2 推论3可以推出Kannan型不动点定理. 下面的例子可以用推论1证明不动点存在,但是不能应用Banach不动点定理证明不动点存在. 又由于X中的任意两点都是ε-可链的,故由推论1可得,f有唯一不动点.