拟合洛伦兹曲线分析收入分配制度

徐 慈

（南京财经大学应用数学学院，江苏南京 210023）

拟合洛伦兹曲线分析收入分配制度

徐 慈

（南京财经大学应用数学学院，江苏南京 210023）

利用Matlab和给定的数据对洛伦兹曲线模型进行拟合来确定模型中的参数.通过对已有模型的分析及其中的系数进行扰动处理，建立新的L（p）模型.采用Lingo软件求出所建新模型的均方误（MSE）、平均绝对误差（MAE）以及最大绝对误差（MAS），并且与原模型进行比较，从而证明所建新模型的优点.

收入分配；洛伦兹曲线；基尼系数；曲线拟合

0 引言及预备知识

若一个国家的收入分配可以用统计分布表示，记收入分配的密度函数f（x），其中x≥0表示收入（仅考虑正的收入），x0是众数点，m是中位数点，μ是平均收入．则根据收入分配经验分析，通常有

（1）记对应的分布函数为F（x），则p＝F（x）表示收入低于或等于x的人口比例，则显然有即收入大于或等于平均收入的人口一定不到半数．

记收入低于或等于x的人口群体拥有收入占总收入的比例为L（p），则应有

L（p）称为收入分配的洛伦兹曲线．显然，L（p）越大，对应的收入分配显然更优．下图中红色曲线是某收入分配的洛伦兹曲线．

其中横轴表示人口比例，纵轴表示总收入比例．显然，图中曲线位置越高，所代表的收入分配越平等．其中45°线可以理解为平等收入线，这时，任何低收入端人口比例为p的人口拥有的总收入比例也是p，从而必定是完全平等的收入分配．因此定义45°线与L（p）之间面积的2倍为基尼系数．于是基尼系数定义为

基尼系数［1］，是国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标．它是一个比值，数值在0和1之间．基尼指数的数值越低，表明财富在社会成员之间的分配越均匀．

L（p）与f（x）具有关系

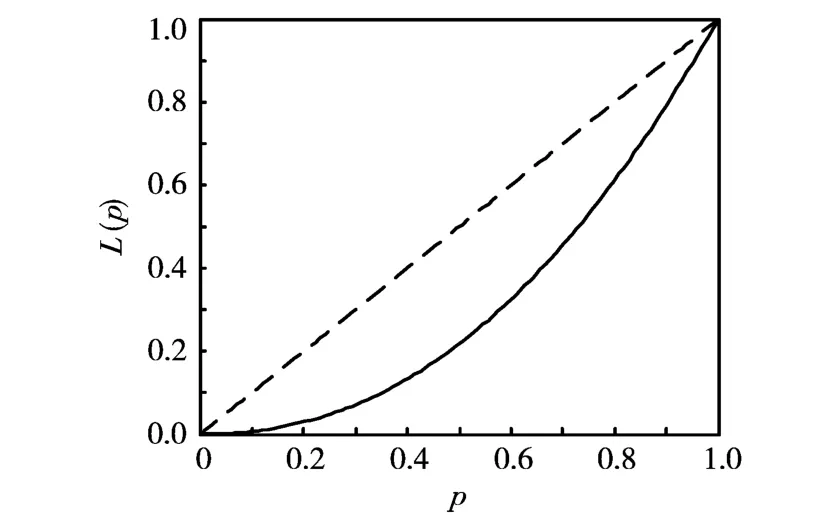
图1 某收入分配的洛伦兹曲线

其中p＝F（x），若记 F（x）的反函数为F－1（p），则洛伦兹曲线可以表示为

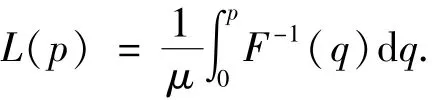
通过络伦兹曲线，可以直观地看到一个国家收入分配平等或不平等的状况．

尽管可根据收入分配的统计数据加以描绘，但至今却未能找到一种有效的方法，准确地拟合洛伦兹曲线方程并由此求出精确的基尼系数．

目前常被使用的方法主要有3种：

1）几何计算法：即根据分组资料，按几何图形分块近似逼近计算的方法．

2）间接拟合法：即先拟合求出收入分配的概率密度函数，再根据概率密度函数导出洛伦兹曲线．

3）曲线拟合法：即选择适当的曲线直接拟合洛伦兹曲线，常用的曲线有二次曲线、指数曲线和三角函数曲线等．

利用第1种方法不能得到洛伦兹曲线的表达式，只能用来计算基尼系数，但由于在计算分块面积时用直线近似地代替曲线，所估计的基尼系数要小于实际值，尤其在数据点较少时，误差较大．第2种方法由于计算收入分配的概率密度的复杂性，较难提出合适的概率函数，实践证明使用洛伦兹曲线模型是比较理想的方法之一．但目前主要的问题在于现有常用的曲线并不适用，曲线含义不明确，或拟合误差较大．

1 模型的建立

为了更准确地描述洛伦兹曲线和精确地估计基尼系数，我们首先通过入户调查获得家庭收入与消费等数据，则可以实用Kernel法估计收入分配的统计分布［3］．再通过分析洛伦兹曲线的特性，设计出一条洛伦兹曲线方程，对洛伦兹曲线直接进行拟合［4］．

由于居民收入分配关系到广大民众的生活水平，分配公平程度是广泛关注的话题，故受到许多学者的研究与分析．他们对此也建立了诸如此类的模型［5］，例如：

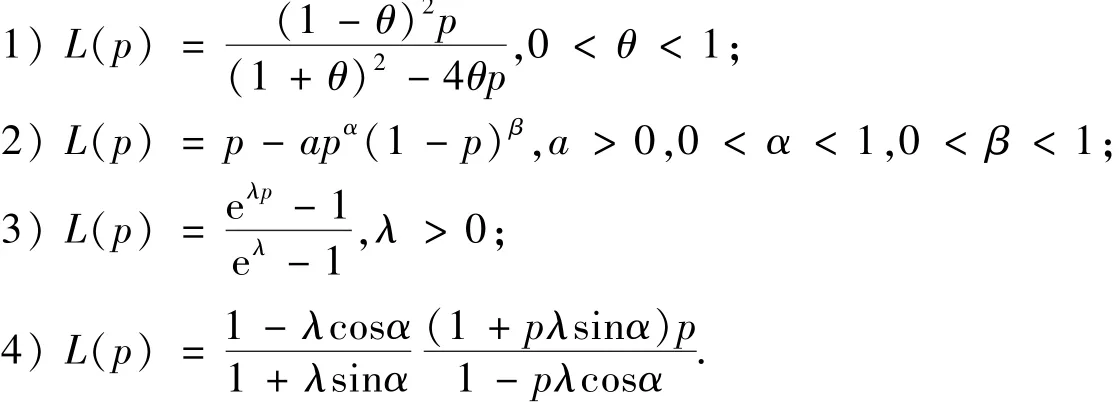
在上面已有模型L（p）＝p－apα（1－p）β，a＞0，0＜α＜1，0＜β＜1的研究分析基础上，结合实际的统计数据，再次进行基本拟合，对其中的参数进行扰动分析，可以得到更加精确的洛伦兹曲线模型，参考其思想，对上面模型中的参数通过加躁处理，利用Matlab进行，找出相对合理的扰动，建立新的模型，其模型如下：

且L（0）＝0，L（1）＝1，同时又满足洛伦兹曲线模型的条件

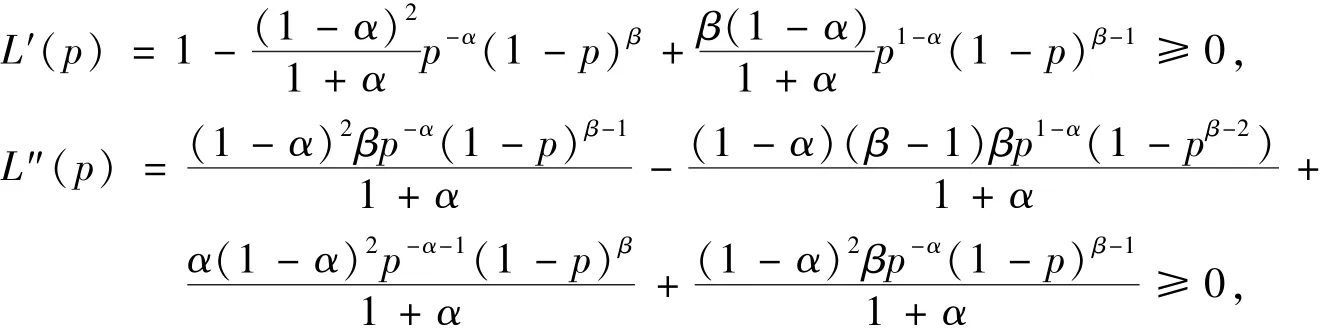
即L（p）在［0，1］上是凸增函数．

这说明了此模型具有可行性，是合理的．下验证此模型是否比原模型的拟合效果好，更具有优势．

2 实例分析

L（p）模型拟合精度的好坏，可以考虑L（p）与分组数据的拟合情况，通过综合考虑均方误差（MSE，mean squared error），平均绝对误差（MAE，mean absolute error）和最大绝对误差（MAS，maximum absolute error）的大小来判断［2］．

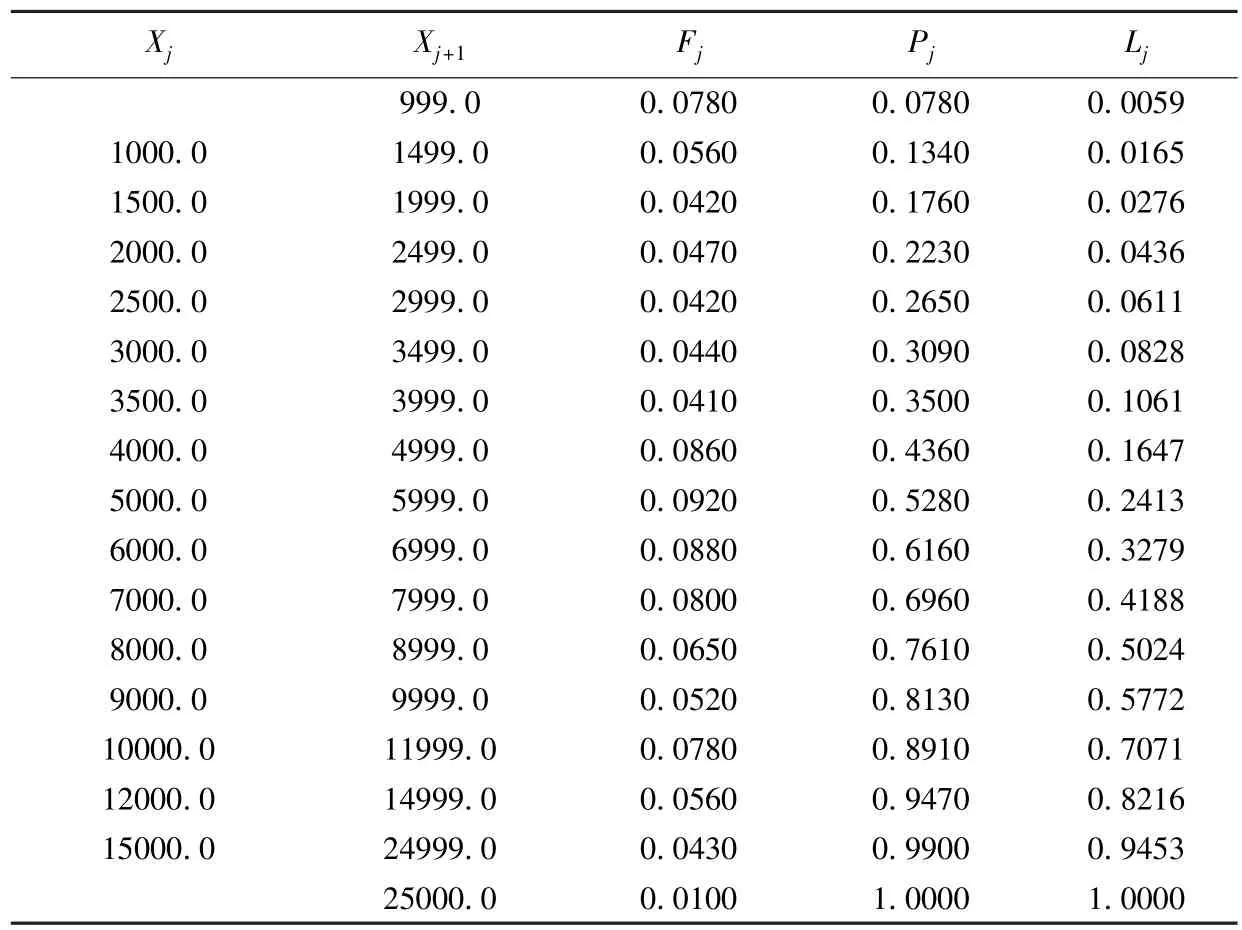
表1 收入分配分组数据

表1中［xj，xj＋1］是收入区间，单位为元，fj是该区间内的人口比例，pj是［0，xj＋1］中人口比例，Lj是［0，xj＋1］中人口拥有的总收入比例，因此（pj，Lj）是洛伦兹曲线上的点．

根据表1中给出的收入分配分组数据，利用Matlab软件对两模型分别拟合出洛伦兹曲线．如图1和图2所示．

图2 L（p）＝p－apα（1－p）β模型的拟合曲线图

图3 L（p）＝p1－p）β模型的拟合曲线图

根据表1中的收入分配分组数据，首先拟合出各自的参数，然后应用Lingo软件分别求出每个模型的MSE、MAE和MAS，将计算结果进行比较，见表2．

表2 两种模型的MSE、MAE和MAS数据比较

根据表2，可以直观的看出，新模型比原模型的3个误差值都要小，因此具有较好拟合精度．经过实例分析，新模型具有较好的拟合效果，并且由此洛伦兹曲线可推导出基尼系数，计算结果精确度也较高．

3 小结

由上面的分析可知，所建立的L（p）模型不仅要满足洛伦兹曲线，而且拟合出的洛伦兹曲线要有较高的精确度，即该文所衡量的3个误差值要尽可能的足够小，则此时根据洛伦兹曲线计算出的基尼系数才够精确．基尼系数越小，说明居民收入分配越均匀，反之，收入分配越不均匀．

根据内容三的实证分析易知，本文所建的新模型较原模型具有较好的拟合效果．它是在原模型的基础上通过对其中的参数进行扰动分析，从而得到更加精确的洛伦兹曲线模型，达到了理想的拟合效果，说明本文所建立的洛伦兹曲线模型具有较高的实用价值．

一般来讲，洛伦兹曲线反映了居民收入分配的不平等程度．弯曲程度越小，基尼系数也越小，居民收入分配越平等，反之亦然．

［1］ 宋树仁，李玲，梅立群.中国居民基尼系数的测度与计量［J］.统计与管理，2010，2（2）：149－158.

［2］ 赵人伟.中国居民收入分配研究［M］.北京：中国经济出版社，2003.

［3］ 欧阳植，于维生.分组数据的收入分布拟合及洛伦兹曲线与基尼系数［J］.数量经济技术经济研究，1994（6）：37-42.

［4］ Wang Z X，Smyth R.A hybridmethod for creating Lorenz curveswith an application tomeasuringworld income inequality［J］.Business and Economics，2013，144：13-46.

［5］ Wang Z X，Ng Y K，Smyth R.A generalmethod for creating Lorenz curves［J］.The Review of Income and Wealth，2011，57：561-582.

［6］ Chotikapanich D S，Rao P，Tang K K.Estimating income inequality in China using grouped data and the generalized Beta distribution［J］.The Review of Income and Wealth，2007，53：127-47.

The Analysis of the Income Distribution System by Fitting Lorenz Curve

XU Ci
（School of Applied Mathetics，Nanjing University of Finance and Economics，Nanjing Jiangsu 210023，China）

this paper，we determine the parameters of the Lorenz curve by using Matlab and the given data to fit Lorenz curve.And we create a new model L（p）through the analysis of the original one，in which the co⁃efficients are treated by perturbation.Then，the new model’s the mean square error（MSE），mean absolute error（MAE），and themaximum absolute error（MAS）are calculated by the Lingo software，and thus the ad⁃vantages of the new model compared with the originalmodel are proved.

income distribution；lorenz curve；gini coefficient；curve fitting

O221

A

1671⁃6876（2014）03⁃0210⁃04

［责任编辑：李春红］

2014⁃04⁃28

徐慈（1989⁃），女，安徽阜阳人，硕士研究生，研究方向为非线性分析及应用.E⁃mail：xuci1329056852＠163.com