增量动力分析地震动强度参数研究综述
2014-03-21励勐劼
周 颖 励勐劼
(同济大学土木工程防灾国家重点实验室,上海200092)
1 引言
增量动力分析(Incremental Dynamic Analysis,IDA)被称作动力推覆分析,是目前基于性能的地震工程中最具有发展前景的方法之一,已被美国联邦紧急救援署(Federal Emergency Management Agency,FEMA)所采用,作为分析钢框架结构整体抗倒塌能力的方法[1]。
增量动力分析结果是通过地震动强度参数(Intensity Measure,IM)与工程需求参数(Engineering demand parameter,EDP)关系来表示,可以反映结构历经初始弹性、逐步退化直至整体动力失稳的全过程响应。目前常用的工程需求参数,例如最大层间位移角θmax能较好反映结构破坏程度[2],具有一定的合理性[3]。而选用不同地震动强度参数将获得不同的分析结果,是影响结构抗震性能评估结果的关键因素之一[4]。近年来各国学者从不同角度对地震动强度参数进行了研究,本文从标量型地震动强度参数和向量型地震动强度参数展开分析。
2 地震动强度参数基本性质
地震动强度参数是表征地震动强度的指标,其应具有以下性质,并可作为判断地震动强度参数优劣的标准。
(1)有效性(Efficiency):有效性可降低需求中位值估计误差,减少分析所需地震动数量,可通过条件对数标准差来判别。
(2)充分性(Sufficiency):指地震动强度参数在统计意义上对地震特征参数(震级M,震中距R等)的条件独立性,通常可用P值判断。
(3)相关性(Correlation):反映地震动强度参数与工程需求参数的关联程度,可用相关系数的平方来判断。
(4)实用性(Practicality):指地震动强度参数与工程需求参数的关联敏感性。地震动强度参数实用性不强,则工程需求参数很少或者不依赖于地震动强度参数的变化。实用性通常可用线性回归系数b来判断。
(5)适用性(Proficiency):综合考虑有效性和实用性的性质。通常用条件对数标准差与线性回归系数b的比值来判断。
(6)比例鲁棒性(Scaling Robustness):指地震动强度参数按比例调整后,结构的响应结果具有的无偏性质。
(7)危险性可计算性(Hazard Computability):地震动强度参数在计算地震危险性时所应具有的简易特性。
3 标量型地震动强度参数
峰值加速度(Peak Ground Acceleration,PGA)概念直观简单,是最早使用也是目前使用最多的地震动强度参数,大多国家都采用这一指标。
在1998年,Bazzurro等[5]提出了用结构弹性基本周期对应的加速度反应谱谱值Sa(T1)作为地震动强度参数。随后Vamvatasikos等[6]在2002年对这两个参数进行了比较,认为Sa(T1)可以明显降低增量动力分析结果的离散程度。Sa(T1)也逐渐发展为目前最为常用的地震动强度参数之一。但随着研究的不断深入,发现Sa(T1)作为地震动强度参数并不完善,例如不适用于长周期结构等,从而衍生了许多改进地震动强度参数或者通过其他角度切入的地震动强度参数。
3.1 基于加速度反应谱谱形的地震动强度参数
当阻尼比确定时,地震动对应的加速度弹性反应谱的形状即确定。基于谱形的地震动强度参数实质就是将反应谱与结构关联起来,通过谱值、斜率等参数来反映地震动与结构的信息。目前的相关研究主要基于加速度反应谱Sa,原因有两点[7]:灾害危险性分布图(Hazard Maps)大多基于加速度反应谱;许多研究已经讨论了以加速度反应谱作为地震动强度参数的优缺点。将反应谱与结构特性相结合的地震动强度参数是研究与应用的主要方向。
3.1.1 基于结构非线性的地震动强度参数
Cordova等[8]在2000年提出了一个考虑非线性结构周期延长的地震动强度参数:

式中,Tf是一个大于T1的值,一般情况下可采用α=0.5和Tf/T1=2,该参数可以降低增量动力分析曲线的整体离散性。
在此基础上,Mehanny等[9]在 2009年提出了:

杨成等[10]在2010年做了两点修正:将Tf/T1的比值由2改为由静力推覆分析确定;将α取0.5改为随增量动力分析加载级别控制的渐变函数:

式中,Sa,i(T1)表示第i级增量动力分析地震输入下的结构基本周期对应的弹性反应谱值;Sa,475y(T1)表示50年超越概率10%水平下对应的规范设计反应谱值;Sa,max(T1)表示动力失稳前增量动力分析最大响应谱值。
该函数对增量动力分析曲线收敛性有一定的提高。
上述学者在考虑结构非线性周期延长均采用了延长单个周期所对应的反应谱谱值。对此,Bojórquez[11]在 2010 年提出了用多个谱值点反映周期延长段谱形的地震动强度参数:

式中,

式中,Tn取2~2.5倍的基本周期,α在0~1之间取值。
该地震动强度参数对增量动力分析曲线离散程度的降低明显优于前者提出的地震动强度参数。
3.1.2 基于高阶振型的地震动强度参数
随着结构高度的增加,周期随之增加,高阶振型影响不可忽略。Asgarian等[12]在2012年提出了基于前三阶振型的地震动强度参数:
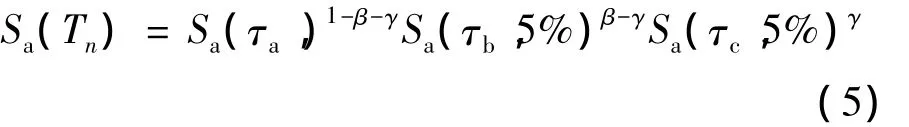
式中,τa,τb,τc为结构一个方向的前三阶周期;β=γ=1/3。
周颖等[4]在2013年提出了更进一层次的地震动强度参数:

与Asgarian等提出的地震动强度参数相比,α,β,γ用振型质量参与系数的权重表示,反映出各阶振型的影响。此外,Lu等[13]在2013年也提出了基于多阶振型的地震动强度参数:

推导了阶数n与基本周期T1的关系式,等效地对待了各阶振型。
上述基于高阶振型影响的地震动强度参数在对中长周期结构的增量动力分析曲线离散程度减小方面均得到了很好的验证。
3.1.3 基于非线性与高阶振型的地震动强度参数
除了单方面基于非线性影响和高阶振型影响的地震动强度参数外,有学者开始提出了综合考虑两者的地震动强度参数。2009年,Bianchini等[14]提出了:

与 Bojórquez 提出的 INp中的 Sa,avg(T1,…,Tn)不同,式(8a)中的Ti均不代表结构的i阶自振周期,包括T1,并非结构基本周期。该组周期点只是普通的一组周期点,但范围涵盖了结构高阶周期点与结构非线性周期延长的周期点。通过证明,对于多自由度系统Sa,avg可用10个周期点,并用系数与基本周期T(1)乘积表示,可将式(8a)写为:

式中,Kl考虑了高阶振型,为选取周期点的下限;Ku考虑了非线性周期延长,为选取周期点的上限,该系数的值可根据结构延性系数μ确定。
经过分析,Sa,avg的有效性与充分性均优于Sa(T1)。
Lin等[2]在2010年提出了针对考虑非线性和高阶振型影响的两个地震动强度参数,通过判断结构基本周期T1的范围来选择:

式中,SN1考虑了结构非线性,适用于T1<1.5 s的框架,SN2考虑了高阶振型,适用于T1>1.5 s的框架;C为考虑结构非线性的周期延长系数,根据美国土木工程学会标准7荷载规范ASCE/SEI 7 -05 建议取为 1.5[15]。
Adeli等[16]在2012年提出了一种用加速度反应谱面积表示的地震动强度参数:区间范围在[1.2Tm,1.5T1]的谱面积。其中,Tm为结构振型质量参与系数超过95%对应的周期,该区间包含了高阶振型以及非线性周期延长段。反应谱的面积可认为是一种谱强度,面积也可看作是多个谱值的叠加。
从上述研究成果中可以发现,目前基于加速度反应谱谱值的地震动强度参数研究开展的较为广泛,并逐步从单一谱值点的形式发展至多个谱值点。一般可以认为,随着地震动强度参数表达形式中反应谱谱值点的增加,所描述的反应谱谱形更为准确,同时反映出的反应谱与结构的信息也更加全面,其计算结果将更为合理。
尽管基于反应谱谱形相关研究较多,但目前仍缺乏全面反映结构特性与地震动信息的参数。在考虑结构非线性影响时,也仅从结构刚度降低、周期延长的角度出发,并未考虑阻尼等因素。这仍将会成为今后研究的主要方向。
3.2 基于位移的地震动强度参数
Luco等[17]在2007年提出了6个基于弹性位移反应谱和非弹性位移反应谱的地震动强度参数:


此外,2013年Lu等[18]在不同周期结构下对峰值位移(Peak Ground Displacement,PGD)以及位移反应谱在结构基本周期的谱值Sd(T1)进行了比较,研究发现Sd(T1)与Sa(T1)相比在离散程度上并没有降低,反而在低周期结构效果不如Sa(T1)。峰值位移在长周期结构有效性与IM1E&2E相近,优于Sa(T1),但同样也不适用短周期结构。
3.3 基于速度的地震动强度参数
目前基于速度的地震动强度参数研究主要是针对已有速度型地震动强度参数进行对比。Wang等[19]在2012年通过比较,建议用速度谱强度(Velocity Spectrum Intensity,VSI)与峰值速度(Peak Ground Velocity,PGV)作为桥基耦合系统的地震动强度参数。Asgarian等[12]在2012年对速度反应谱在结构基本周期的谱值Sv(T1)进行了比较,认为近场地震作用最合适的地震动强度参数为 Sv(T1)。此外 Lu 等[13,18]在 2013 年也对地震动峰值速度作了对比研究,发现峰值速度对长周期结构相关性与离散程度均表现优异。
从上述研究表明,基于速度的地震动强度参数相对于传统的基于加速度的地震动强度参数有一定的优势,且日本也采用峰值速度作为烈度的物理标准。但我国抗震设计采用峰值加速度作为主要参数指标,相应峰值速度的研究尚存空缺。总体来说,基于位移和速度的地震动强度参数相对基于加速度反应谱的地震动强度参数缺乏系统的研究,应值得学者关注。
3.4 基于弹塑性反应谱的地震动强度参数
杨成等[20]在2008年用弹塑性反应谱谱值NSa(T1,5%)来代替Sa(T1)作为地震动强度参数,提出改进的MIDA(Modified IDA)方法。杨成采用了Buffalo大学的NSPECTRA2.0程序计算弹塑性反应谱,并定义了弹塑性反应谱计算参数ξy。通过算例发现,用NSa(T1,5%)作为地震动强度参数得到的增量动力分析曲线离散性明显小于采用弹性反应谱Sa(T1)。
目前研究难点主要在于弹塑性反应谱的确定,基于弹塑性反应谱的地震动强度参数的研究并未得到很好的开展。
4 向量型地震动强度参数
由于一维标量型地震动强度参数存在着局限性,Baker[21]在2005 年将地震动强度参数从一维发展到了二维,提出了一种向量型地震动强度参数 <Sa(T1),ε>。其中,ε为地震动加速度反应谱谱值与衰减模型预测得到的加速度反应谱均值之间的差值,同样也是一种反映反应谱谱形的参数。通过与震级M和震中距R进行对比,ε对分析结果的影响要更大。Baker还建议在选取地震动进行分析时要考虑ε。
随后,2008 年 Baker[22]在 Cordova 等[8]基础上提出了向量型地震动强度参数 <Sa(T1),RT1,T2>,其中,RT1,T2为T1和T2周期对应的反应谱谱值的比值。研究表明,传统的Sa(T1)不能很好描述脉冲型地震动,而第二参数RT1,T2的加入使得地震动强度参数针对普通型和脉冲型地震动进行结构响应预测时没有明显区别,使地震动强度参数更具有充分性。
2011 年 Bojórquez[23]在标量型 INp[11]基础上也提出了新的向量型地震动强度参数<Sa(T1),Np>,其中,Np表达式与3.1.1节中式(4)相同。研究证明,在相同标准误差e之下,向量型地震动强度参数所需的地震动数量n明显小于标量型地震动强度参数,其中近场脉冲型地震动的数量向量型仅为标量型的10%。由此可见,选用向量型地震动强度参数可提高计算分析的效率。
随后在2012 年,Bojórquez等[7]又作了进一步的探讨,将向量型地震动强度参数划分为峰值型(< Sa(T1),PGA > 、< Sa(T1),PGV >)、累积破坏型(<Sa(T1),tD>、<Sa(T1),ID>)和基于反应谱谱形 (<Sa(T1),RT1,T2> 、<Sa(T1),Np>)三大类进行研究比较。向量型地震动强度参数第一参数均为Sa(T1),tD为地震动持时,ID=,tE为地震动总时长。结果表明基于反应谱谱形的向量型地震动强度参数 < Sa(T1),RT1,T2> 和 < Sa(T1),Np> 有效性较高。
近年有学者在原有的标量型地震动强度参数基础上进行组合。Jalayer等[24]在2012年对向量型地 震 动 强 度 参 数 <Sa(T1),Sa(T2) > 、<Sa(T1),ε>、<PGA,M >进行了对比研究,其中考虑两阶振型的 <Sa(T1),Sa(T2)>充分性较好。
Gehl等[25]在2013年研究了50个标量型地震动强度参数值(如峰值加速度、峰值速度、Arias强度等),对结构屈服与倒塌两种状况进行比较,结果未发现有标量型地震动强度参数同时属于这两种状况的最佳选择。通过用向量型地震动强度参数将原有标量型地震动强度参数进行组合,汲取单个标量型地震动强度参数优势。研究表明,二维的向量型地震动强度参数有效性均要高于一维标量型地震动强度参数,其可降低地震危险性分析的不确定性。
向量型地震动强度参数相比标量型地震动强度参数可提供更多的信息,并可将各影响因素分开考虑,相对于综合型的单一标量型地震动强度参数其意义更为明确。向量型地震动强度参数的充分性和有效性已经在研究中得到了验证,其具有一定的优势。目前向量型地震动强度研究刚刚开展,研究空间较大。
5 结语
降低增量动力分析曲线离散性,可减少地震动样本数量;提高地震动强度参数充分性,可简化地震危险性分析的积分式[22]。因此深入地震动强度参数研究对基于性能的地震工程分析的效率提高具有重要意义。目前无论是标量型地震动强度参数还是向量型地震动强度参数,基于反应谱谱形的地震动强度参数仍是研究的趋势。随着结构高度增加、体系复杂化,选取地震动强度参数时需要考虑更多的影响因素。而向量型地震动强度参数相比标量型地震动强度参数可提供的信息更多,具有更大的发展前景。此外,由于目前的研究采用的地震动输入均为单向,并不能完全满足工程要求,因此多向地震动输入的地震动强度参数研究也将是今后应重视的研究内容。
[1] Federal Emergency Management Agency.Recommended seismic design criteria for new steel momentframe buildings[R].Washington DC:2000.
[2] Lin L,Naumoski N,Saatcioglu M,et al.Improved intensity measures for probabilistic seismic demand analysis part 1:development of improved intensity measures[J].Canadian Journal of Civil Engineering,2010,38(1):79-88.
[3] 周颖,吕西林,卜一.增量动力分析法在高层混合结构性能评估中的应用.同济大学学报(自然科学版),2010,38(2):183-193.Zhou Ying,Lu Xilin,Bu Yi.Application of incremental dynamic analysis to seismic evaluation of hybrid structure[J].Journal of Tongji University(Natural Science Edition),2010,38(2):183-193.(in Chinese)
[4] 周颖,苏宁粉,吕西林.高层建筑结构增量动力分析的地震动强度参数研究[J].建筑结构学报,2013,34(2):53-60.Zhou Ying,Su Ningfen,Lu Xilin.Study on intensity measure of incremental dynamic analysis for high-rise structures[J].Journal of Building Structures,2013,34(2):53-60.(in Chinese)
[5] Bazzurro P,Cornell C A,Shome N,et al.Three proposals for characterizing MDOF nonlinear seismic response[J].Journal of Structural Engineering,1998,124(11):1281-1289.
[6] Vamvatsikos D,Cornell C A.Incremental dynamic analysis[J].Earthquake Engineering and Structural Dynamics,2002,31(3):491-514.
[7] Bojórquez E,Iervolino I,Reyes-Salazar A,et al.Comparing vector-valued intensity measures for fragility analysis of steel frames in the case of narrow-band ground motions[J].Engineering Structures,2012,45:472-480.
[8] Cordova P P,Deierlein G G,Mehanny S S F,et al.Development of a two-parameter seismic intensity measure and probabilistic assessment procedure[C].Proceedings of the 2nd US-Japan Workshop on Performance-Based Seismic Design Methodology for Reinforced Concrete Building Structures,2000.
[9] Mehanny S S F.A broad-range power-law form scalar-based seismic intensity measure[J].Engineering Structures,2009,31(7):1354-1368.
[10] 杨成,潘毅,赵世春,等.烈度指标对IDA曲线离散性的影响[J].工程力学,2010,27(增刊 I):68-72.Yang Cheng,Pan Yi,Zhao Shichun,et al.Effect of seismic intensity measure function to the IDA curves dispesion[J].Engineering Mechanics,2010,27(S I):68-72.(in Chinese)
[11] Bojórquez E,Iervolino I.A Spectral shape-based scalar ground motion intensity measure for maximum and cumulative structural demands[C].Proceedings.of 14th European Conference on Earthquake Engineering,2010.
[12] Asgarian B,Khazaee H,Mirtaheri M.Performance evaluation of different types of steel moment resisting frames subjected to strong ground motion through incremental dynamic analysis[J].International Journal of Steel Structures,2012,12(3):363-379.
[13] Lu X,Ye L P,Lu X Z,et al.An improved ground motion intensity measure for super high-rise buildings[J].Science China Technological Sciences,2013,56(6):if25-if33.
[14] Bianchini M,Diotallevi P P,Baker J W.Prediction of inelastic structural response using an average of spectral accelerations[C].10th International Conference on Structural Safety and Reliability(ICOSSAR09),Osaka,Japan.2009.
[15] ASCE/SEI 7-05.Minimum design loads for buildings and other structures[C].American Society of Civil Engineers,2006.
[16] Adeli M M,Banazadeh M,Deylami A,et al.Introducing a new spectral intensity measure parameter to estimate the seismic demand of steel moment-resisting frames using bayesian statistics[J].Advances in Structural Engineering,2012,15(2):231-248.
[17] Luco N,Cornell C A.Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions[J].Earthquake Spectra,2007,23(2):357-392.
[18] Lu X,Lu X Z,Guan H,et al.Comparison and selection of ground motion intensity measures for seismic design of super high-rise buildings[J].Advances in Structural Engineering,2013,16(7):1249-1262.
[19] Wang Z,Osorio L,Padgett J E.Optimal intensity measures for probabilistic seismic response analysis of bridges on liquefiable and non-liquefiable soils[C].Proceedings.of the 2012 Structures Congress,2012.
[20] 杨成,徐腾飞,李英民,等.应用弹塑性反应谱对IDA方法的改进研究[J].地震工程与工程震动,2008,28(4):64-69.Yang Cheng,Xu Tengfei,Li Yingmin,et al.Research on modified IDA method by inelastic response spectrum[J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(4):64-69.(in Chinese)
[21] Baker J W,Cornell C A.A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon[J].Earthquake Engineering and Structural Dynamics,2005,34(10):1193-1217.
[22] Baker J W,Cornell C A.Vector-valued intensity measures for pulse-like near-fault ground motions[J].Engineering Structures,2008,30(4):1048-1057.
[23] Bojórquez E,Iervolino I.Spectral shape proxies and nonlinear structural response[J].Soil Dynamics and Earthquake Engineering,2011,31(7):996-1008.
[24] Jalayer F,Beck J L,Zareian F.Analyzing the sufficiency of alternative scalar and vector intensity measures of ground shaking based on information theory[J].Journal of Engineering Mechanics,2011,138(3):307-316.
[25] Gehl P,Seyedi D M,Douglas J.Vector-valued fragility functions for seismic risk evaluation[J].Bulletin of Earthquake Engineering,2013,11(2):365-384.
