空间钻石型钢塔梁柱连接节点力学特性分析

陈鸿炜 苏庆田 吴 冲 孙旭霞

(1．同济大学建筑设计研究院(集团)有限公司，上海200092;2．同济大学桥梁工程系，上海200092)

1 引言

随着我国经济的迅猛发展，桥梁除了满足结构安全、经济适用外，人们越来越重视桥梁艺术和美学，一大批结构形式新颖、造型别致的桥梁相继建成。其中，斜拉桥异形钢桥塔就是有别于传统桥塔的一种新颖的结构形式［1，2］。异形斜拉桥除了具有一般斜拉桥的共性之外，还有自身独特的特点。这些异形桥塔构造复杂、传力机理不明确，传统的杆系计算理论是否可以满足设计要求存在疑问。目前在建筑结构中对于梁柱连接节点研究较多［3-8］，而对于桥梁结构空间异形塔的梁柱连接节点研究较少。本文结合范蠡大桥对桥塔的梁柱节点分析其受力特点，得到的相关结论可为类似工程参考。

2 工程背景

背景工程范蠡大桥是一座全钢结构三塔单索面斜拉桥，跨径布置为(82+168+168+82)m，如图1所示。该桥桥塔为空间钻石形，由4根塔柱构成，如图2所示。塔柱为钢结构八边形截面，四根塔柱之间采用上、中、下三组横梁相连。范蠡大桥桥塔中每个塔柱的上下塔柱交汇处分别与两道横梁相连。上下塔柱的轴线斜交，上下塔柱交汇点同时又要连接两道截面形式为四边形的横梁;采用钢板围成的箱形塔柱和横梁内部还需布置加劲肋和隔板，该部位的板件空间错落交汇，结构形式复杂。梁柱连接节点是把上塔柱的力传到下塔柱的关键部位，由于上下塔柱的轴线斜交，使得该部位的板件受力极其复杂。

图1 范蠡大桥总体布置图(单位:m)Fig．1 General layout of Fanli Bridge(Unit:m)

图2 范蠡大桥桥塔构造图及梁柱节点构造图(单位:mm)Fig．2 Pylon and beam-column joint structure details(Unit:mm)

3 计算模型

为了分析梁柱节点的受力性能，采用大型通用有限元程序ANSYS建立全桥杆系模型，如图3(a)所示，以及中间桥塔的空间板壳有限元模型，如图3(b)所示，其中梁柱节点的详细局部模型，如图3(c)所示。模型采用BEAM188单元模拟全桥、SHELL63单元模拟塔柱。模型中钢材弹性模量取2．1 ×108kN/m2，容重取 78．5 kN/m3。

荷载取最不利荷载组合进行验算，单根拉索索力如表1所示。表中锚箱编号1～9分别是塔柱从上到下的9个锚箱编号。将斜拉索与平行索的索力以面荷载的形式施加于锚箱承压板上。考虑锚箱承压板对应力的扩散作用，荷载作用于承压板圆环面积上。边界条件是将塔柱底部固结。

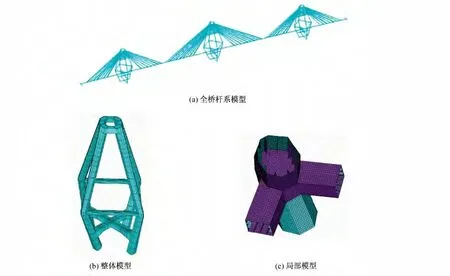
图3 结构模型示意图Fig．3 Structure model

表1 最不利荷载组合索力Table 1 The most undesirable cable forces kN

4 计算结果

4．1 塔柱受力分析

塔柱各个板件编号如图4所示，其中UW代表梁柱节点上塔柱，DW代表梁柱节点下塔柱。斜拉桥索力通过节点上塔柱传递至梁柱连接节点，之后梁柱连接节点将大部分荷载传递至下塔柱。为了清楚描述八边形塔柱各个板件承担荷载情况，计算了桥塔各个板件的轴力，得到各个板件承担轴力比例如表2所示。

图4 塔柱板件编号示意图Fig．4 Pylon plate lable

从表2可以看出，梁柱节点上塔柱与下塔柱的各个板件承担竖向压力比例基本相同。在弯矩作用下，塔柱内侧的板件承担较多的竖向压力，板件UW(DW)-1、7、8三块板件的竖向压力为总竖向压力的60%～65%。UW-8和DW-8承担的竖向压力最多，分别承受28．11%和25．80%的竖向压力。

表2 塔柱板件轴力分配比例Table 2 Axial force sharing ratios for pylon plates

4．2 横梁受力分析

图5为节点横梁的剪应力分布图。在空间钢框架结构中，横梁主要起到传递荷载的作用。从图5(a)和图5(b)可以看出，横梁顶底板的剪应力在弯折处出现极值，顶板最大剪应力约为25 MPa，底板最大剪应力约为26．6 MPa;而板中其他部分的剪应力分布较为均匀。从图5(c)和图5(d)可以看出，横梁腹板的剪应力在与顶底板相交处出现极值，内侧腹板最大剪应力约为7．5 MPa，外侧腹板最大剪应力约为35 MPa;远离节点处的横梁腹板剪应力较为均匀。从图中的剪应力分布情况来看，横梁在梁柱连接节点附近主要受到横向弯曲并伴有扭转作用，这与一般的梁柱节点受力不同。

图5 横梁剪应力分布图(单位:kPa)Fig．5 Beam shear stress contour(Unit:kPa)

4．3 节点受力分析

通过有限元模型计算分析，得到梁柱连接节点的详细受力情况。这里选取有斜拉索锚固塔柱的梁柱连接节点进行板件受力特性分析。

图6为梁柱连接节点Mises应力分布图。从图中可以看出，梁柱连接节点内侧的应力明显高于节点外侧，节点内侧应力分布不均匀。梁柱连接节点在塔柱与横梁相交处出现应力集中，最大Mises应力约为210 MPa，其他部位板件的Mises应力大部分在140 MPa以下。梁柱节点内侧应力扩散很快，上下塔柱Mises应力大部分在90 MPa以下。横梁的Mises应力外侧高于内侧，但总体水平不高，约50 MPa。

图6 梁柱连接节点Mises应力分布图(单位:kPa)Fig．6 Beam-column joint Mises stress contour(Unit:kPa)

计算分析表明，梁柱连接节点板件的Mises应力在板件相交处较大，但均未超过材料的屈服应力，结构安全。

为了进一步地分析梁柱连接节点壁板的受力情况，选取图 7 所示的 A—A、A'—A'、B—B、C—C和C'—C'五个断面，分析壁板在荷载作用下的竖向应力分布。

图7 梁柱节点示意图Fig．7 Beam-column joint

从图8中可以看出，壁板竖向正应力在节点与塔柱相交面附近(A—A、A'—A'、C—C 和C'—C')分布不均匀，在节点内部(B—B)分布较为均匀。

从图8(a)和图8(e)中可以看出，A—A和C—C位置处壁板在距离形心约为－1 m和－2 m距离处出现应力的突然变化，这是由于壁板弯折出现刚度突变而导致的。从图8(b)和图8(d)中可以看出，由于横梁顶板加劲肋对于节点壁板的约束作用，在A'—A'和C'—C'位置处壁板与横梁相交部分出现复杂的波动变化，其波动变化较大，个别位置应力已经超过了梁柱连接节点下翼缘应力。从图8(c)可以看出，在节点中央(B—B)，壁板应力变化均匀，但在距离形心1 m处由于壁板弯折而导致应力曲线的斜率发生变化，而在形心位置以下部分板件由于横梁的约束作用而使得应力曲线的斜率基本保持恒定。

通过对比杆系模型和板壳模型在各个断面处的计算结果可以发现(见表3)，除了B—B断面外，其他位置处两种计算模型的结果偏差较大，最大偏差为20．11%。而B—B断面处两种计算模型的结果吻合较好，最大压应力偏差为7．36%，最大拉应力偏差为0．53%。

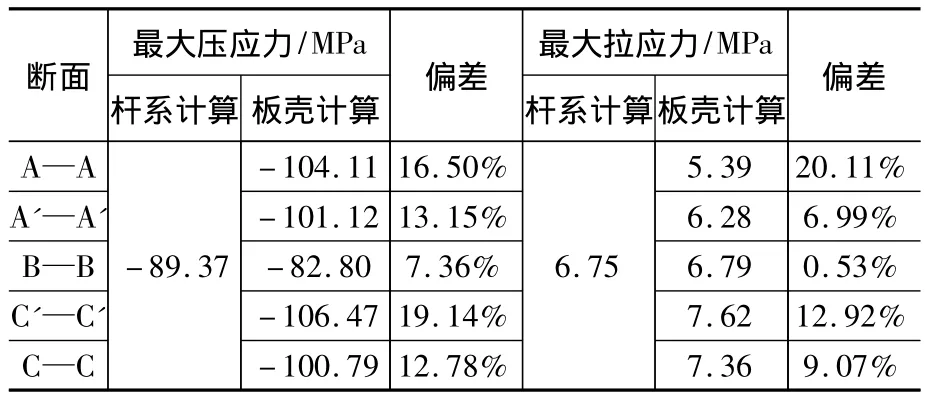
表3 梁柱连接节点壁板竖向应力极值Table 3 The maximum and minimum stress of wall panels in the beam-pylon joint

5 结论

图8 梁柱连接节点壁板竖向正应力Fig．8 Normal stress of wall panels in the beam-column joint

本文以宜兴范蠡大桥为背景，通过建立空间杆系和板壳有限元程序，对梁柱连接节点板件应力状态等方面进行研究分析。分析表明:

(1)梁柱连接节点上下塔柱各板件承担荷载比例基本相同，塔柱内侧板件承担了60%～65%的轴力。横梁各个板件剪应力较小，在梁柱连接节点附近受到横向弯曲和扭转作用。

(2)梁柱连接节点各板件受力复杂，应力变化较大。各板件Mises应力在210 MPa以下，高应力区域范围较小，应力扩散较快，梁柱连接节点承载能力满足要求。

(3)采用杆系有限元和板壳有限元计算得到梁柱连接节点处板件应力相差较大，最大偏差约为20%，对该连接节点应采用板壳有限元方法分析。

［1］ 陆春阳，吴冲，曾明根，等．火炬桥异型钢索塔局部应力分析［J］．计算机辅助工程，2007，16(4):27-30．Lu Chunyang，Wu Chong，Zeng Minggen，et al．Local stress analysis on abnormal steel pylon of torch bridge［J］．Computer Aided Engineering，2007，16(4):27-30．(in Chinese)

［2］ 吴万忠，庄冬利，肖汝诚．某大跨异型独塔斜拉桥关键节点空间应力分析［J］．石家庄铁道学院学报(自然科学版)，2008，21(3):24-28．Wu Wanzhong，Zhuang Dongli，Xiao Rucheng．Spatial stress analysis for key joints of Long span specialshaped cable-stayed bridge with single pylon［J］．Journal of Shijiazhuang Railway Institute(Natural Science Edition)，2008，21(3):24-28．(in Chinese)

［3］ 黄珏，肖建庄，葛亚杰，等．异形柱框架节点受力性能研究进展与评述［J］．结构工程师，2002，(1):52-57．Huang Jue，Xiao Jianzhuang，Ge Yajie，et al．Investigation on frame joint with special-shaped columns［J］．Structural Engineers，2002，(1):52-57．(in Chinese)

［4］ 胡宗波．钢结构箱形柱与梁异型节点设计方法研究［J］．工程力学，2012，29(11):191-196+235．Hu Zongbo．Study on design method for irregular joints between steel box columns and beams［J］．Engineering Mechanics，2012，29(11):191-196+235．(in Chinese)

［5］ 童根树，王继涛，张磊．箱形柱与工字梁连接节点翘曲变形的传递分析［J］．工程力学，2011，28(6):96-102，109．Tong Genshu，Wang Jitao， Zhang Lei． Warping transfer through joints of RHS column and I-beam［J］．Engineering Mechanics，2011，28(6):96-102，109．(in Chinese)

［6］ 刘洪波，谢礼立，邵永松．钢结构箱形柱与工字梁刚性节点有限元分析［J］．哈尔滨工业大学学报，2007，39(8):1211-1215．Liu Hongbo，Xie Lili，Shao Yongsong．Finite element analyses of the rigid connections with steel box columns and I section beams［J］．Journal of Harbin Institute of Technology，2007，39(8):1211-1215．(in Chinese)

［7］ Davor S，Darko D，Boris A．Reliability of the bending resistance of welded beam-to-column joints［J］．Journal of Constructional Steel Research，2008，64(4):388-399．

［8］ Mishima Y，Ono K，Miyoshi T，et al．Effect of shear panels on elasto-plastic behavior of beam-to-column connections of steel rigid frame piers［J］．Procedia Engineering，2011，14:100-107．