地铁引起建筑结构振动及室内辐射噪声的数值分析

肖永武 汪 洁 唐和生 赵伟屹

(1．中铁电气化局京沪高铁维管公司，北京100039;2．上海南汇汇集建设投资有限公司，上海201300;3．同济大学结构工程与防灾研究所，上海200092;4．中冶焦耐工程技术有限公司，大连116085)

1 引言

伴随着轨道交通在我国各大城市的迅猛发展，其引发的各类环境问题也日益受到人们关注。在城市人口密集区，特别是老式住宅区，地铁沿线的居民直接受到振动及建筑物内二次辐射噪声的影响［1］。人们对二次辐射噪声的敏感程度远远高于空气噪声，其影响与危害日益受到公众重视，上海、北京等地区的地铁交通已多次收到沿线居民关于室内噪声问题的投诉［2］。

建筑物内二次噪声与地铁列车振动传播的诸多影响因素有关，而地铁环境振动又是横波、纵波、表面波合成的复杂波动现象，其振动机理、传播形态受各种复杂因素影响。研究表明:影响地铁列车振动传播的影响因素包括地铁车辆条件、轨道线路状况、地基地质条件、建筑物距地铁线路距离、建筑物特性等［3］，其中影响建筑物内二次结构噪声的建筑物特性与建筑物整体质量刚度、地板质量刚度、质量分布、材料阻尼、地板和墙壁尺寸、建筑物内表面吸声条件、二次辐射噪声效率等参数有关，这使二次噪声的预测比空气噪声复杂得多［4］。

当前，建筑物二次辐射噪声问题的研究多是以实测为主［5］，缺乏有效的数值模型分析。同时，由于影响二次辐射噪声声场分布的因素较多，所以同时需要实测与数值模拟来对建筑物内二次辐射噪声进行评价与分析。

本文基于现场实测结果，以有限元软件和声学边界元软件为研究平台，采用有限单元法分析地铁引起建筑物结构的振动响应，以此作为房屋室内声场的边界条件，分析室内二次结构噪声响应以及声场分布特性。根据已有文献的建议［6，7］，对 16 ～250 Hz频率内的噪声特性进行频域分析，并与实测结果进行了比较。

2 数值分析模型

建筑结构受到激振产生振动，结构噪声则主要由结构振动控制。为了取得楼板与墙面在地铁激励下的振动响应，首先对测试建筑进行有限元分析。

2．1 有限元模型

测试建筑为上海某条地铁线路沿线房屋，该建筑物位于轨道弯道附近，弯道半径400 m，测点处地铁隧道埋深为11．65 m。测试建筑物类型为6层砌体结构，为典型上世纪居民楼，该建筑物共有4个单元，长 43．95 m，宽 13．088 m，建筑标准层平面图如图1所示。

图1 建筑平面图(单位:mm)Fig．1 Architectural plan of a building(Unit:mm)

图2 建筑物网格模型Fig．2 Mesh model of the bulding

在ANSYS软件中建立建筑物有限元模型(图2)，梁柱采用 BEAM4单元，楼板和墙体采用SHELL63单元。考虑到建筑物上部结构与基础固接，故有限元模型底部采用三向约束。利用现场实测地铁运行引起的地面振动加速度时程数据［8］，建立刚性地基结构模型，以有限单元法分析地铁运行引起建筑物结构的振动响应。为了研究房屋室内声场的边界条件，主要对房屋各层的楼面与墙面振动响应进行时程与频谱分析。分析中主要计算参数如表1所示。

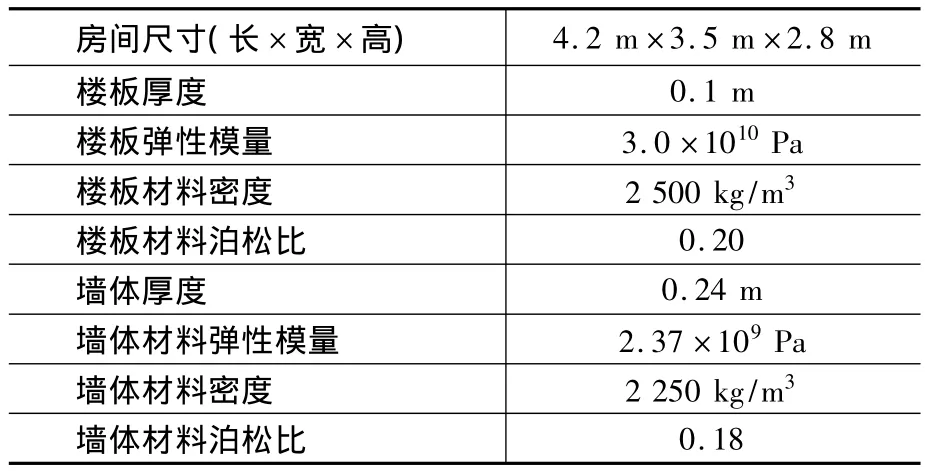
表1 ANSYS模型分析主要计算参数Table 1 Parameters of the ANSYS model

实测建筑物地面三向加速度时程曲线如图3所示。采用一致输入，分析时不考虑土与结构相互作用［9］;计算采用直接积分法，时间步长取0．002 s;阻尼为瑞利阻尼。

图3 3个方向的地面加速度Fig．3 Ground acceleration in three dimensions

2．2 声场边界元模型

有限元计算得到建筑物楼面与墙面的振动响应，以此作为边界条件，建立建筑物室内声场边界元数值模型，计算分析室内二次结构噪声响应以及声场分布特性。

2．2．1 Virtual Lab 声学模型

在Virtual Lab声学模块中导入声场边界元模型，为了满足单元尺寸小于计算频率最短波长1/6的划分条件，声场边界元的最大尺寸为20 cm。由于计算封闭声场分布，故计算方法可采用直接边界元法。综合考虑现场建筑环境，材料吸声特性及实测频段，材料吸声系数统一设置为0，以最不利全反射情况研究声场特性［10］。声场计算主要参数见表2。

2．2．2 声场频率域模态

计算得声场声频率如表3所示。声模态信息如图4所示。

表2 声场主要计算参数Table 2 Parameters of the sound field

表3 室内声模态频率Table 3 Modal frequency of the sound field

图4 室内声场模态图Fig．4 Mode of the sound field

3 计算结果分析

由于受现场测试条件的限制，仅得到一、二层有效的现场测试数据。在此基础上，通过数值模拟结果与实测结果的比较，来说明模型的合理性。

图5与图6分别给出一、二层楼板板中处振动加速度时程比较曲线。

图5 一楼楼板Fig．5 The first floor slab vibration

图6 二楼楼板Fig．6 The second floor slab vibration

比较分析表明，数值结果与实测数据在幅值上比较一致。二楼振动幅值比一楼大0．005～0．01 m/s2。

图7与图8给出室内振动的1/3倍频程曲线。

对比可知:1/3倍频程数值结果与实测结果基本一致。具体而言，数值结果在1～12．5 Hz范围振级偏小，在16～200 Hz范围与实测结果基本吻合。这主要是因为在有限元模型分析中，振动输入低频成分较少;同时，在实测中，低频段部分受到干扰较大，实测结果本身包括干扰成分，使得结果偏大。

表4为一、二层数值模拟与实测结果的VLzmax比较。

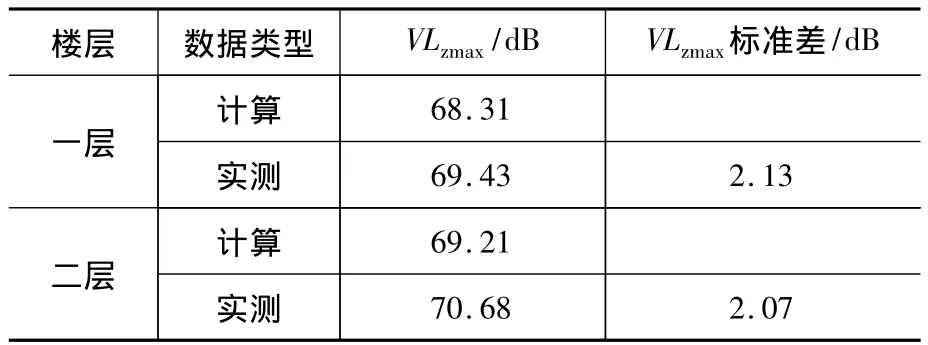
表4 数值模拟与实测的VLzmax比较Table 4 Comparation between the numerical simulation and the actual VLzmax

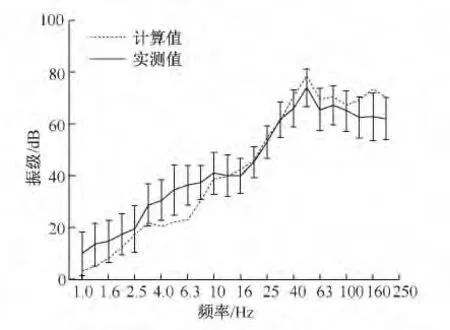
图7 一楼数值结果与实测结果比较Fig．7 Comparation between simulations and actual measurements of the first floor

图8 二楼数值结果与实测结果比较Fig．8 Comparation between simulations and actual measurements of the second floor

可见，在一、二层，数值计算振级结果与实测基本吻合。图9给出带实测结果的1～5层的模拟结果。可知二楼的结果最大且略高于一楼的振动，其他楼层的结果均小于一楼的振动且呈现随楼层增加而衰减的趋势，这个结果与文献［11］的结果相似。

数值模拟显示出合理的衰减趋势，同时结合前述，说明该计算方法在一定精度下可以用于建筑物楼板振级的预测分析。

图9 1到5层VLzmax计算结果Fig．9 Numerical simulation of VLzmaxfrom the 1st floor to the 5th floor

楼板、墙面速度激励下，距地面1．2 m声场场点采用直接边界元计算所得16～250 Hz范围内1/3倍频程中心频率点的声场场点声压分布如图10所示。

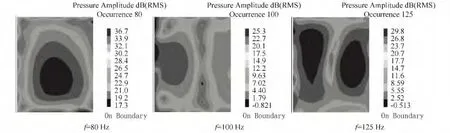
图10 声场场点声压级云图Fig．10 Nephogram of SPL of the sound field

可见低频区域房间边缘声压较强，并随频率升高向房间中间区域转移。图11给出一、二层数值模拟与实测声压级1/3倍频程曲线。

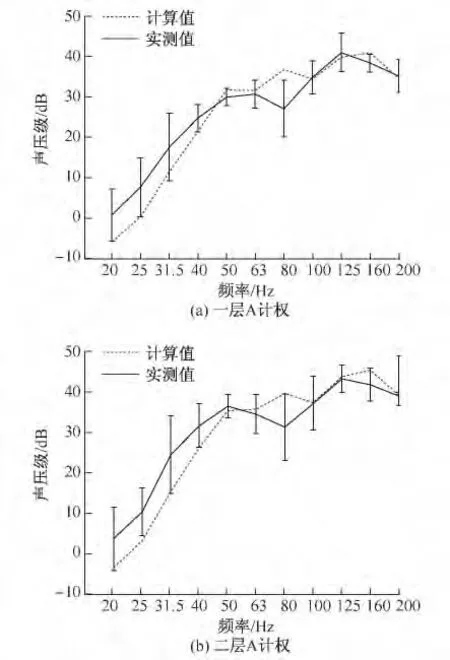
图11 一、二楼数值模拟与实测声压级1/3倍频程Fig．11 Comparation between numerical simulations and actual one-third octave of two floors

由图11可知，数值模拟声压1/3倍频程与实测结果基本一致。在20～40 Hz，数值模拟结果偏小;在50～200 Hz，二者基本吻合。这主要因为在低频范围，振动数值模拟结果低频响应较小;同时，由于背景噪声主要集中在低频范围内，使得噪声实测中，低频段的声压级测试结果较真实值偏大。

对该建筑物的其他楼层数值模拟与实测声压级1/3倍频程曲线如图12。由图可知:以二楼为准，室内声压数值结果随着楼层的增加而减小;中心频率点为160 Hz的声压级随楼层变化较大，基本相邻楼层相差5 dB。

图12 2～5楼室内测点声压级1/3倍频程曲线Fig．12 Numerical simulation of the one-third octave from the 2nd floor to the 5th floor

表5为数值模拟与实测噪声在20～200 Hz的等效连续A声级，图13为所有楼层LAeq计算结果。

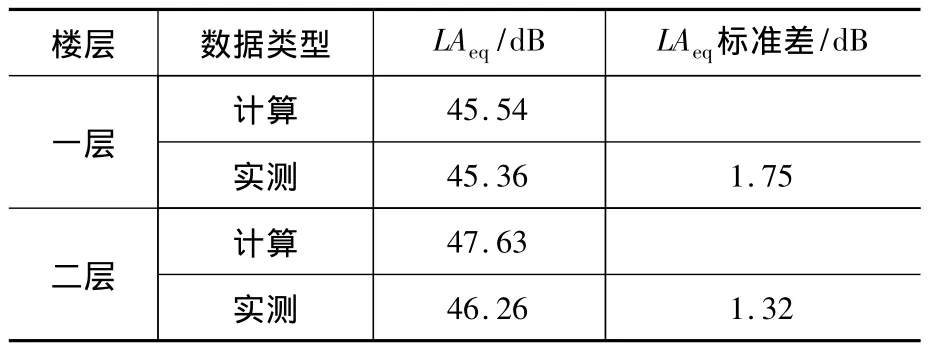
表5 数值模拟与实测等效连续A声级Table 5 Comparation of simulation and actual equivalent A aound level

由表5及图13可知:数值计算的等效计权A声级与实测结果基本吻合;二楼比一楼大，且数值计算结果基本在实测结果上下小幅合理波动。计算模拟同样显示出合理的衰减趋势，说明该计算方法在一定精度下可以用于建筑物二次辐射噪声室内声压级的预测分析。

图13 1到5层等效连续A声级Fig．13 Simulation of the equivalent A sound level from the 1st floor to 5th floor

4 结论

本文利用结构有限元模型计算了建筑物室内楼面与墙面的振动，数值结果的比较分析得到如下结论:

(1)不同楼层，二楼室内振级最大，其上楼层室内振级随楼层的增加而降低;

(2)一、二层的数值计算结果与实测基本吻合，增加了数值模型的可信度，使得较高楼层的计算结果可以作为评判的参考值，表明该方法能在一定程度上为建筑物室内振动提供预测与分析。

声场边界元的数值模拟结果表明:

(1)不同楼层，二楼室内声压级最大，其余楼层室内声压级随着楼层增加呈现下降趋势，这与振动结果相符合;

(2)低频段，实测结果由于背景噪声的影响略大于数值模拟结果，但变化趋势一致，在50～200 Hz，二者基本吻合，可见使用该方法预测分析建筑物室内辐射噪声切实可行［12］。

［1］ 洪俊清，刘伟庆．地铁对周边建筑物振动影响分析［J］．振动与冲击，2006，25(4):142-145，183．Hong Junqing，Liu Weiqing．Analysis on effects induced by subway train on surrounding building vibration［J］．Journal of Vibration and Shock，2006 25(4):142-145，183．(in Chinese)

［2］ 王毅．北京地下铁道振动对环境影响的调查与研究［J］．地铁与轻轨，1993，(2):21-25．Wang Yi．Investigation and study of the beijing subway trains vibration impact on the environment［J］．Urban Rapid Rail Transit，1993，(2):21-25．(in Chinese)

［3］ 楼梦麟，李守继．地铁引起建筑物振动评价研究［J］．振动与冲击，2007，26(8):68-71．Lou Menling，Li Shouji．Evaluation research of building vibrations induced by subway running train［J］．Journal of Vibration and Shock，2007，26(8):68-71．(in Chinese)

［4］ 马筠．地铁列车振动对临近建筑物内结构噪声的影响［J］．噪声与振动控制，2005，(S):93-98．Ma Jun．The effects of structure-borne sound by subway trains vibration on surrounding buildings［J］．Noise and Vibration Control，2005，(S):93-98．(in Chinese)

［5］ 王毅，徐辉．地铁车辆段平台居住小区震动与噪声污染控制［J］．中国环境监测，1999，15(06):43-45．Wang Yi，Xu Hui．A brief talk on the pollution controlling of vibration and noise of the community builded on the platform of subway traffic［J］．Environmental Monitoring in China，1999，15(06):43-45．(in Chinese)

［6］ Kurzweil L G．Ground-borne noise and vibration from underground rail systems［J］．Journal of Sound and Vibration，1979，66(3):363-370．

［7］ Dawn T M，Stanworth C G．Ground vibrations from passing trains［J］．Sound and Vibration，1979，66(3):355-362．

［8］ 上海市质量技术监督局．DB31/T 470—2009城市轨道交通(地下段)列车运行引起的住宅室内振动与结构噪声限值及测量方法［S］．北京:中国建筑工业出版社，2009．Shanghai Bureau of Quality and Technical Superivsion．DB31/T 470—2009 Limits and measurements methods for vibration and ground-borne noise in dwells caused by the moving vehicles of urban rail transit(underground railway)［S］．Beijing:China Architecture and Building Press，2009．(in Chinese)

［9］ François S，Pyl L，Masoumi H R，et al．The influence of dynamic soil-structure interaction on traffic induced vibrations in buildings［J］．Soil Dynamics and Earthquake Engineering，2007，27(7):655-674．

［10］ 冯青松，雷晓燕，伍明辉．地铁运行列车引起建筑物低频振动的数值分析［J］．铁道科学与工程学报，2007，4(5):68-72．Feng Qingsong，Lei Xiaoyan，Wu Minghui．Numerical analysis of building underlow-frequency vibrations induced by subway running train［J］．Journal of Railway Science and Engineering，2007，4(5):68-72．(in Chinese)

［11］ 夏禾．交通环境振动工程［M］．北京:科学出版社，2010．Xia He．Traffic induced environmental vibrations and controls［M］．Beijing:Science Press，2010．(in Chinese)

［12］ 中华人民共和国环境保护部．HJ 453—2008环境影响评价技术导则城市轨道交通［S］．北京:中国环境科学出版社，2009．Ministory of Environmental Protecting of the People's Republic of China．HJ 453—2008 Technical guidelines for environment impact assessment of urban rail transit［S］．Beijing:Environmental Science Press，2009．(in Chinese)