关于圈对完全图的多色Ramsey数
2014-03-20刘大瑾白路锋
刘大瑾, 白路锋
(南京理工大学泰州科技学院 江苏泰州225300)
0 符号说明
本文中的图都是指简单图.设图G=(V,E),V为顶点集,E为边集.如果V'⊆V(G),则以V'为顶点集,以2个端点均在V'的边集组成的图,称为图G的点导出子图,记为G[V'].用Γ(u)表示u的邻域,即u的所有邻点构成的集合,由Γ(u)产生的点诱导子图记为G'[Γ(u)].如果E'⊆E(G),则以E'为边集,以E'中边的所有端点为顶点集组成的图,称为图G的边导出子图,记为G[E'].分别用G1,G2,…,Gm表示图,(k+1)色Ramsey数rk+1(C2m,…,C2m,Kn)是指满足如下条件的正整数N:当用(k+1)色c1,c2,…,ck+1给完全图KN边着色时,总存在某个 j∈{1,2,…,k},使得 C2m⊂G'[Ecj]或者 Kn⊂G'[Ec(k+1)],这里 Ecj表示用颜色 cj染色的边集.α(G)表示图G的独立数.f(n)、g(n)分别表示关于n的函数,f(n)≤(1+o(1))g(n)是指对于任意ε>0,总存在一个正整数N,使得n>N时有f(n)≤(1+ε)g(n).定理证明中要用到高斯超几何函数[1]

当x∈(0,+∞)时,fm(x)是正的单调减少的凸函数,且fm(x)>(log(x/m)-1)/x,x>m.
1 rk+1(C2m,…,C2m,Kn)上界的证明
文献[2]研究了 r(C2m,Kn),文献[3]研究了 rk+1(C4,…,C4,Kn),本文研究了更一般的情况 rk+1(C2m,…,C2m,Kn).
引理1[4]设图G顶点数为N,平均度为d.设Gv是v的邻点导出子图,平均度不超过a,则

定理1 当n足够大时,rk+
证明 设 N=rk+1(C2m,…,C2m,Kn)-1,用 c1,c2,…,ck+1种颜色对 Kn边着色,使得 G'[Ec1],G'[Ec2],…,G'[Eck]中分别不含有 C2m.设 G*=G'[Ec1]∪G'[Ec2]∪…∪G'[Eck],由 N 的设法可知 n-1 > α(G*).下面推导出G*的平均度以及G'[Γ(v)]的平均度.
图F的Turán数是指N个顶点的图中不含有图F的最大边数,用ex(N,F)来表示.在文献[3]中有ex(N,C2m)≤q1m,因为 G'[Ecj]中不含有 C2m,j=1,2,…,m,从而 G'[Ecj]的平均度最多为 2q1m,故有d(G*)≤2q1m
设Ni为G*中度为i的点的个数,则对于∀ε>0有

设H为G*中度小于(1+ε)d的点产生的诱导子图,由(2)可知H的阶至少为N-N/(1+ε)=εN/(1+ε)。取ε=1,则H的阶至少为N/2,H的最大度小于2d(由H的设法可知).设Δ(H)为H的最大度,则Δ(H这里 q2=q2(m,k).
由于H是G*的子图,故H不含有c1,c2,…,ck颜色的C2m.对于H的任意一点u,设H'[Γ(u)]为u的邻域在H中的诱导子图,则H'[Γ(u)]也不含有c1,c2,…,ck颜色的C2m.用上述同样的方法可得H'[Γ(u)]的最大度 Δ(H'[Γ(u)])≤q2
由于H是G*的诱导子图,故H的独立数不超过G*,即n-1≥α(G*)≥α(H).H的平均度记为d(H),显然d(H)≤Δ(H),由(1)及高斯超几何函数的性质可得
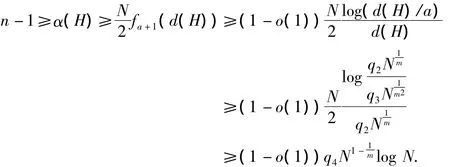

[1] Li Yusheng,Rousseau C C,Zang Wenan.Asymptotic upper bounds for Ramsey functions[J].Graph Combinatorics,2001,17(1):123-128.
[2] Yair C,Li Yusheng,Rousseau C C,et al.Asymptotic bounds for some bipartite graph:complete graph Ramsey numbers[J].Discrete Mathmatics,2000,220(1/2/3):51-56.
[3] Alon N,Rödl V.Sharp bounds for some multicolor Ramsey numbers[J].Combinatorica,2005,25(2):125-141.
[4] Li Yusheng,Rousseau C C.On book-complete graph Ramsey numbers[J].J Combin Theory:Ser B,1996,68(1):36-44.
