一类渐近线性椭圆方程非平凡解的存在性

刘春晗， 王建国

(齐鲁师范学院数学系 山东济南250013)

献［2］知，H20(Ω)⊂ H(Ω)⊂ W1，p0(Ω)，同时记

对于任意的

0 引言

文献［1］在新的Hilbert空间H中研究了特征值问题

证明了问题(1)有解，其中H是将H20(Ω)空间按下列范数的完备化空间，H为按内积〈dx的Hilbert空间．如果1≤p＜2，由文

献［2］知，H20(Ω)⊂ H(Ω)⊂ W1，p0(Ω)，同时记

首先在空间H中讨论(1)的特征值问题．

第一特征值定义为λ1

第二特征值定义为λ2

类似地，可以定义第n个特征值λn，?

其相应的特征函数记作φn．

存在非平凡解．

本文利用山路引理，在f满足无穷远处共振的情况下研究了非线性椭圆型方程(2)的存在性问题．

对于任意的

下面给出一些假设条件:

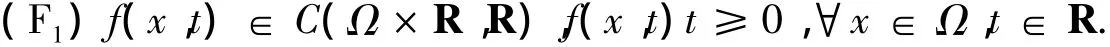
(F0)对某一个正数C及所有的N≥5．，对 a．e．x∈ Ω 一致，其中 A ＜ λ1＜ B，B= λk，k≥2，且 λk是特征值问题(1)对应的特征值，或者B=+∞．

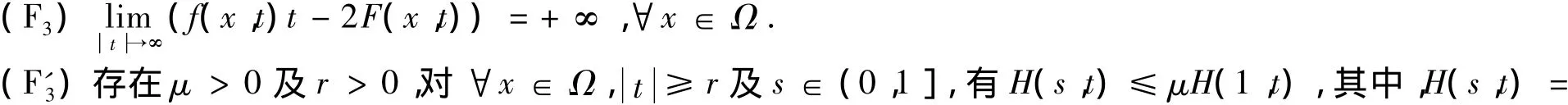
定义1 设Φ∈C1(E，R)，称Φ对于每一个c∈R满足(C)c条件，若任意满足

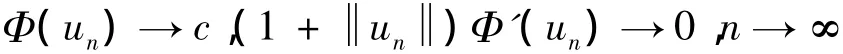
的数列{un}都有收敛子列，称Φ满足(C)条件，如果Φ对于每一个c∈R满足(C)c条件．

引理1［3］Hilbert空间H紧嵌入到L2(Ω)空间中．

引理2 假设f(x，t)满足(F0)、(F2)、(F3)，且B= λk，则泛函 Φ 满足(C)条件．

证明 首先证明{un}是有界的．假设un满足

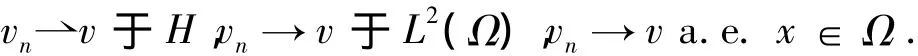
若v(x)≠0，由(F2)可得λk．在 L2(Ω)中，vn→ v，则有

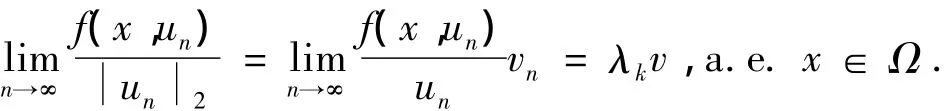
由(F3)可知根据 Fatou 引理可得．因为

另一方面，可以得到

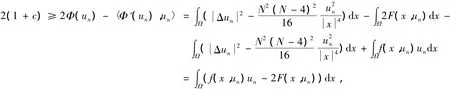
矛盾，因此{un}是有界的．于是{un}在H中有弱收敛的子列，仍记为{un}，记弱极限为u．由引理1，可以看出在L2(Ω)中 un→u．再由(1+ un)Φ'(un)→0，有

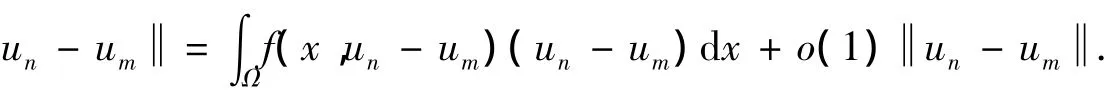
引理3 假设 f(x，t)满足(F0)、(F2)、(F'3)，如果设{un}⊂ H，〈Φ'(un)，un〉→ 0，并且{tn}⊂ R，tn＞ 0，tn→0．令 wn=tnun，则当 n充分大时，有 Φ(wn)≤ μΦ(un)+o(1)．

证明 当n充分大时，有t2n〈Φ'(un)，un〉→ 0，从而

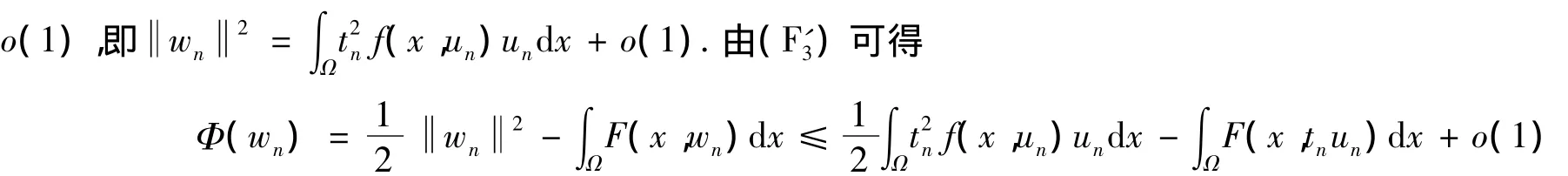
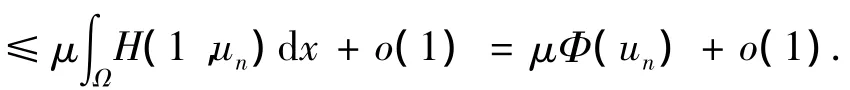
引理4 假设 f(x，t)满足(F0)、(F2)、(F'3)，且B=+∞，则泛函Φ满足(C)条件．

证明 假设un满足(1+ un)Φ'(un)→0，Φ(un)→c．设 un→+∞，令有界．因此可以假设2

下面考虑2种情况:1)v≠0;2)v=0．

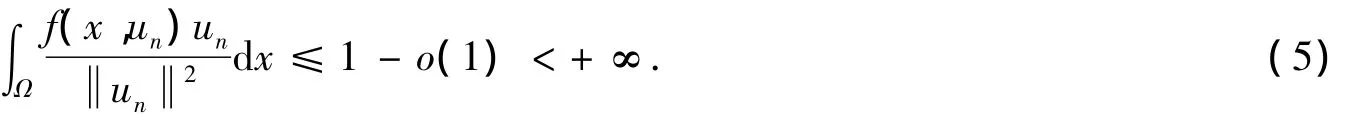
n设∑ ={x∈Ω:v(x)≠0}，则，由条件(F2)可得，对于任意的x∈∑，有

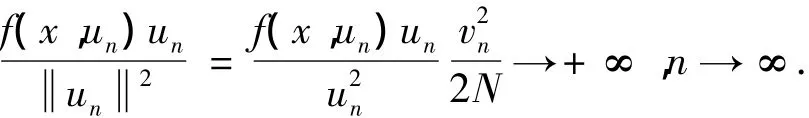
另一方面，由条件(F1)、(F2)可得，存在η ＞ － ∞，对于(x，t)∈Ω ×R，有．注意到当n→∞时则存在 T＞ －∞，使得

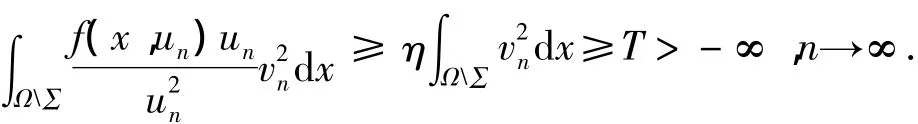
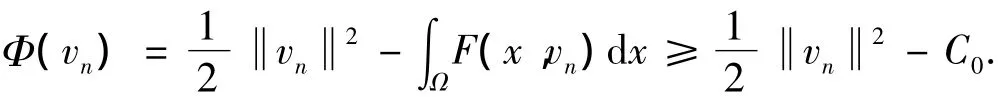
由引理3可知

综上，{un}是有界的，类似于引理2即证得Φ满足(C)条件．

定理1 (山路引理)假设φ∈C1(E，R)满足max{φ(0)，φ(1)}≤α ＜β≤||iu|n|=fρφ(u)，对某一个 α ＜β，ρ ＞ 0且u1∈E， u1＞ ρ．令Γ ={γ∈C(［0，1］，E):γ(0)=0，γ(1)=u1}．且c=inf maxφ(γ(τ))．

γ∈Γτ∈［0，1］则c≥β＞0且存在序列{un}⊂E，使得φ(un)→c，(1+ un)φ'(un)→0，n→∞，而且，如果φ满足(C)c条件，则c是φ的临界点．

1 主要结果

定理2 如果f(x，t)满足(F0)～(F3)且B=λk，则方程(2)至少存在一个非平凡解．

由(F2)可得，对∀ε ＞0，存在C2＞0，使得 F(x，u)≤A+ε)u2+C2up+1．取 ε ＞0充分小，使得A+ε ＜ λ1，由Poincaré不等式和Sobolev不等式，有

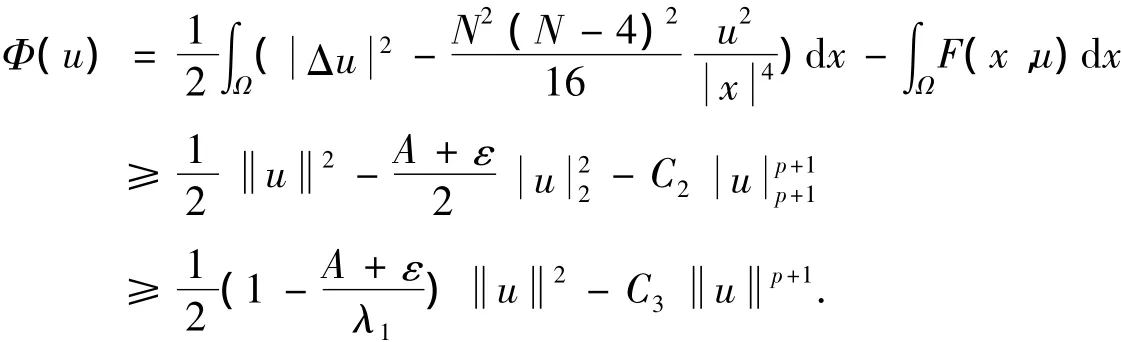
另一方面，B= λk，由(F2)可知，对于 ∀ε ＞ 0，存在C4＞ 0，使得F(x，u)≥(λk－ ε)u2－ C4．取ε＞0充分小，使得λk－ε＞λ1，有

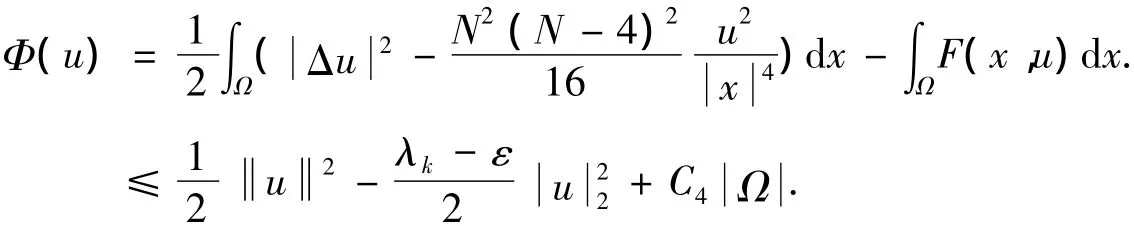
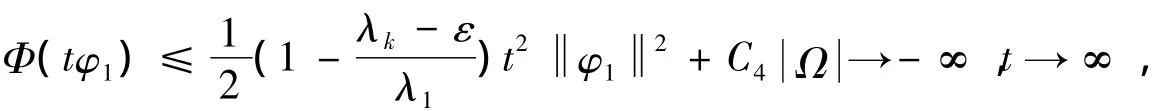
则存在e∈H， e ＞ r，使得Φ(e)≤0．

所以Φ满足定理1的所有条件，由定理1可得，方程(2)至少存在一个非平凡解．

定理3 如果f(x，t)满足(F0)～(F2)和(F'3)，且B=+∞，则方程(2)至少存在一个非平凡解．

证明 由引理4可得，Φ(u)满足(C)条件．下面证明Φ(u)满足山路引理的其他条件．

由定理2的证明可得存在 u =r＞0，使得Φ∂Br≥α ＞ 0，其中Br={u∈H:u ≤r}．

因为B=+∞，由(F2)可知，对于任意的M ＞0，存在C5＞0，使得F(x，u)≥Mu2－C5，x∈Ω．

因此，有 F(x，tφ1)≥ Mt2φ12－C5，x∈ Ω ．这里 φ1是相对于特征值 λ1的特征函数，两边同除以t2，有．进而，可得

设u=tφ1，这里φ1是相对于特征值λ1的特征函数，φ1=1，有

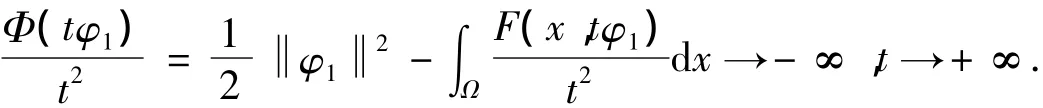
取t0充分大，且e=t0φ1，则Φ(e)＜0．因此Φ满足定理1的所有条件，故方程(2)至少存在一个非平凡解．

注1 在研究超线性问题时，许多文献都要求f(x，t)/t关于t是单调增加的或者f(x，t)满足条件:存在θ≥ 1，对(x，t)∈ Ω × R，s∈［0，1］，有 G(x，st)≤ θG(x，t)，其中 G(x，t)=f(x，t)t－ 2F(x，t)．容易看出这里的(F'3)是比前面的2个条件都要弱，因此我们推广了一些已知的结果．

［1］ 伍芸，姚仰新，柯敏．含Hardy位势的双调和方程特征值问题［J］．山东大学学报:理学版，2008，43(9):81－84．

［2］ Adimurthi Grossi M，Santra S．Optimal Hardy-Rellich inequalities，maximun principle and related eigenvalue problem［J］．J Funct Anal，2006，240(1):36 －83．

［3］ 伍芸，何少通，沈尧天．一类渐近线性双调和方程非平凡解的存在性［J］．数学学报，2011，54(1):9－14．

［4］ Liu Xiangqing，Huang Yisheng．On sign-changing solution for a fouth-order asymptotically linear elliptic problem［J］．Nonlinear Analysis，2010，72:2271 －2276．

［5］ 陈自高，谷留新．含Hardy位势的超线性p-Laplace方程的无穷多解［J］．郑州大学学报:理学版，2012，44(1):11－14．

［6］ 裴瑞昌．p拉普拉斯Dirichlet问题的平凡解［J］．数学物理学报，2013，33A(1):165－173．

［7］ Liu Jiaquan，Su Jiabao．Remark on multiple nontrivial solutions for quasi-linear resonant problem［J］．J Math Anal Appl，2001，258:209－222．

［8］ 伍芸，韩亚蝶．一类临界位势非线性椭圆型方程非平凡解的存在性［J］．山东大学学报:理学版，2012，47(10):1－5．

［9］ Pei Ruichang．Multiple solutions for biharmonic equations with asymptotically linear nonlinearities［J］．Boundary value problem，2010(5):1－11．

［10］丁凌，周良金，张丹丹．在混合边界条件下临界指数椭圆方程的解［J］．四川师范大学学报:自然科学版，2011，34(4):521－527．

［11］祁瑞改，杨国英．用山路引理证明拟线性方程组正解的存在性［J］．郑州大学学报:理学版，2010，42(3):19－22．