高阶分数阶微分方程边值问题正解的存在性

刘东利， 杨 军， 崔更新

(1.燕山大学理学院 河北秦皇岛066004;2.河北省数学研究所 河北石家庄050000;3.北京理工大学数学学院 北京100081)

0 引言

分数阶微分方程是整数阶微分方程的推广，很多自然界和社会中的现象都可以采用分数阶微分方程作为它们的数学模型［1-4］，使大多数用整数阶导数无法解释的问题得以解决，包括流体力学、流变学、生物学图像与信息处理、生物种群的繁衍以及目前较为新颖的系统辨识［5］等.近些年来，人们更深入研究了分数阶微分方程的各种边值问题，并取得了重要成果［6-11］.

文献［12］研究了分数阶微分方程边值问题

正解的存在性，其中0≤β≤1，Dα0+是标准的Rieman-Liouville分数阶导数．在此基础上，本文研究了一类非线性分数阶高阶微分方程边值问题

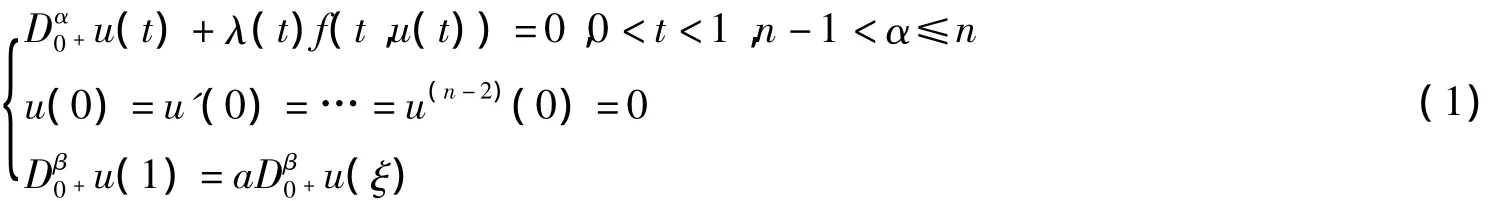
正解的存在性，其中0≤β≤1，0≤a≤1，ξ∈(0，1)，ρ=aξα－β－1＜1，Dα0+是标准的Rieman-Liouville分数阶导数，并且函数 f:［0，1］×［0，∞)→［0，∞)连续，函数 λ:［0，1］→［0，∞)连续且

1 预备知识

定义1 函数f:(0，+∞)→R的α＞0阶Riemann-Liouville分数阶积分定义为

定义2 连续函数f:(0，+∞)→R的α＞0阶Riemann-Liouville分数阶导数定义为

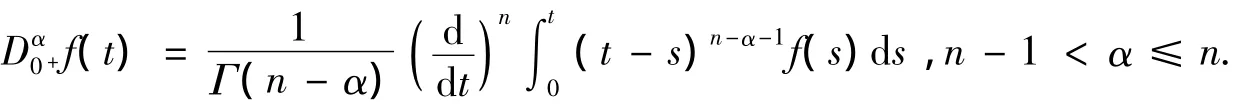
引理2 如果g(t)∈L(0，1)，α，β为两个正数，且α ＞1≥β≥0，则

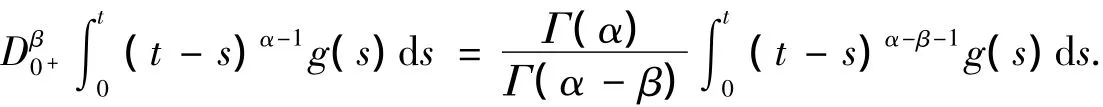
2 主要结果和证明

引理3 假设g(t)∈L(0，1)，考虑线性分数阶高阶微分方程边值问题

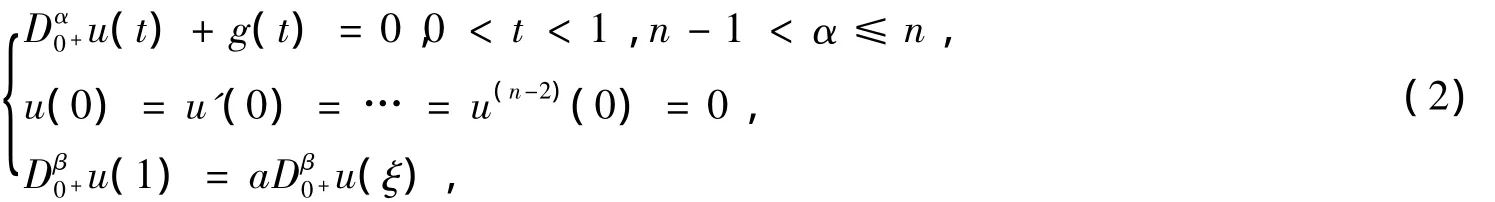
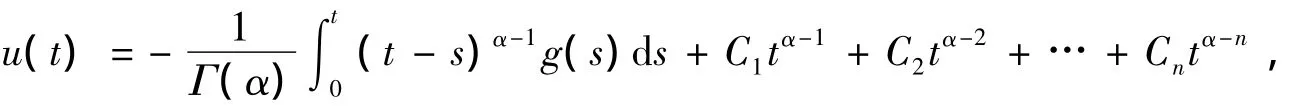
再根据引理2有

又由边值条件D0β+u(1)=aD0β+u(ξ)得

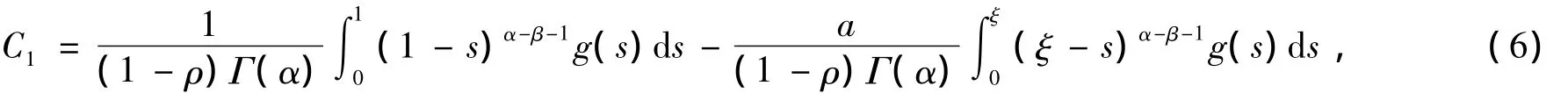
从而将(6)式代入(5)式即可得所证结果．

引理4 函数G1(t，s)具有下列性质:

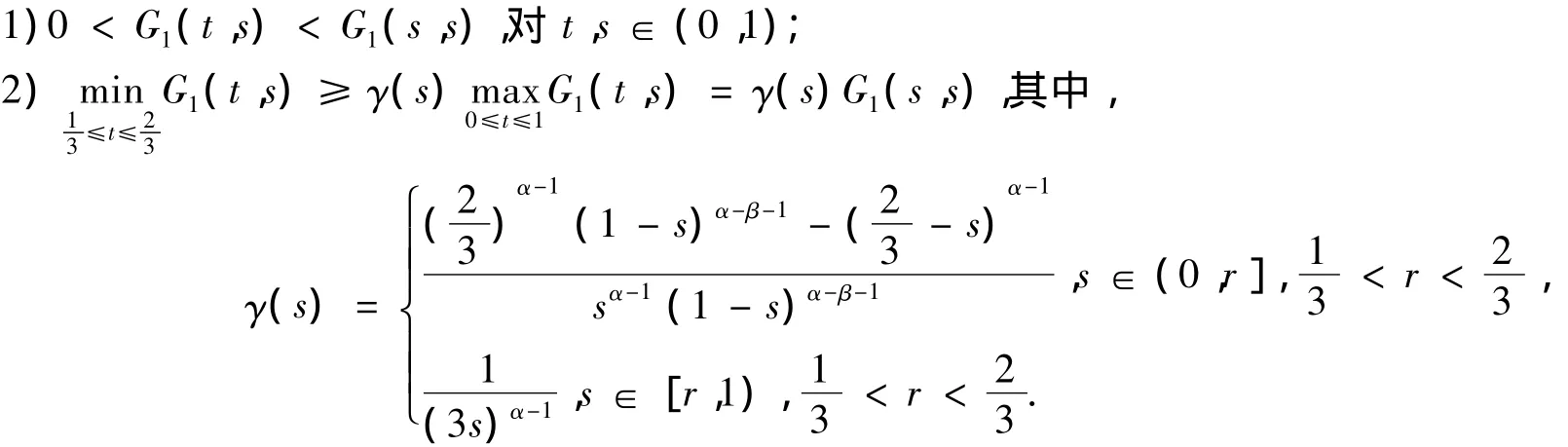
引理5 函数G2(t，s)具有下列性质:

证明过程参考文献［12］．

下面考虑非线性分数阶高阶微分方程边值问题(1)的正解的存在性，先引入Banach空间并定义几个算子．

设空间E=C［0，1］表示由全体连续函数u构成的Banach空间，其中范数?，定义E=C［0，1］中的锥 P={u ∈ E:u(t)≥ 0}，t∈［0，1］．

对给定的正数r，定义函数空间Ωr={u∈C［0，1］:u ＜r}，极大数Mr{f(t，u):(t，u)∈［0，1］× ［－ r，r］}，又 λ(t)在 t∈［0，1］上连续，从而存在正数 ω ＞ η ＞ 0，使得 η ＜ λ(t)＜ ω．

引理6 (Banach不动点定理)设E是Banach空间X的非空闭子集，T:E→E为E上的压缩映射，则T有唯一的不动点x∈E，使得Tx=x．

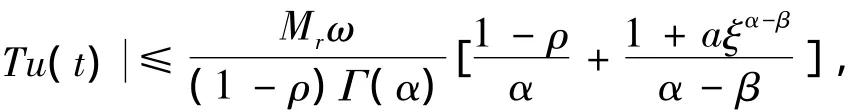
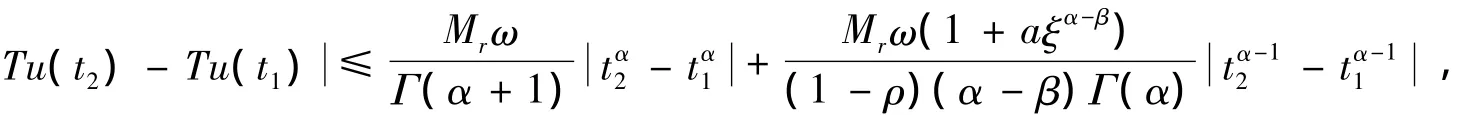
当t1→t2时所以，T是全连续算子．证毕．

下面给出下列条件:

H1(i)f(t，u(t))在t∈［0，1］上是勒贝格可测的;(ii)f(t，u(t))对u(t)∈［0，∞)上是连续的．

H2存在一个实数函数h(t)∈L［0，1］，对任意u，v∈［0，∞)有

定理1 如果条件H1和H2成立，且

则边值问题(1)在t∈［0，1］上存在唯一的正解．证明 对算子T，任意u，v∈P，有

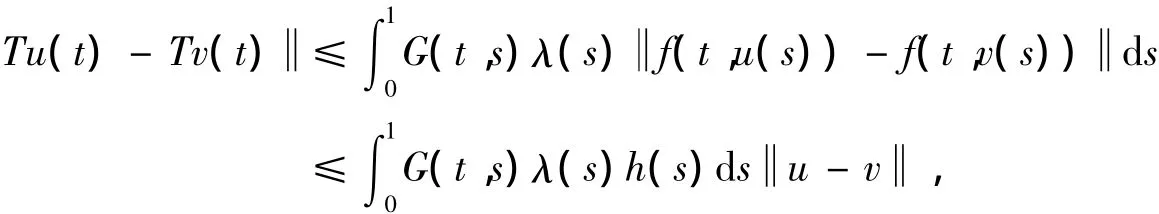
即T是压缩映射，从而存在唯一的不动点即为边值问题(1)的唯一正解．证毕．

为了证明边值问题(1)至少存在一个正解，给出引理8．

引理8 (Guo-Krasnosel’skii不动点定理)设P为Banach空间E的锥，Ω1，Ω2是E中的有界集，0∈Ω2∩Ω1，这里0表示E中的零元，T在P∩(Ω2Ω1)至少存在一个不动点，如果T:P∩(Ω2Ω1)→P是全连续算子且满足下列条件之一:

为了方便，记

定理2 假设存在正数r1＜r2且Nr1＜Lr2，并满足下列条件:则边值问题(1)至少存在一个正解u，满足r1≤ u ≤r2．

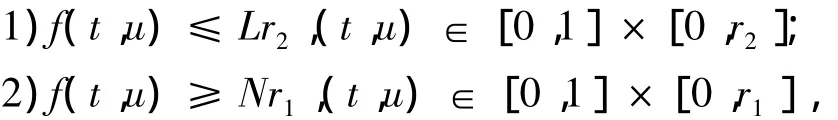
对 u∈ P ∩ ∂Ω2，t∈［0，1］，由引理5 ～ 6及条件1)可得

即 Tu ≤ u ，当u∈P∩ ∂Ω2．

即 Tu ≥ u ，当u∈P∩∂Ω1．因此算子T满足引理8的条件2)，从而算子T至少存在一个不动点u，且

满足r1≤ u ≤r2，而u即是边值问题(1)的正解．证毕．

3 应用例子

例 令n=3，则α∈(2，3］，考虑分数阶积分微分方程

［1］ Oldham K B，Spanier J.The Fractional Calculus［M］.New York:Academic Press，1974:181-195.

［2］ Hilfer R.Applications of Fractional Calculus in Physics［M］.Singapore:World Scientific，2000:50-377.

［3］ Lakshmikantham V，Leela S，Vasundhara Devi J.Theory of Fractional Dynamic systems［M］.Cambridge:Cambridge Academic Publishers，2009:5-60.

［4］ 晏祥玉，周激流.分数阶微积分在医学图像处理中的应用［J］.成都信息工程学院学报，2008，23(1):38-41.

［5］ 刘式达，时少英，刘式适，等.天气和气候之间的桥梁:分数阶导数［J］.气象科技，2007，35(1):15-19.

［6］ 韦煜明，王勇，唐艳秋，等.具p-Laplace算子时滞微分方程边值问题解的存在唯一性［J］.广西师范大学学报:自然科学版，2012，48(5):48-53.

［7］ Ma Junchi，Yang Jun.Existence of solutions for multi-point boundary value problem of fractional q-differential equation ［J］.Electronic Journal of Qualitative Theory of Differential Equations，2011，2011:1-10.

［8］ Ma Junchi，Yang Jun.Existence and uniqueness of solutions for multi-point fractional boundary value problems for nonlinear fractional integral-differential equations［J］.Mathematica Applicata，2011，24(3):575-580.

［9］ 杨军，马俊驰，赵硕，等.分数阶微分方程多点分数阶边值问题［J］.数学实践与认识，2011，41(11):188-194.

［10］ Bai Zhanbing，LÜ Haishen.Positive solutions for boundary value problem of nonlinear fractional differential equation ［J］.J Math Anal Appl，2005，311(2):495-505.

［11］ 王翠菁，刘文斌，张金陵.非线性分数阶微分方程边值问题解的唯一性［J］.河南科技大学学报:自然科学版，2013，34(1):85-88.

［12］ Li Chengfu，Luo Xiannan，Zhou Yong.Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations［J］.Computers and Mathematics with Applications，2010，59(3):1363-1375.