关于不定方程组x±1=6pqu2，x2∓x+1=3υ2 的整数解

杜先存， 孙映成， 万 飞

(1．红河学院 教师教育学院 云南蒙自661199;2．盐城师范学院数学科学学院 江苏盐城224002)

0 引言

关于三次不定方程

的整数解的问题一直是数论研究者关注的问题．文献［1－5］给出了一些结果．

就起着重要的作用．然而关于不定方程组(2)的整数解的情况，目前仅就D为素数时，有一些结论:文献［6］得出了方程组x+1=6Du2，x2－x+1=3v2无正整数解;文献［7］得出了x－1=6Du2，x2+x+1=3v2仅有整数解(D，x，u，v)=(D，1，0，±1)，(13，313，±2，±181)．

本文将利用递归序列、Pell方程的解的性质、Maple小程序，得出当D含两个互异的6k+1型素因子时方程组(2)的解的情况．

1 主要引理

引理1［8］设p是一个奇素数，则丢番图方程4x4－py2=1除开p=3，x=y=1和p=7，x=2，y=3外，无其他的正整数解．

引理2［8］方程 x2－3y4=1 仅有整数解

2 主要定理及证明

定理1 设p，q为互异的奇素数，p≡q≡1(mod 6)，则不定方程组

只有平凡解(x，u，v)=(1，0，±1)．

证明 1)先证存在性

将式(3)的x=1+6pqu2代入x2+x+1=3v2，整理得

设(xn，yn)(n∈Z)为Pell方程X2－3Y2=1的任意整数解，显然 2 +是Pell方程X2－3Y2=1的基本解．于是式(4)的一切整数解可表示为

因此，4pqu2+1= ±yn(n∈Z)，即4pqu2= ±yn－1．又 y－n= －yn，所以只需考虑

由式(5)，得 yn≡1(mod 4)．

容易验证下列各式成立:

对递归序列(6)取模4，得周期为4的剩余类序列，且仅当n≡1(mod 4)时，有yn≡1(mod 4)，所以只有当n≡1(mod 4)时式(5)才成立．

当 n≡1(mod 4)时，不妨令 n=4m+1(m∈Z)，则由式(5)、(7)和(8)得

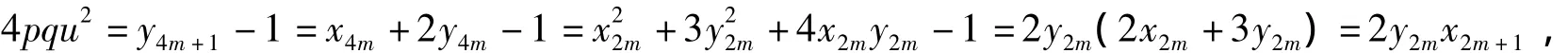
即2pqu2=x2m+1y2m．

由式(7)得，gcd(x2m+1，y2m)=gcd(2x2m+3y2m，y2m)=gcd(2x2m，y2m)=gcd(2，y2m)=2．又由式(9)、(10)得，x2m+1≡2(mod 4)，y2m≡0(mod 4)，所以下列情形之一成立:

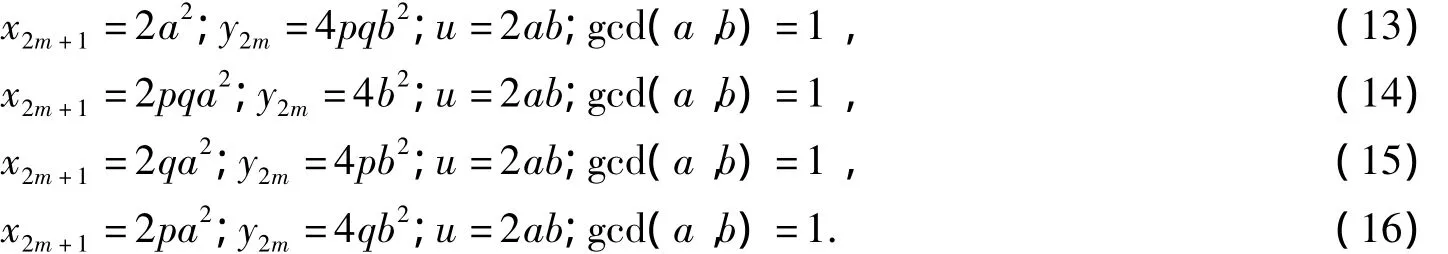
将式(13)中x2m+1=2a2代入x22m+1－3y22m+1=1，得4a4－3y22m+1=1．根据引理1知，a= ±1，此时x2m+1=2，则 m=0．再由式(6)得 y0=0，故由式(13)中 y2m=4pqb2，得 4pqb2=0，则 b=0，故 u=0，于是得到方程组(3)的平凡解(x，u，v)=(1，0，±1)．

2)再证唯一性

由式(14)的 y2m=4b2得 xmym=2b2，又由式(10)知 ym≢2(mod 4)，而 gcd(xm，ym)=1，故 xm=2c2，ym=d2，因此有4c4－3y2m=1．根据引理1 知，c= ±1，ym= ±1．则由 c= ±1 得，xm=2，故 m=1．此时由式(11)得x3=26，故由式(14)的 x2m+1=2pqa2，得26=2pqa2，所以 a=1，pq=13，这与“p，q为互异的奇素数”矛盾．所以该情形方程组(3)无整数解．

由式(15)的y2m=4pb2得xmym=2pb2，又由式(10)知ym≢2(mod 4)，而 gcd(xm，ym)=1，所以下列情形之一成立:

若式(17)成立，则有4c4－3y2m=1．由引理1 知，ym= ±1，则由式(18)ym=pd2，得1=pd2，则有p=1，这与“p为奇素数”矛盾，所以该情形方程组(3)无整数解．

若式(18)成立，则有 x2m－3d4=1．由引理2 知，xm= ±1，±2，±7，故由式(18)xm=2pc2，有 2pc2=2，则p=1，这与“p为奇素数”矛盾，所以该情形方程组(3)无整数解．

由式(16)的y2m=4qb2，仿式(15)的讨论知，该情形方程组(3)无整数解．

综上1)和2)可知，定理1成立．

从2018年初开始，合作社不再聘请执行理事，所有经营管理由村两委负责。合作社每年将召开全体成员大会一次，向全体社员汇报年度的重要工作、财务收支、股权分红以及下一年度工作计划。

定理2 设p，q为互异的奇素数，p≡q≡1(mod 6)，则不定方程组

仅有平凡解(x，u，v)=(－1，0，±1)．

事实上，将x=6pqu2－1代入x2－x+1=3v2，整理得

仿照定理1的证明可知式(20)的一切整数解可表示为

为此也只需考虑

由式(21)，得 yn≡ －1(mod 4)．

对递归序列(6)取模4，得周期为4的剩余类序列，且仅当n≡－1(mod 4)时，有yn≡－1(mod 4)，所以只有当n≡－1(mod 4)时式(21)才成立．

当 n≡ －1(mod 4)，令 n=4m －1(m∈Z)，则由(8)、(12)和(21)得

即

由式(6)知仅当m=0时，y2m=0．又由式(11)知对于任意整数m，均有x2m－1≠0，所以仅当 m=0时，x2m－1y2m=0．

(i)m=0 时，由式(22)得，u=0，此时得出方程组(19)的平凡解(x，u，v)=(－1，0，±1)．

(ii)m≠0时，仿定理1的证明可知不定方程组(19)无整数解．

综上，定理成立．

对于方程组(2)的整数解的情况，本文仅仅给出了D含两个互异的6k+1形素因子时的解的情况，对于D含3个及以上互异的6k+1形素因子时方程组(2)的解的情况还有待于进一步研究．

［1］ 柯召，孙琦．关于丢番图方程 x3±1=Dy2［J］．中国科学，1981，24(12):1453 －1457．

［2］ 黄寿生．关于指数 Diophantine方程 x3－1=2py2［J］．数学研究与评论，2007，27(3):664 －666．

［3］ 管训贵．关于 Diophantine方程x3±1=2py2［J］．云南民族大学学报:自然科学版，2012，21(6):438 －441．

［4］ 张海燕，王连芳．关于丢番图方程x3±1=2Dy2［J］．哈尔滨理工大学学报:自然科学版，1997，2(6):85 －87．

［5］ 杜先存，赵东晋，赵金娥．关于不定方程x3±1=2py2［J］．曲阜师范大学学报:自然科学版，2013，39(1):42－43．

［6］ 田晓霞．关于不定方程组 x+1=6py2，x2－x+1=3z2［J］．四川理工学院学报，2009，22(1):30 －31．

［7］ 牟全武．对文“关于指数Diophantine方程x3－1=2py2”的注记［J］．西安文理学院学报:自然科学版，2008，11(4):43 －45．

［8］ 曹珍富．丢番图方程引论［M］．哈尔滨:哈尔滨工业大学出版社，1989．