固定设计下时间序列非参数回归模型的方差变点检验

孙耀东， 徐 宝， 赵志文

(吉林师范大学数学学院 吉林四平136000)

} ，其中

，故

定理1设条件1)～4)成立，在H0为真时

0 引言

考虑如下时间序列非参数回归模型的方差变点检验，

其中xt=t/n是等距固定设计点，g是定义在［0，1］上的回归函数，{εt}为零均值和有限方差σ2的严平稳α－强混合序列，检验问题为

H0:E(ε2t)=σ2，对所有的 t=0，1，2，…，n;H1:H0不成立．

一般认为，变点问题的研究始于1954年［1］，从20世纪60年代后期开始，有更多的统计学者投入到这一研究领域，文献［2］就是对这一领域近20年来理论问题的总结．时间序列在经济、金融等领域中有重要应用［3］，关于时间序列的方差变点问题变得越来越重要［4－7］．

本文采用文献［8］提出的Beta-Bernstein光滑方法估计回归函数研究模型(1)的检验问题，Beta-Bernstein光滑方法克服了文献［6］中经典核方法的有边界偏差的缺点，在一定条件下可以提高检验效果．

1 主要结果

应用Beta-Bernstein方法估计模型(1)中的回归函数g(·)，估计量为，其中，这里 Kα，β是 Beta 分布 Beta(α，β)的密度函数，λ 为光滑参数，1/λ 类似于经典核估计的窗宽，满足．记残差的估计量为

} ，其中

定义CUSUM检验统计量为Tn为得到统计量Tn的极限性质，需要以下假设:

1){εt}是 α － 强混合序列，且存在C ＞ 0，ρ＞0使得混合系数αk≤Ce－ρk，E(εt)=0，存在r＞2使得

2)g(·)具有连续二阶导数，g(·)是Lipschitz连续的，即存在K1＞0，对0≤x，y≤1，使 g(x)－g(y)＜1

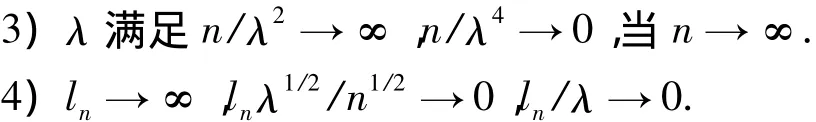
引理1［9］当1)成立，在H为真时

0

引理2 当1)～3)成立，在H0为真时

中C1为常数，从而式(3)第一项为，其．由文献，式(3)的第二项为O

A－A．12为常数

，故

引理3当1)～4)成立，在H0为真时

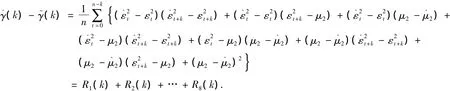
由Schwarz不等式，

对 i=2，4 有

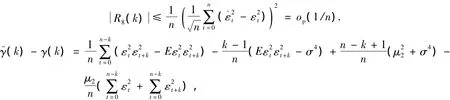
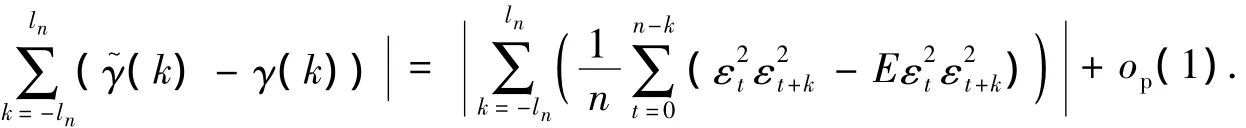
由文献［11］

定理1设条件1)～4)成立，在H0为真时

2 数值模拟

考虑如下数据生成过程 yt=g(xt)+ εt，εt= φεt－1+et，xt=t/n，t=0，1，2，…，n，g(xt)=25x3t－45x2t+24xt－3．6，et是均值为0、方差为 σ2的独立同分布正态随机变量，取 ln=［n1/4］，λ =［n1/3］．假定方差变点发生的时刻为 t0=［nτ0］，检验问题如下:

H0:σ2=1，对所有的 i=1，2，…，n;H1:σ2在 t0=［nτ0］之前为 1，之后为 α2．

其中 α2取值为2，4，9，τ0取值0．5，φ 取值0，0．3，0．5，0．8，样本容量 n=100，200，300，见表1．实验重复1 000次，在0．05的显著性水平下计算拒绝原假设的频率．通过随机模拟，在0．05检验水平下，检验的临界值为1．36．通过模拟结果可以看出检验是一致的，样本容量n越大，检验效果越好，并且当n足够大时，检验的势函数值趋近于1．变点后的方差α2越大，检验效果越好．另外，检验效果与自回归系数φ有关，随着φ增大接近1，自回归模型趋近非平稳，检验效果相对较差．由于文献［6］的非参数估计方法需要删掉部分样本信息，在样本量不大时本文结果相对较好，当样本量增大时，本文结果与文献［6］的结果相差不大．