基于推进剂复杂本构模型的药柱结构分析模块开发①

唐国金,邓 斌,申志彬

(国防科技大学 航天科学与工程学院,长沙 410073)

0 引言

固体发动机药柱在长期服役过程中会发生化学老化，并在长期载荷作用下可能导致力学损伤。此外，推进剂是典型的粘弹性材料，其泊松比为时间的函数[1]。因此，药柱精细结构完整性分析需考虑推进剂变泊松比、老化及损伤等效应的影响。

老化和损伤是导致推进剂本构非线性的两大主要因素。关于推进剂含老化或损伤粘弹性本构理论，目前已有较多研究成果[2-6]。这些研究工作多采用定泊松比模型，即将泊松比视为常数，未考虑粘弹性材料泊松比的时间相关性，且这些本构理论尚未很好地实现工程应用。众所周知，泊松比参数的选取对药柱结构响应结果影响显著。因此，为更准确地进行药柱结构分析，有必要进一步开展考虑变泊松比、老化和损伤效应的粘弹性本构模型的分析方法及工程应用研究。

开展药柱老化损伤结构分析需采用含老化和损伤的本构模型，但分析过程涉及大量的非线性方程组求解运算，往往需要采用有限元法进行求解[7]。国内有学者[8-9]利用有限元法对含损伤粘弹性本构模型进行了研究，实现了简单平面问题的应用分析，但对于三维复杂结构的有限元分析问题，由于涉及到复杂的前后处理、单元构建以及大量非线性求解运算等问题，完全自主编程实现代价巨大，且也难以满足面向工程应用的需求。

利用Abaqus、Marc等商用有限元软件，可对药柱进行线粘弹性分析，但无法考虑变泊松比、老化和损伤效应等的影响。然而，它们提供了用户材料模型二次开发功能。一些学者[10-12]通过商业有限元软件的二次开发技术，实现了非线性粘弹性本构模型的有限元计算，并取得了良好的效果。本文通过建立一种考虑变泊松比、老化和损伤效应的三维粘弹性本构模型，采用增量有限元法对其进行数值离散，同时为实现该本构模型有效应用于工程实践，基于Abaqus软件的二次开发技术编写了相应的材料子程序，并在已有的“发动机结构分析系统”[13]基础上，开发可同时考虑推进剂变泊松比、老化和损伤效应的药柱结构分析模块。

1 一种新型粘弹性本构模型

1.1 推进剂老化发展方程

对于丁羟推进剂等高聚物材料，可采用交联度近似地表征其化学老化过程。交联度υ的发展方程一般可采用如下形式[3]

(1)

其中

式中t′为老化时间；T为老化温度；Ea为老化反应的活化能；k为Boltzmann常数；h为Planck常数；α为化学配分函数待定系数；A为化学反应速率常数；υ0为初始交联度；υm为最大交联度。

1.2 推进剂损伤发展方程

用ω表示推进剂损伤，其发展方程可取为[3]

(2)

式中σ*为当量应力。

g(x)函数具有如下形式

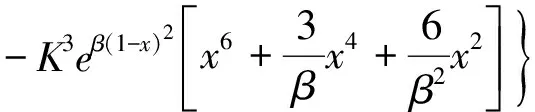
g(x)=0 (x>1)

式中γ、K、β和σth为与损伤相关的材料常数。

在损伤各向同性假设下，当量应力σ*可采用如下形式[14]

其中

1.3 含老化和损伤的热粘弹性本构方程

根据由松弛模量E和泊松比ν表示的线粘弹性本构模型[1]，考虑推进剂老化和损伤的影响[3，14]，并假设老化时间与加载时间起点相同(取式(1)中t′=t)，综合可得含老化和损伤效应的推进剂三维热粘弹性本构方程为

(3)

(4)

(5)

温度平移因子aT满足WLF方程

(6)

式中C1和C2为材料常数；T为当前温度，T0为参考温度。

式(4)中的泊松比ν和含老化松弛模量E的形式分别为

(7)

(8)

对于式(3)所示的本构方程，如果考虑材料在加载前已老化了时间td，则根据式(1)可知，只需将式(1)中的系数B等效替换成Be-β(td,T)，此时的本构方程(3)即可考虑加载之前的老化效应。

2 数值计算模型

2.1 本构方程的增量形式

下面采用增量法对本构模型进行数值离散。将分析时间[0,t]划分为[ti-1,ti](i=1,2,…,M)共M个子区间。在各增量步内，假设有效应力和应变均随折算时间ξ′呈线性变化，采用积分算法对式(3)～(5)进行数值离散，并结合有效应力形式，最终可得到在时间步[tm,tm+1]内的本构增量形式为

(9)

(10)

(11)

(12)

式中

(13)

(14)

(15)

(16)

(17)

式中

(18)

其中

(19)

(20)

(21)

(22)

(23)

2.2 本构方程的切线刚度

利用一致切线刚度(Jacobian)，可保证Abaqus计算所采用的Newton法具有二阶收敛速率。根据切线刚度的定义，对于小变形或者小体变的大变形问题，其一致切线刚度的形式为[7]

(24)

综合式(9)和(24)，可得到tm+1时刻的一致切线刚度，其各个分量为

式中

对于各向同性材料，具有如下的关系式

C2222(tm+1)=C3333(tm+1)=C1111(tm+1)

C2233(tm+1)=C1133(tm+1)=C1122(tm+1)

C2323(tm+1)=C1313(tm+1)=C1212(tm+1)

2.3 应力更新方法

针对增量型本构方程(9)，将其进一步改写成

(25)

令

则方程组(25)可简写成

σij(tm+1)+Dij(tm+1){ωm+1[σij(tm+1)]-1}=0

(26)

式(26)是以应力为变量的非线性方程组，对此一般需采用迭代法进行求解。本文拟采用Newton法[7]进行求解，进而可实现当前应力等的更新。

3 新型本构模型的二次开发

3.1 Abaqus材料子程序开发

为实现新型材料本构模型的Abaqus二次开发，用户需通过其UMAT(User-defined Mechanical Material Behavior)接口开发相应的材料子程序。针对上文给出的考虑变泊松比的含老化和损伤粘弹性本构数值模型，开发了相应的材料子程序，其基本实现流程如图1所示。

实现的主要思路：根据主程序(Abaqus)提供的初始应力、应变、应变增量、温度以及材料参数等相关信息，材料子程序先后完成含老化和损伤的非线性方程组数值求解，实现当前时刻的应力和状态变量等的更新，最后向主程序返回当前应力、本构的一致切线刚度以及状态变量等变量。

图1 材料子程序实现流程图

3.2 药柱结构分析模块开发

在“发动机结构分析软件系统”[13]的基础上，进一步嵌入本文含老化和损伤的药柱结构分析模块。该模块可实现用户材料参数的输入、材料子程序与求解器的连接、计算提交及结果后处理等功能，其分析过程关键的图形化交互操作界面如图2～图4所示。

图2 药柱结构分析模块主菜单

为满足不同平台下的分析需要，开发了Abaqus和Marc 2种不同环境下的求解模块(图3)。用户可根据需要选择不同的本构模型和求解器来进行计算。通过将开发的材料子程序以及分析模块集成到综合软件分析系统中，可充分利用商用有限元软件的强大前后处理和求解能力，方便地实现实际型号固体火箭发动机的工程应用分析。

(a)结构分析主面板 (b)用户材料参数设置

图4 松弛模量参数输入界面

4 分析模块在药柱结构分析中的应用

下面利用上述所得药柱结构分析模块应用于实际型号发动机药柱结构分析。

以某固体发动机为研究对象，根据其载荷和结构对称性，取其1/12结构建立图5所示有限元模型。式(8)所示的含老化松弛模量各系数如表 1所示，式(7)所示的变泊松比取5项时的系数如表 2所示，其他材料参数见表 3。

图5 药柱有限元模型

n0123τEn/s—5.295 5252.955 2529.552E0n/MPa5.933 40.956 90.697 20.509 7E1n/MPa7.328 50.857 11.599 31.200 5

表2 泊松比v(t)的 Prony 级数系数

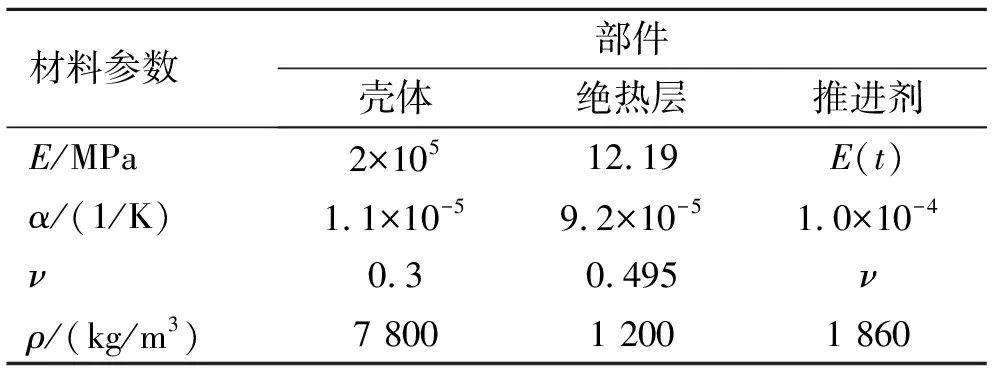
表3 其他材料参数

取式(1)中的交联度发展方程系数A=6.95×10-12，α=-8 710，υ0=3.13×10-5mol/ml，υm=1.012×10-4mol/ml、Ea=7.438×10-20J；式(6)中的WLF方程参数C1=4.97，C2=156.1，T0=293.15 K；损伤参数σth=1.82 MPa(受压)，γ=1.046，K=0.1，β=0.5。

载荷工况：先后经历1 d的固化降温、10 a的20 ℃恒温贮存，以及0.5 s的地面点火增压过程。其中，固化降温过程为从零应力的T1=58 ℃自然降温到T0=20 ℃，温度变化近似服从规律[15]

T(t)=TI-(TI-T0)(1-e-6.8×10-5t)

(27)

在点火增压过程，对其内表面施加均布压力载荷：p(t)=6(1-e-20t)MPa。

计算时约束模型的环向位移，并先后采用表 4 所示的8种不同效应的本构模型，计算上述过程药柱的结构响应。表 4中，标“√”为含有该效应；标“×”为不含有该效应。以模型8的计算结果为例，给出点火增压结束时的药柱Von Mises应力(MPa)和损伤分布图，分别如图6和图7所示。

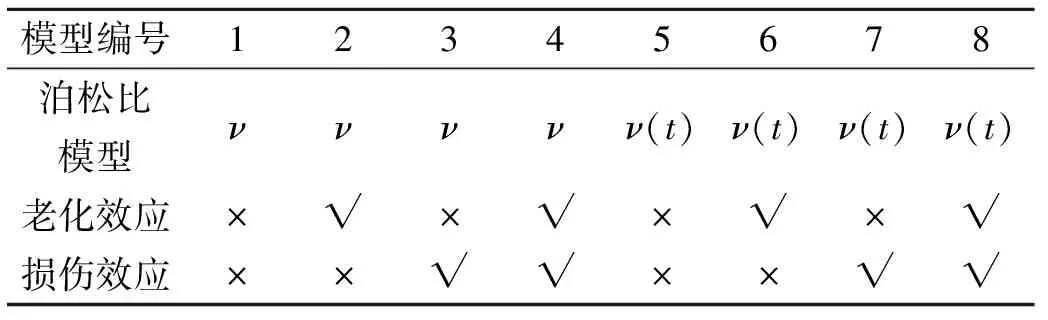
表4 采用的本构模型

图6 药柱Von Mises应力分布图

图7 药柱损伤分布图

由图6和图7可知，药柱Von Mises应力在内表面的过渡段和圆管段部位较大，而损伤主要发生在Von Mises应力较大的区域，且几乎集中在过渡段，这与式(2)中的损伤为Von Mises应力的单调非递减函数是相符的。以药柱内表面结果为例，取圆管段P1和过渡段P2两个关键部位为例(见图6)，其在增压过程第0.5 s时的Von Mises应力、Von Mises应变及损伤对比结果见表 5。根据表 5，采用定泊松比模型的计算结果中，(以P2处的结果为例)，在同等条件下考虑老化效应模型比不考虑老化效应模型所得Von Mises应力要高出约14%，而Von Mises应变却减少了约34%，这主要是由于老化效应导致推进剂模量上升引起的。在同等条件下，考虑损伤比不考虑损伤时得到的Von Mises应力有所减小，而Von Mises应变却有所增加。这是因为损伤效应体现了推进剂的“软化”效应，使其有效模量减小引起的。对于采用变泊松模型所得相应结果也有上述类似结论。

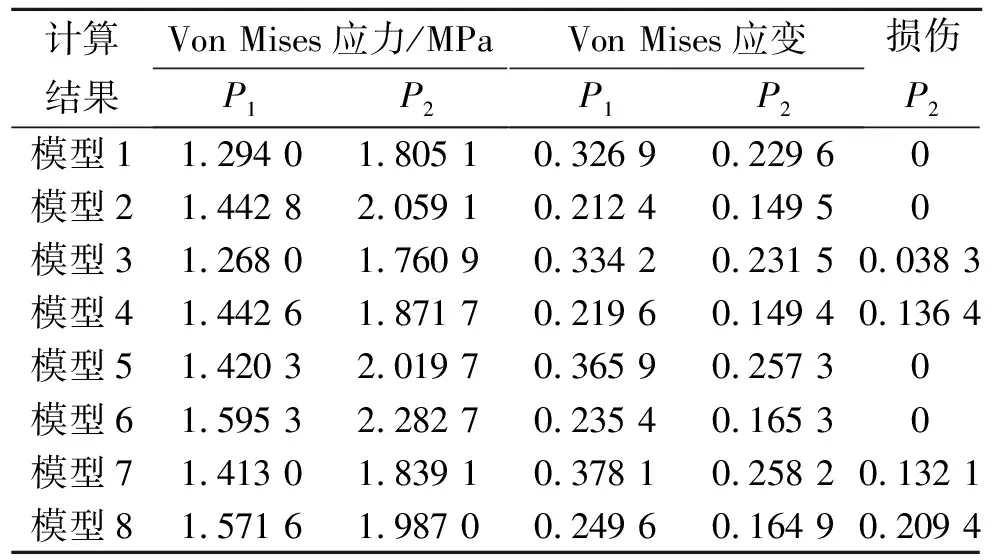
表5 不同模型下的计算结果对比

对比采用变泊松比和定泊松比模型所得结果差异发现，在同等情况下，变泊松比模型下对应的应力、应变结果均相对较大。这主要是由于采用传统的定泊松比模型分析时，其泊松比一般取值在较大的0.490～0.499之间，而本文变泊松比的取值在0.482～0.494之间(0.5 s内)，取值相对较小，但其应力、应变结果均却相对较大，所得结果满足泊松比越小、其应力和应变结果越大的规律。

综上可知，推进剂的力学性能受老化和损伤效应等的影响显著，老化效应可导致材料“硬“化，而损伤效应导致材料“软”化。因此，相比于传统线粘弹性本构模型，本文含老化和损伤的本构模型可更准确地体现推进剂的实际力学性能变化。

5 结论

(1)相比于传统线粘弹性本构模型，本文的粘弹性本构模型体现了粘弹性泊松比的时间相关性，同时考虑了老化和损伤效应，适合于发动机长期服役过程中不同载荷下的药柱结构分析，具有实用价值。

(2)采用有限元法对该新型本构模型进行了数值分析，并基于商用有限元软件的二次开发技术，创建了材料子程序，实现了复杂粘弹性本构模型的三维有限元分析。研究方法对粘弹性本构一类问题的分析具有通用性。

(3)将药柱结构分析模块集成到统一的发动机综合分析系统中，结合实际载荷工况，可实现具体型号发动机结构分析。研究工作为进一步分析固体发动机药柱精细结构完整性与寿命评估提供了技术支撑，具有工程应用价值。

参考文献：

[1] 赵伯华. 固体推进剂粘弹泊松比的研究[J].北京理工大学学报,1994,14(1):87-90.

[2] Schapery R A.A micromechanical model for non-linear viscoelastic behavior of particle-reinforced rubber with distributed damage[J].Engineering Fracture Mechanics,1986,25(5):845-867.

[3] 周建平. 化学不稳定的工程材料的粘弹性损伤本构模型 [D].长沙: 国防科技大学,1989.

[4] Zhou J P.A constitutive model of polymer materials including chemical ageing and mechanical damage and its experimental verification[J].Polymer,1993,34(20):4252-4256.

[5] 彭威,周建平,任钧国.复合固体推进剂非线性粘弹本构方程的微观力学分析[J].固体火箭技术,1999,22(4):23-25.

[6] 阳建红,俞茂宏,候根良,等.HTPB复合固体推进剂含损伤和老化本构研究[J].推进技术,2002,23(6):509-512.

[7] Zienkiewicz O C,Taylor R L. The finite element method for solid and structural mechanics (Sixth edition)[M].Oxford: Elsevier Butterworth-Heinemann publications,2005.

[8] 冯志刚,周建平.粘弹性有限元法研究[J].上海力学,1995,16(1):20-26.

[9] 杜建科,朱祖念,张善祁,等.固体火箭发动机药柱损伤粘弹性有限元分析[J].固体火箭技术,2001,24(1):1-6

[10] Hinterhoelzl R M,Schapery R A. FEM implementation of a three-dimensional viscoelastic constitutive model for particulate composites with damage growth[J].Mechanics of time-dependent materials,2004,8(1):65-94.

[11] Masad E,Huang C W,Airey G,et al.Nonlinear viscoelastic analysis of unaged and aged asphalt binders[J].Construction and Building Materials,2008,22:2170-2179.

[12] 孟红磊,鞠玉涛.含损伤非线性粘弹性本构模型及其数值仿真应用[J].固体火箭技术,2012,35(6):764-772.

[13] 申志彬,李磊,段静波,等.基于Patran二次开发的固体发动机结构分析系统[J].固体火箭技术,2011,34(2):171-175.

[14] Lemaitre J. A course on damage mechanics[M].Berlin:Springer,1992.

[15] 李磊. 基于结构完整性分析的固体火箭发动机药形改进与优化设计[D].长沙:国防科技大学,2011.