基于主应力的固体火箭发动机界面累积损伤分布研究①

邱 欣，李高春，张春龙，杨 明

(1.海军航空工程学院 研究生管理大队，烟台 264001；2.海军航空工程学院 飞行器工程系，烟台 264001)

0 引言

固体火箭发动机使用寿命的确定具有重要的军事价值，国外已开展了大量固体火箭发动机寿命预估项目[1-3]。试验发现，推进剂、衬层、绝热层界面脱粘是多种型号发动机的失效模式之一，而环境温度的变化是造成装药损伤的重要原因[4]。通过工业CT可有效分辨发动机界面是否脱粘，但不能确定未脱粘界面粘连剩余强度的大小，利用累积损伤理论计算发动机装药损伤程度是目前较常用的方法[5-6]，文献[7-9]发展了多种累积损伤的计算形式，该方法也可近似计算装药粘接界面的剩余强度。

国内大多采用畸变能密度强度理论(第四强度理论)，对装药结构完整性进行校核[10]，该强度理论对拉压流动极限相等的材料计算精度较高。由于推进剂及其界面粘接系统的抗拉强度明显小于抗压强度，因此基于该理论的计算结果需要进一步验证。

存在于界面上的应力包含拉应力与剪应力，采用单纯拉伸与剪切试验可判断界面力学性能[11]，但在实际情况中，两种应力同时存在，将单一载荷试验结果线性叠加，可用于混合载荷的计算，但通过设计不同载荷角度的拉伸试验更符合实际情况[12]。可采用主应力的方法计算界面损伤，包含载荷的大小与方向，具有物理意义明确的优点，文献[13-14]采用最大主应力进行发动机装药累积损伤计算，并设计了相应试件及试验方法。

本文通过多向定载试验探索了粘接系统混合载荷条件下的失效规律，建立了包含载荷角度的界面损伤模型，根据主应力分析界面载荷及损伤情况，预估了环境温度热应力对发动机界面造成的损伤。

1 试验

1.1 试验方法

对于固体火箭发动机推进剂/衬层/绝热层界面力学性能，大多采用扯离和剪切的试验方法进行测试，可在短时间内比较不同生产配方与工艺粘接试件的力学性能。定载试验耗时较长，但在定载试验中，界面所受载荷恒定且较小，与发动机内部粘接界面实际的受力状态接近，其试验结果在实际应用中更具参考价值。

试验采用的试件粘接系统由HTPB推进剂、衬层及钢板组成。试件截面为正方形，其尺寸如图1所示。

图1 试件及其尺寸

在过去的定载试验中，试件承受的载荷均与界面垂直，考虑到发动机界面既存在垂直于界面的载荷，还存在切向载荷，即界面处合力方向与界面存在一定的夹角。为此，根据试件尺寸，设计了如图2所示的多角度拉伸夹具，可分别进行载荷角度θ(载荷方向与界面夹角)为0°、22.5°、45°、67.5°、90°时的定载试验。

(1)

图2 多角度拉伸夹具与定载计时装置

1.2 试验现象

试件挂载一段时间后，靠近衬层边缘的推进剂首先出现脱湿现象，如图3(a)所示。随着脱湿面积以及脱湿位移的增加，逐渐形成宏观裂纹，并最终导致试件在该位置断裂，如图3(b)所示。

(a)衬层边缘推进剂氧化剂颗粒脱湿

(b)界面附近推进剂裂纹形成

1.3 试验结果分析

载荷垂直于界面的定载试验结果如图4所示。试件中界面平均应力最小值为0.05 MPa，已小于文献[15]测得的实际拉伸载荷(0.069～0.138 MPa)，但仅承载了7个月，其原因可能有：化学老化导致其力学性能下降；试件衬层与钢件之间没有人工脱粘设计[11]，导致试件边缘应力明显大于平均应力，使试件边缘过早出现裂纹；在发动机中，当界面附近推进剂松弛后，所承载的拉伸应力将会下降，而试件承载的载荷不会因推进剂的蠕变而减小，反而会因截面积的减小而升高。该批试件从生产后在密封袋中贮存了5 a，化学老化的影响肯定存在，会使分析出的损伤结果偏于保守，而实际发动机服役寿命不止5 a。因此，采用贮存5 a的试件进行试验，与实际情况更为接近，结果相对合理。

图4 试件承载时间随载荷变化规律

试件承载时间的对数lgt与载荷G存在明显的线性关系，根据茹科夫断裂的分子动力学理论[16]，高聚物的宏观断裂本质是分子共价键和高分子间范得瓦尔健的破坏，并把键的断裂看作热活化过程。分子键的断裂与合并同时进行，二者有不同的反应速率，并由温度、应力和反应活化能决定，由此推得断裂时间的对数与应力大小符合如式(2)所示的线性关系：

(2)

式中tf为断裂时间；σ为应力；C、β为常数；E为反应活化能；k为波尔兹曼常数；T为温度。

根据试件尺寸，可计算不同挂载条件下的界面平均应力，试验温度为20 ℃，对试验数据进行线性拟合得式(3)：

lgt=-14σ+8.4

(3)

式中t为承载时间，s；σ为试件平均应力，MPa。

载荷恒定为4 kg，试件承载时间随载荷角度变化的试验结果如图5所示。载荷角度θ对粘接件的承载时间影响明显，4 kg载荷90°夹角条件下承载时间与10 kg载荷0°夹角条件下的承载时间相近。试件承载时间总体上服从逐渐下降的规律，但载荷角度θ为67.5°时，lgt有一个明显的上升，如果采用4次多项式进行拟合，与试验结果有较高的一致性，但也仅是一种唯象的模型，在没有较大试验数据做基础的情况下，采用线性拟合更为稳妥。考虑其原因，可能与试件边缘加工工艺有关，如试件表面覆盖了衬层的残余物，降低了试件边缘处界面应力集中程度。

采样有限元方法，计算了在不同载荷角度下试件界面附近最大主应力集中系数的分布，如图6所示。试件边缘推进剂/衬层界面(即起裂位置)有明显的应力集中现象，而且随拉伸角度增加，应力集中系数也随之增加。采用最大主应力计算的原因是文献[14]在对粘接试件进行多角度拉伸试验时，发现采用最大主应力计算得到的界面失效临界应力受载荷角度的影响最小，并认为不垂直于界面的应力会使界面沿着最大主应力受拉方向而变化。

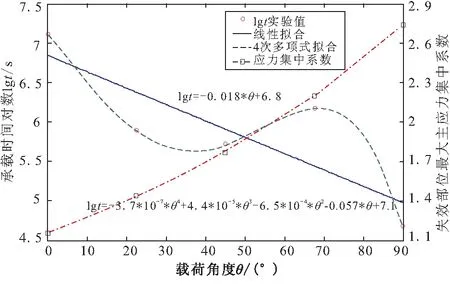
图5 试件承载时间 随载荷角度θ变化规律

图6 试件界面附近最大主应力系数分布

由于试件数量较少，试件承载时间t随载荷角度θ的准确变化规律无法获得。因此，根据试件边缘应力集中系数随载荷角度θ的线性变化过程，是较稳妥的方法，如图5所示，经线性拟合得到式(4)。

lgt=-0.018θ+6.8

(4)

由于式(3)相对式(4)更为准确，因此仅取承载时间lgt随载荷角度θ的变化斜率代入式(3)，得到式(5)所示的承载时间lgt随试件平均应力σ和载荷角度θ的变化规律。

t(σ,θ)=10-14σ-0.018θ+8.4

(5)

式中t为承载时间，s；σ为界面所受的平均应力大小，MPa；θ为载荷方向与界面法线夹角。

2 发动机界面损伤计算

2.1 环境温度

为了计算方便，近似认为年周期为360 d，每天采集2、8、14、20时的温度，则1 a共1 440个温度点，每个温度点代表6 h的平均温度。以北半球中纬度地区为例，每个温度点 近似服从式(6)所示的函数变化规律，即周期为1 a和1 d的正弦函数的叠加，每年1月和7月的平均温度分别达到最低值和最高值，每日的2时和14时的平均温度分别为最低与最高值。

(6)

式中T0为年平均温度；ΔTyear、ΔTday分别为年与日温度幅值。

为了体现实际温度的随机性，计算第i个温度点时，采用随机温度幅值，即

所计算出一年温度变化如图7所示。

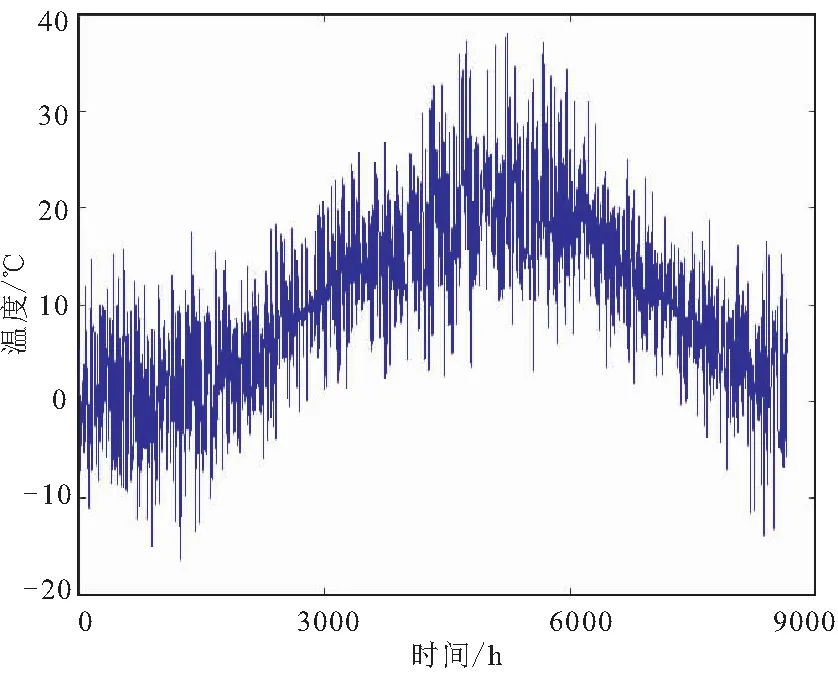
图7 1年温度的模型计算结果

2.2 计算模型

由于发动机较小，忽略重力影响，根据装药的对称性，取其1/10进行建模。通过对模型进行分割，划分了11 168个6面体网格和616个4面体网格，如图8所示。

由于本文的主要研究目标是载荷角度对界面造成的损伤，因此对装药热应力的传热计算过程进行了简化。由于计算时温度每天采集4个温度点，即假设6 h内温度不变，从而在计算时将推进剂近似视为弹性材料，模量取其平衡模量，并假设发动机装药内部温度均匀与环境温度相同，根据文献[14]的实测数据，计算时假设装药零应力温度为45 ℃，分别计算装药-20～40 ℃(间隔5 ℃)一系列稳定后的应力场，其余温度下的应力场通过插值获得。发动机各参数如表1所示。

图8 计算模型网格划分

参数壳体衬层推进剂弹性模量/MPa2.069×1051.51.89泊松比 0.2850.4950.495热膨胀系数/K-11.1×10-59.8×10-59.2×10-5

2.3 界面附近主应力分布

由于通过定载试验发现，试件的失效部位在衬层附近的推进剂内。因此，分析了紧贴衬层经过星根截面一层推进剂网格内的主应力。图9为该层推进剂在-20 ℃时主应力的分布，其分布特征如下：

(1)第1与第2主应力交替出现在垂直于界面的平面内。第1主应力主要在发动机头部顶端、圆柱段靠近前、后封头的部位，第2主应力则主要在圆柱段中部以及前封头靠近柱状段的部分，并在一定的偏转角度下对界面起到扯离作用。

(2)第3主应力始终出现在垂直于界面的平面内，在发动机头部基本垂直于粘接界面，因此界面处的第3主应力全部对界面起到扯离作用。

(3)发动机尾部人工脱粘层释放了界面应力，该位置各主应力较小。

根据第1、第2主应力方向的交替变化，将界面分为6段进行计算，取垂直于界面的发动机纵向截面内两个主应力的合力，如图10所示。在各段间的衔接部位，则取第1、第2、主应力合力在纵向截面内的分量进行计算，并假设发动机周向的主应力对界面的影响可忽略。根据所取主应力合力的大小及其与界面夹角，进行下一步发动机界面累积损伤计算。

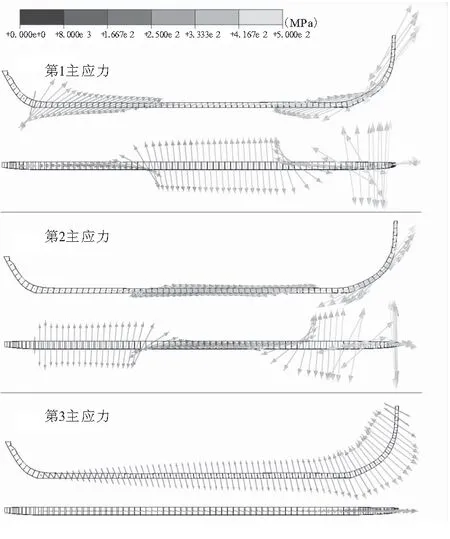
图9 -20 ℃时与衬层相邻推进剂主应力的大小及方向

图10 主应力分段计算方案

2.4 界面损伤计算

将界面某处受连续变化的应力离散化，近似得到n个大小不同的应力水平(σ1,σ2,…,σn)，以及n个应力对应的持续时间(t1,t2,…,tn)。根据线性累积损伤模型，假设各应力造成的损伤与界面已产生的损伤值无关，可线性叠加，且与先后顺序无关。根据试验获得承载时间t与平均应力σ及角度θ的关系式(4)，以及线性累积损伤的蠕变形式，总累积损伤D计算式为

(7)

推进剂为粘弹性材料，高温下应力作用较短时间相当于低温下应力作用较长时间，即时温等效原理。因此，在计算不同温度下的损伤时，均要将不同温度下应力作用时间转换为试验温度(20 ℃)下的应力作用时间，除以时温等效因子αT，根据式(8)[10]所示的WLF方程，计算不同时刻下的时温等效因子αTi：

(8)

由式(7)可计算不同温度及应力条件下的损伤值。

(8)

根据已知温度下发动机内部热应力的分布，由式(6)计算得1年的温度变化，插值得到1年中发动机内部热应力的变化历程。

图11给出了发动机过星根法截面内紧贴衬层推进剂的Mises应力和主应力合力大小变化，二者均在6～8月份最小，在1月左右达到最大。发动机头部主应力合力明显大于Mises应力。

图12给出了该层推进剂内主应力合力与界面法线的夹角，发动机头部与尾部夹角较小，为40°左右。

(a)Mises 应力

(b)主应力

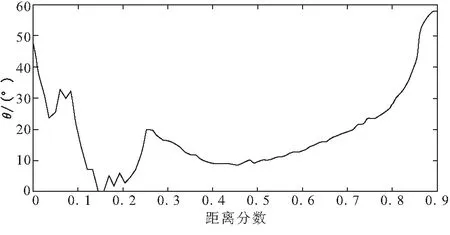
图12 界面法截面内主应力合力方向与界面法线夹角θ沿发动机长度方向分布

根据Mises应力及主应力计算出的界面附近推进剂损伤增加速率vD-Mises和vD-principal如图13(a)、(b)所示。由于时温等效作用，二者均在第5 200 h左右(7月份)达到最大值，vD-principal在6～8月份约为vD-Mises的2倍。

图14给出了1年后该层推进剂根据Mises应力及主应力计算出的累积损伤DMises和Dprincipal值分布。总体上，根据主应力计算出的损伤值大于根据Mises应力计算出的损伤值，尤其在发动机头部及尾部人工脱粘起始位置，由于法截面内主应力合力与界面夹角较小，导致在这两处位置的累积损伤计算值较大。

(a)Mises应力损伤速率vD-Mises

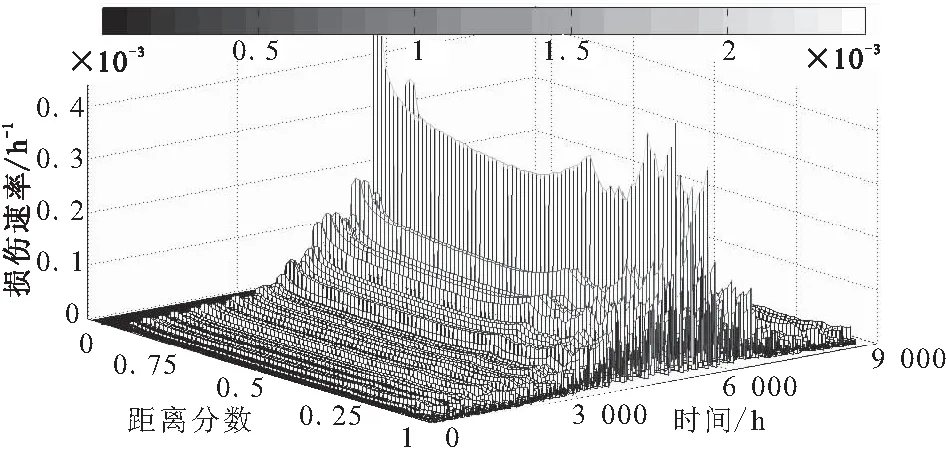
(b)主应力损伤速率vD-principal

(a)Mises应力损伤DMises

(b)主应力损伤Dprincipal

3 结论

(1)在多角度定载试验中，试件断裂过程分为2个阶段，首先衬层附近的推进剂出现脱湿，然后形成宏观裂纹直至试件断裂。给出了近似描述试件承载时间lgt随试件平均应力σ和载荷角度θ变化规律的线性模型。

(2)给出了发动机随1年环境温度变化所产生的界面损伤分布情况，根据主应力方向分析出界面各部位的累积损伤比采用Mises应力计算出的损伤高出50%左右。

(3)有限元计算给出的发动机界面附近主应力合力方向与界面并不垂直，发动机头部与尾部人工脱粘层根部的载荷角度θ较高，分别达到了50°和60°，而发动机圆柱段与头部圆弧段连接部位的载荷角度也达到了20°，并导致这3个部位的损伤计算值高于其他部位，这是发动机制造与使用过程中需要关注的部位。

参考文献：

[1] James Fillerup,Robert Pritchard. Service life prediction technology program[R].ADA 397950,1998.

[2] 冯志刚,方昌华,李静.国外导弹加速老化试验现状分析[J].飞航导弹,2007,5:47-52.

[3] Y1ld1r1m H C,ÖzÜpek S.Structural assessment of a solid propellant rocket motor:effects of aging and damage[J].Aerospace Science and Technology,2011,15:635-641.

[4] Heller R A,Singh M P,Zibdeh H.Environmental effects on cumulative damage in rocket motors[J].Journal of Spacecraft,1985,22(2):149-155.

[6] 孟红磊,赵秀超,鞠玉涛,等. 基于累积损伤的双基推进剂强度准则及试验[J].推进技术,2011,32(1):109-112.

[7] Richard K Kunz.Continuum damage mechanics modeling of solid propellant[R].AIAA 2008-4973.

[8] Richard K Kunz.Characterization of solid propellant for linear cumulative damage modeling[R].AIAA 2009-5257.

[9] Robert E Benton,Jr.Double-linear cumulative-damage reliability method[R].ADA 545867,2011.

[10] 邓斌,杨东,段静波.温度载荷下的药柱累积损伤分析[J].推进技术,2013,34(2):280-284.

[11] 郑晓亚,柳青,王卫祥.固体装药结构界面应力分析[J].航空动力学报,2012,27(8):1861-1865.

[12] Christiansen A G,Laheru K L,Anderson G P.Cohesive and adhesive analog test specimens for solid propellant grain simulation[R].AIAA 1983-1118.

[13] Kuhlmann T L,Peeters R L and Bills K W,et al.Modified maximum principal stress failure criterion applied to propellant-liner bond failures[R].AIAA 1985-1439.

[14] Kuhlmann T L,Peeters R L,Bills K W,et al.Modified maximum principal stress criterion for propellant liner bond failures[J].J.Propulsion,1987,3(3):235-240.

[15] Herb Chelner,Jim Buswell,Dan Evans.Embedded sensors for monitoring solid propellant grains[R].AIAA 2005-4362.

[16] 何平笙. 高聚物的力学性能[M].合肥:中国科学技术大学出版社,2008.