自由装填药柱冷流冲击过程中流固耦合数值分析①
2014-03-15桂晓波蔡文祥
桂晓波,余 陵,蔡文祥,连 立
(1.南京理工大学 机械学院,南京 210094;2.淮海工业集团第三研究所,长治 046000)
0 引言
固体火箭发动机点火过程包含一系列复杂的物理化学反应,点火过程时间较短,但发生故障的概率却相对较高。自由装填药柱能够方便地更换装药,不存在粘结脱粘问题,大大延长了武器系统的存贮时间,因此得到广泛应用。发动机点火过程中自由装填药柱受到瞬态高压燃气压力作用发生变形,药柱结构完整性容易受到破坏,这是典型的流固耦合现象。近10年来,国内外逐步采用计算模拟手段对流固耦合现象进行分析。例如,John Montesano[1]提出了一种简化的单向流固耦合计算模型;曹琪等人[2-3]进行了贴壁浇注药柱的流固耦合模拟。目前,国内很少有人对自由装填药柱点火过程中的应力应变状态进行分析,自由装填药柱内孔和外环同时受到压力作用,且压力变化和分布各不相同,对此进行研究,有助于了解发动机故障发生的内在原因,并为发动机结构设计、装药设计和材料选择提供依据。冷流冲击实验主要利用高压气体模拟固体火箭发动机点火压强峰值,作为极限载荷作用在药柱上,对其进行流动冲击,为冲击载荷条件下药柱结构完整性的研究提供实验条件,为数值分析提供验证数据。
本文利用System Coupling耦合器作为流体计算软件FLUENT和结构分析软件ANSYS的数据交换平台,针对大长径比的自由装填药柱固体火箭发动机点火瞬态过程展开研究,对冷流冲击过程高压气体流动和推进剂药柱变形之间的相互作用进行了数值仿真,得到高压气体在火箭发动机内的流动状况,以及药柱在压力冲击下的应力与变形的变化规律,从而分析出容易失效的位置。
1 流固耦合数学物理模型
1.1 物理模型
冷流冲击模拟固体火箭发动机点火过程实验台主要由高压气体暂存式储气罐、过渡体及实验发动机等部分组成,根据实验装置建立的物理模型如图1所示,采用三维1/4对称模型。

图1 流固耦合物理模型示意图
为简化模型,不考虑壳体、衬层和绝热层。发动机总长914 mm,直径90 mm,长径比>10,属于大长径比发动机范畴。储气罐内径96 mm,计算时选取长度200 mm。
1.2 流场计算模型
流场区域进行分区建模,将气源、过渡体、燃烧室、喷管等分成12个分区,使用Workbench Mesh前处理软件对其进行网格划分,采用六面体占主体,生成对象如图2所示,共有单元219 041个,节点190 065个。
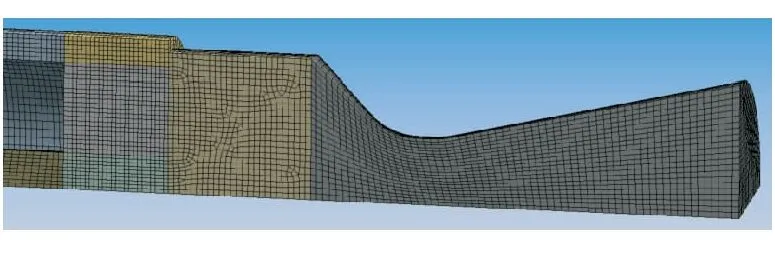
(a)前段网格

(b)后段网格
1.2.1 边界条件及初始条件
(1)储气罐设置为5 MPa压力气源;
(2)喷管出口压强为1个大气压;
(3)1/4对称面设置为周期性对称边界;
(4)装药头部、外壁、内壁为耦合边界。
计算模型的初始条件:p=0.101 325 MPa,T=295 K,速度为0,湍流动能k和动能耗散率ε取小值。
1.2.2 流场计算控制方程和计算方法
三维气相湍流流动守恒方程组包括连续性方程、动量方程和RNGk-ε方程,可表达成通用形式:
(1)
式中Φ为气相通用变量,在连续性方程中取1,在动量方程中表示u、v、w3个方向的速度,在RNGk-ε湍流模型中表示湍动能k和耗散率ε;S表示源项;Γ为扩散系数。
控制方程:
(2)
(3)
式中Gk表示由于平均速度梯度引起的湍动能产生;Gb表示由于浮力影响引起的湍动能产生;YM表示可压缩湍流脉动膨胀对总的耗散率的影响;αk和αε分别为湍动能k和耗散率ε的有效湍流普朗特数的倒数;C1ε、C2ε、C3ε为常数。
湍流粘性系数计算公式为
(4)

流场计算选用SIMPLE算法,RNGk-ε模型,时间步长为10-5s。
1.3 结构场计算模型
固体推进剂药柱为前后不对称的单孔管状装药,药柱后段外通道沿装药轴线方向减小,尺寸见表1。结构场模型网格划分采用六面体结构化网格,整个药柱生成单元19 800个,节点92 778个,见图3。

表1 装药结构参数

图3 药柱网格示意图
1.3.1 材料特性
固体推进剂药柱是一种典型的时间温度相关的粘弹性材料,在较低应力作用下近似线性粘弹性,其泊松比接近0.5,与不可压缩材料较为相似。这里采用线性粘弹性本构模型,基本可满足工程的需要,其拉压松弛模量可用Prony级数表示[4]:
其中,泊松比为0.495;瞬态弹性模量为2 671.2 MPa;密度为1 775 kg/m3。
1.3.2 计算方法
瞬态动力学分析求解的基本运动方程为
[M]{u″}+[C]{u′}+[k]{u}={F(t)}
(5)
式中 [M]表示质量矩阵;[C]表示阻尼矩阵;[k]表示刚度矩阵; {u″}表示节点加速度向量; {u′}表示节点速度向量; {u}表示节点位移向量; {F(t)}表示t时刻的载荷向量。
计算时,将药柱后端面约束固定,前端面、外壁面和内壁面为流固耦合面,两个对称面;采用Newton-Raphson法求解,时间步长与流场迭代步相同;每次迭代步计算后,利用System Coupling耦合器在FLUENT和ANSYS之间进行数据交换。
1.4 流固耦合方法
本文数值模型,推进剂具有较大的长径比,在发动机点火流场建立过程中,推进剂装药结构场变形很小,从整个发动机燃烧室尺度出发,可认为固体域的变形对流体域的影响可忽略不计,而流场的建立对结构分析有重大影响,故在研究中,流固耦合分析采用单向耦合分析法,仅考虑冷流冲击流场对装药结构的影响。在冲击瞬间,冷流气体升温幅度并不大,可认为药柱处于常温下,不涉及粘弹性材料随温度变化关系,只研究药柱在峰值压力作用下随时间变化的受力情况。
System Coupling作为ANSYS workbench解决流固耦合问题的求解器,可按照设定的顺序在FLUENT和ANSYS中分别进行流体计算和固体计算,通过流固耦合面(FSI Interface)把流体域和固体域的计算结果相互交换传递。待某一时刻的流固计算均达到收敛要求,进行下一时刻的计算,依次而行求解得到随时间变化的流场及结构场的变化过程。具体计算流程[5]如图4所示。
2 计算结果及分析
通过仿真计算可知,在0.35 ms时,流场压力前锋抵达药柱前端面,流场开始对药柱产生作用力。图5(a)为0.35 ms时刻的流场速度马赫数云图,高压气体进入燃烧室,在药柱前端面扩展区形成高度欠膨胀超声速射流[6],进入内通道形成高速流区。图5(b)为1.15 ms时刻内通道气流进入后腔形成约束管内的射流波系结构,内通道气流压力波传递快于外通道,当内通道压力波前锋到达后端面时,外通道压力前锋还没有到达,此时的内外通道压力差导致装药呈内壁膨胀状态。图5(c)为1.40 ms时刻内外通道气流在后腔相遇,此时波系混乱,后腔内流场状况非常复杂。

图4 流固耦合流程示意图
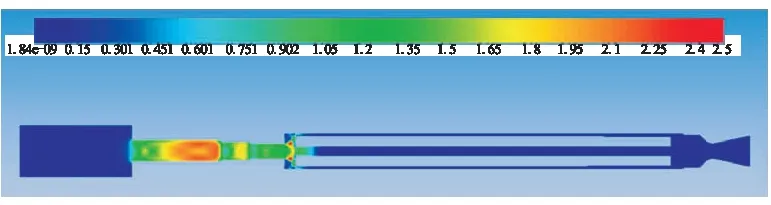
(a)0.35 ms

(b)1.15 ms
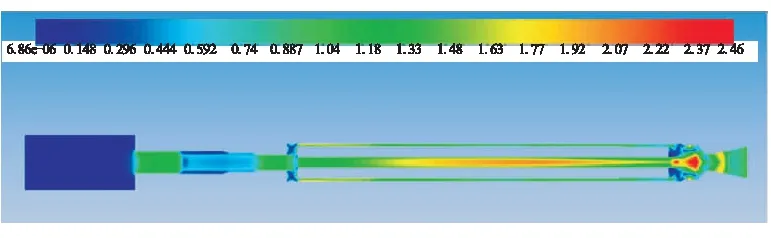
(c)1.40 ms
经过耦合传递,流场压强作用在药柱推进剂上,产生应力和变形。图6为0.35 ms时刻药柱应力与变形分布图。此时流场压力前锋刚进入药柱内通道,正面轴向冲击使前端面内孔边缘出现最大变形,变形量为0.005 7 mm,这一阶段变形较小。最大应力出现在内孔离前端面距离5 mm左右的内壁面,这主要是因为轴向压力对前端面的挤压,应力值为0.657 3 MPa。

(a)应力分布

(b)变形分布
图7为1 ms时刻药柱应力与变形云图。这时,左端药柱头部内壁应力4.119 9 MPa,底部外壁边缘,也就是后挡药板爪卡固定处,应力达4.119 6 MPa,如图7(a)所示。由于压力波的传递及内外压力差作用,药柱最大应力位置随之转移至药柱底部外壁边缘。这时的药柱头部最大变形量为0.390 49 mm。从图7(b)可知,药柱变形主要为头部冷流冲击所导致的轴向变形。

(a)应力分布

(b)变形分布
图8为药柱最大变形量随时间变化曲线,呈震荡变化趋势,在1.73 ms时,变形量上升到最大值,为1.078 5 mm,位置在药柱头部端面。由于粘弹性材料弹性,最大变形量呈震荡变化,弹性模量决定了最大变形的大小。随正面冲击的冷流气体压力下降,震荡幅度也逐渐减小,变形量也随之减小。
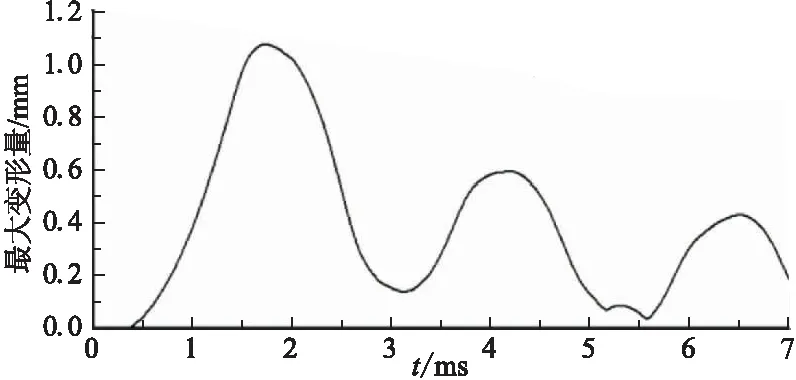
图8 最大变形量随时间变化曲线
图9给出药柱最大应力和底部外壁边缘应力随时间变化曲线。底部外壁边缘应力呈震荡变化,同样是粘弹性材料弹性特性的体现。两者重合部分即最大应力由头部转移至底部时刻。1.91 ms时,药柱底部外壁边缘的应力最大,其值为13.32 MPa,最大应变0.005 115 5(见图10,左端为底部)。因此,整个冲击过程中,底部外壁边缘和头部内壁最易发生结构完整性破坏,在结构设计和材料选择上应加以重视。
实验过程中,在药柱头部外壁、头部内壁、头部正面及底部外壁等5处粘贴电阻应变片,进行多次测量,得到的应变数据也反映了在头部内壁和底部外壁处的应变要比其他所有监测点大,从而验证了数值分析的正确性。药柱的失效准则一般采用八面体剪切理论[7],其失效函数为
(6)
式中γ8m为八面体剪应变的极限值;μ为泊松比;εe为最大等效应变;εM为药柱单向拉伸的最大延伸率,可由实验得到。
文中使用的药柱延伸率为35%,远大于最大等效应变,Z′>0。因此,药柱没有发生失效。
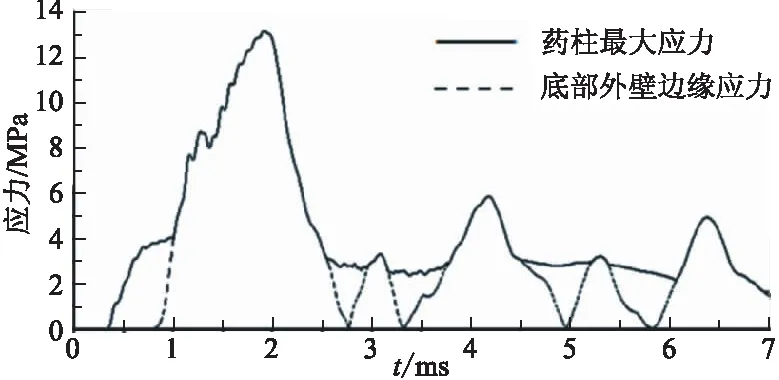
图9 药柱最大应力和底部外壁边缘应力随时间变化曲线

(a)应力分布

(b)应变分布
3 结论
(1)仿真结果表明System Coupling耦合器能够很好的将FLUENT和ANSYS结合进行耦合计算,同时同步计算流场和结构场,更能准确模拟冷流冲击实验过程的实际工作状况。
(2)药柱变形沿轴向逐渐减小,材料的弹性特性使最大变形量随时间呈震荡变化,瞬态弹性模量决定最大变形的大小。
(3)在压力上升及传播过程中,自由装填药柱头部内孔壁及底部外壁边缘Mise应力较大,最大应力在这2个位置交替变化,这与实验测得的数据相一致。
(4)在点火压力峰值阶段,最大Mise应变产生在底部外壁边缘,易造成药柱结构完整性破坏。因此,对此处的结构设计和力学性能要求较高。
参考文献:
[1] John Montesano,Kamran Behdinan,David R Greatrix,et al.Internal chamber modeling of a solid rocket motor: effects of coupled structural and acoustic oscillations on combustion[J].Journal of Sound and Vibration,2008,311: 20-38.
[2] 曹琪,李进贤,唐金兰.带径向翼槽SRM点火瞬间流固耦合数值分析[J].固体火箭技术,2009,26(12).
[3] 高双武.含缺陷固体火箭发动机点火瞬态流固耦合数值模拟[D].西安高科技研究所,2007.
[4] 曹杰.自由装填固体火箭发动机装药点火冲击特性研究[D].南京理工大学,2013.
[5] 崔小强.激波与固体火箭发动机装药裂纹流固耦合基理研究[D].国防科学技术大学,2007.
[6] Purcell Steven P,Daines Weldon L,Christensen Leon W.Simulation of the pressure gradient in a segmented solid rocket motor during the ignition transient[C]//Joint Propulsion Conference and Exhibit,1992: 24.
[7] 张书俊.固体火箭发动机粘弹性药柱结构可靠性分析[J].固体火箭技术,2006,29(3).
