平底翼柱型药柱燃烧规律的研究①
2019-03-27刘瑞东相升海杨艳羽
刘瑞东,相升海,杨艳羽,于 兵,杨 丽
(沈阳理工大学 装备工程学院,沈阳 110159)
0 引言
固体火箭发动机装药的几何形状和尺寸决定了燃烧面积变化规律[1]。药柱按照燃烧方向可分为三大类,即一维药柱(端燃药柱)、二维药柱(侧燃药柱)和三维药柱(侧端燃药柱)。翼柱型药柱是一种三维药柱,它靠圆柱部分提高体积装填系数,靠“翼”来调节燃面变化,具有装填系数高、燃面可调范围大的优点[2]。按照封头类型的不同,翼柱型药柱又可分为平底型、碟型、椭球型与半球型。文献[3]给出了翼槽数为15时的燃烧规律。文献[4]研究了温度载荷下翼柱型装药的受载响应。文献[5]给出了一种三维药柱燃烧过程分析方法。文献[6]给出了一种三维径向开槽药柱的设计方法。文献[7]给出了开槽管型药柱的燃烧规律。文献[8]给出了翼柱型装药发动机工作过程中声腔振动频率与药柱不稳定燃烧现象的关系。文献[9]给出了一端开翼槽,翼槽数为13的翼柱型药柱设计方法。文献[10]分析了4种不同药柱的减面性。文献[11]给出了后翼柱型装药的设计方法。文献[12]研究了发动机装药燃面数值计算方法。文献[13]给出了两端开翼槽的翼柱型药柱推力曲线。文献[14]研究了一端开翼槽的翼柱型药柱内弹道性能。文献[15]研究了发动机燃烧过程中激波的传播规律。本文主要对中间开翼槽且翼槽数为8的平底翼柱型药柱燃烧规律进行研究。
1 几何模型
如图1所示,平底翼柱型药柱的设计参数主要有:药柱外径D,药柱内径d,药长L,后圆柱段药长L1,前圆柱段药长L2,翼槽倾角α、β,翼顶缘半径r,槽深H,翼槽厚度2T,翼数N。由于所开翼槽具有对称性,因此选择其中一个槽作为研究对象。文中角度均为弧度制,与长度有关设计参数以外径为基准进行无量纲化。
此外,本次研究中采用平行层燃烧定律,它基于以下假设:
(1)整个装药的燃烧表面同时点燃;
(2)装药成分均匀,燃烧表面各点的条件相同;
(3)燃烧表面上各点都以相同的燃速向装药内部推移。

(b)翼柱型药柱三维模型及燃面划分示意图
2 药柱燃烧规律
2.1 燃面计算
将翼柱型药柱外侧面及一侧端面包覆,将其划分为11个燃烧面,推导得出各个燃面的面积计算公式,燃烧面的划分见图1(b)。
(1)后圆柱段燃烧面
(1)
(2)前圆柱段燃烧面
(2)
(3)中间圆柱段燃烧面
(3)

(4)侧端面
(4)
(5)翼槽左侧平面
(5)
(6)翼槽右侧平面
(6)
(7)翼顶缘面
S7=(α+β)(r+e)T
(7)
(8)翼槽底面
(8)

(9)翼槽左侧圆柱面
(9)
(10)翼槽右侧圆柱面
(10)
(11)翼顶缘与翼槽底面相连圆弧面
S11=(α+β)×e2
(11)
2.2 燃烧过程中关键点的确定
药柱燃烧过程中关键点的位置如图1(a)所示。关键点的计算公式如下:
(1)翼槽相连点e1
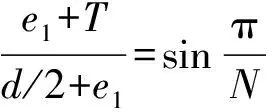
(12)
(2)翼槽底面燃尽点e2
(13)
(3)翼顶缘与药柱外侧面相连点e3
e3=(D-d)/2-H
(14)
(4)侧端面燃尽点e4
(15)
(5)翼顶缘燃尽点e5
(16)
(6)药柱燃尽点e6
e6=(D-d)/2
(17)
2.3 约束条件
为尽可能减少残药,令前圆柱段、后圆柱段同时消失,且此时翼顶缘恰好与药柱外侧面相连,可得到约束条件:
则
L1=λ·[1+tan(α/2)]
(18)
则
L2=λ·tan(β/2)
(19)
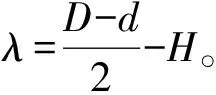
2.4 燃烧面积变化规律
Q2·tan2θ+2(α+β)π]·e+
(π/N-φ)·L+φ·L1+
φ·L2+Q1·T+
[Q2·tanθ-Q3·tanθ+
π(cotα+cotβ)/2-Q3/2]·r+
(Q3·π/2-Q2·tanθ)·H-
(πd/N+φ·Q1·d/2)
(20)
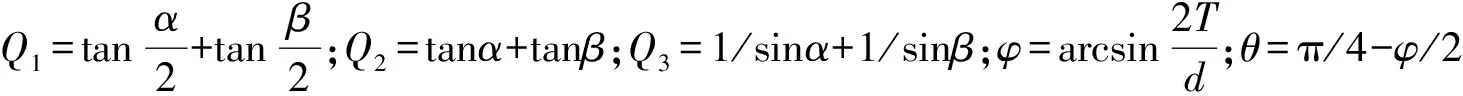
令
Q2·tan2θ+2(α+β)π
B1=π/N-φ
B2=φ
B3=Q1
B4=Q2·tanθ-Q3·tanθ+
π(cotα+cotβ)/2-Q3/2
B5=Q3·π/2-Q2·tanθ
B6=-(πd/N+φ·Q2·d/2)
则有
B3T+B4r+B5H+B6
(21)
(1)恒面燃烧条件
要使药柱燃烧过程呈现恒面性,则需df(e)/de=0,即A≡0,B1L+B2L1+B2L2+B3T+B4r+B5H+B6=0,求解可得:N≈-5.021 7。由于开槽数N一定是正整数,得到的N不满足要求,因此平底翼柱型药柱燃烧过程不具有恒面性。
(2)翼槽数的选择
燃面变化率df(e)/de与翼槽数N的关系如图2所示。其中,网格面代表df(e)/de=0。
从图2可看出,当翼槽数N≤8时,药柱燃烧过程呈现先增面后减面的特性,且翼槽数越少,增面性越强;当翼槽数N≥9时,药柱燃烧过程呈现单增面性。因此,下面将研究翼槽数≤8时药柱燃烧面积的变化规律。
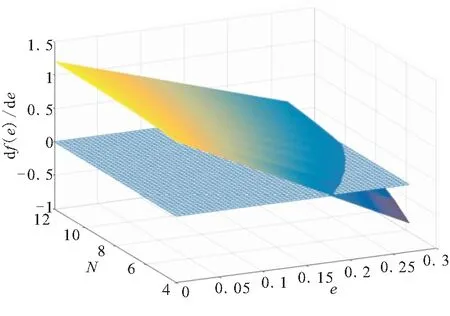
图2 df(e)/de与N的关系Fig.2 Relationship between df(e)/de and N
图3给出了翼槽数分别为4~8时药柱的燃烧面积曲线图。从图3中可看出,翼槽数为8时,燃烧过程更接近恒面性。因此,将选取翼槽数N=8的药柱进一步研究其燃烧规律。
(3)翼槽倾角对燃烧面积的影响
燃面变化率df(e)/de与翼槽倾角α、β的关系如图4所示。其中,网格面代表df(e)/de=0。
从图4可看出,当α(0,5π/48),β(0,π/3)时,药柱燃烧过程呈现先增面后减面的特性,且随着α、β的增大,变化过程趋于平缓。因此,在研究中,翼槽倾角选取接近其区间上限的适当值。其中,α取π/12,β取11π/36。
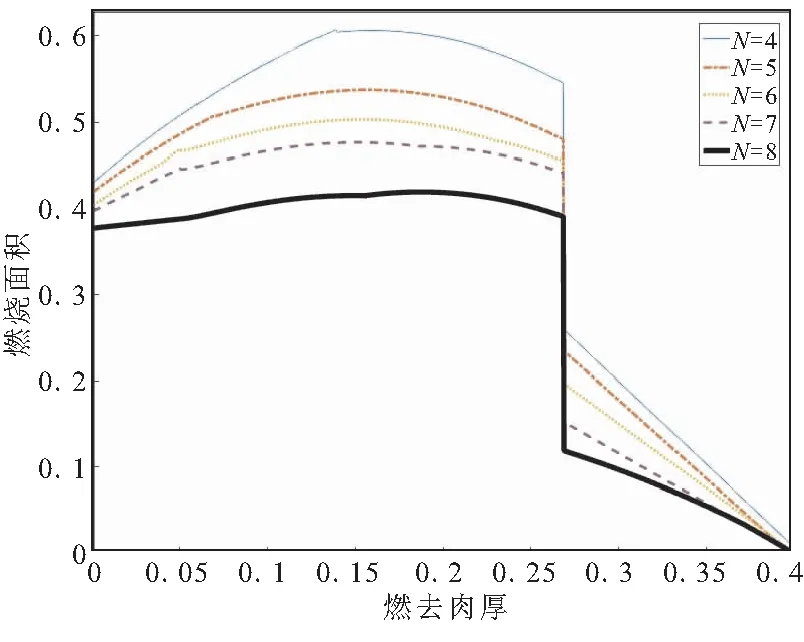
图3 翼槽数对燃烧面积的影响Fig.3 Effect of burning area in different number of fins

(a)df(e)/de与α的关系
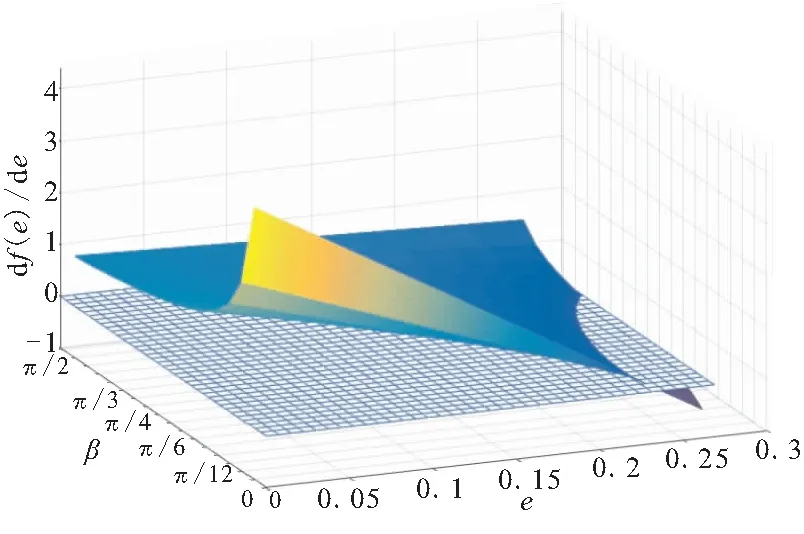
(b)df(e)/de与β的关系
(4)敏感度分析
当翼槽倾角α=π/12,β=11π/36,N=8时,设计变量d、L、r、H、T对燃面变化率df(e)/de的影响如图5所示。
由图5可知,对燃面变化最敏感的设计变量为H、r、T。因此,在2.4节(6)中,将重点研究df(e)/de与H、r、T的变化关系。
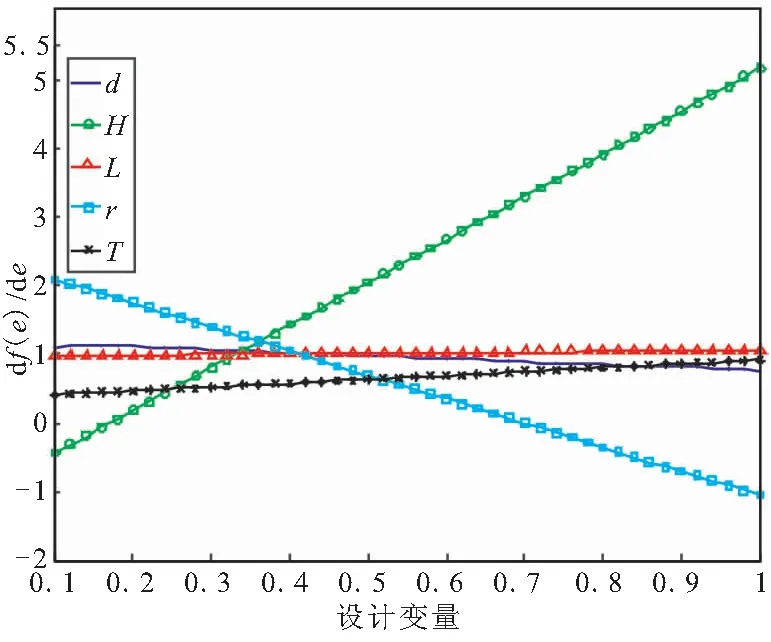
图5 燃面变化率df(e)/de与设计变量的关系图Fig.5 Relationship between df(e)/de and parameters
(5)长径比对燃烧面积的影响
由式(18)和式(19)可看出,药柱前圆柱段长L2与后圆柱段长L1只受到外径D、内径d以及翼槽深度H的影响。因此,长径比L只对中间圆柱段消失前的第一阶段燃烧面积有影响。图6给出了5组不同长径比L所对应的药柱第一阶段燃烧面积曲线图。从图6中可看出,当长径比为1.7时,药柱初期燃烧最接近恒面燃烧。因此,选取长径比为1.7的药柱进一步研究其燃烧规律。

图6 长径比对燃烧面积的影响图Fig.6 Effect of burning area in different aspect ratio
(6)燃面变化率与设计变量的关系
当d=0.2,L=1.7,N=8时,联立式(18)、式(19)和式(21),可得到燃面变化率df(e)/de与设计变量r、H、T的关系图,如图7所示。图7中,网格面代表df(e)/de=0。
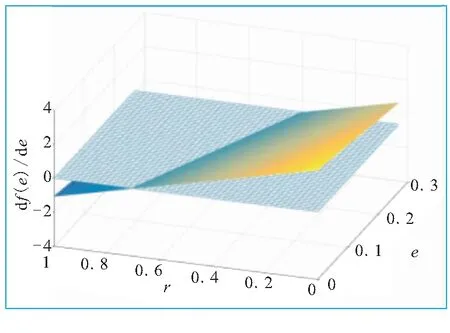
(a)df(e)/de与r的关系
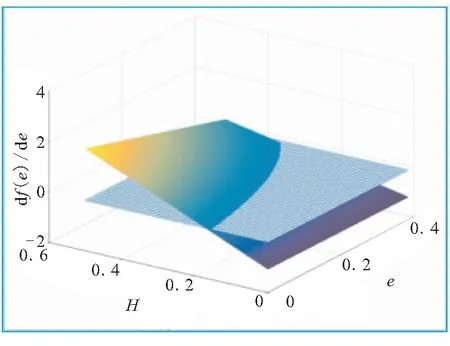
(b)df(e)/de与H的关系

(c)df(e)/de与T的关系
由图7可知:
当0 当0 当0 选取平底翼柱型药柱设计参数为药柱外径D=500 mm,药柱内径d=100 mm,药长L=850 mm,翼槽倾角 ,翼顶缘半径r=190 mm,槽深H=175 mm,翼槽厚度2T=30 mm,翼数N=8。 使用UG三维建模软件对所研究药柱建立三维模型,提取5个关键点的燃烧面积,并与推导燃面公式计算值进行比较,如表1所示。其中,最大相对误差为0.21%,由此可知本文的公式是正确的。 表1 燃面数据对比 以药柱外径为基准,将设计参数进行无量纲化,可得d=0.2,L=1.7,H=0.35,r=0.38,T=0.03。根据图7,药柱燃烧过程应为先增面、后减面燃烧。 根据式(1)~式(11),得到燃烧面积变化曲线,如图8所示。燃烧过程呈现先增面性、后减面性,与所得规律相吻合。 图8 燃烧面积变化曲线Fig.8 Curve of the burning area (1)当翼槽倾角α∈(0,5π/48),β∈(0,π/3)时,药柱燃烧过程呈现先增面、性后减面性。 (2)以药柱外径为基准,当设计参数翼顶缘相对半径r∈(0.36,0.71),翼槽相对深度H∈(0.17,0.375),开槽相对厚度T∈(0,0.036),药柱呈现先增面、后减面燃烧;当设计参数r、H、T在给定范围外时,药柱燃烧呈单增面性,或者单减面性。 (3)翼槽数为8,长径比为1.7时,燃烧过程更接近恒面。 (4)平底翼柱型药柱不存在恒面燃烧。3 算例


4 结论
