正五边形港湾内的水波共振
2014-03-14郑金海董文凯徐龙辉
郑金海,董文凯,徐龙辉,3,王 岗
(1.河海大学海岸灾害及防护教育部重点实验室,江苏南京 210098; 2.河海大学港口海岸与近海工程学院,江苏南京 210098;3.苏州市航道管理处,江苏苏州 215002)
当外海波浪传入港内时,若其频率与港湾的共振频率接近或一致,港内水面会出现剧烈振荡,这种现象称之为港湾共振。港湾共振可以导致港内船舶剧烈晃动、碰撞,甚至断缆,使港内无法正常装卸作业[1]。
港湾共振频率与港口的几何形状、平面布置、港内水深及海底地形等因素有关。针对不同几何形状的港湾,国内外学者做了大量研究。Miles等[2]基于以格林函数为基础的积分方程得到狭长矩形港湾的共振条件和放大因子的解析解。Ippen等[3]应用傅里叶变换法,在口门处匹配波面和流速条件,得到了矩形港湾共振问题的解析解。Le Mehaute等[4]计算单一周期波浪作用下变水深矩形港口的共振周期解析表达式。Wang等[5-6]考虑了水深对波浪共振的影响并详细推导了内部地形为斜坡的矩形港湾内共振的解析表达式,首次提出变水深港湾内存在类似于边缘驻波的横向共振,并通过数值模拟验证了这一推断。郑金海等[7]针对具有斜坡的矩形港湾做了进一步研究,指出斜坡底床港湾内纵向共振的本征频率比常水深小,而共振幅度受波浪浅化作用的影响明显增大。这些研究大多分析形状规则的港湾共振问题,虽然很少能直接应用于实际工程中,但是他们对认识港湾共振机理有重要意义。
经典Boussinesq方程是Peregrine[8]从Euler方程出发,引入非线性项和色散项,采用摄动法推导而来,它的弱非线性和弱色散性限制了方程的适用范围和计算精度。Witing[9]、Madsen等[10-11]、Nwogu[12]和Ge等[13]通过加入高阶偏微分项或者调节水层位置提高了方程的色散性和非线性,使其成为描述波浪在近岸水域传播变形的理想模型[14]。史宏达等[15]在理想地形条件下,应用MIKE21-BW模块模拟了矩形港湾的港内共振。马小舟等[16]采用文献[15]中的模型,计算了不同波高的孤立波分别在常水深和变水深狭长港内传播时的波高分布。
港口的几何形状是影响港湾共振的一个重要因素,人们试图找到一种特定形状的港池可以削弱甚至避免港湾共振。正五边形是一种规则、常见的几何形状,但是其内水波运动的理论分析还未有相关文献涉及。主要原因是其边界比较复杂,无法用传统的方式进行求解,因此有必要针对五边形港池进行水波运动分析,了解其内的港湾共振机理。港湾共振通常发生在近岸,且共振频率对应的波长远大于港湾的水深,可以认为是浅水波浪问题。因此,笔者基于一维驻波形成机理,分析常水深正五边形港湾内的水波运动形式,并采用Boussinesq模型进行模拟验证,分析各模态的共振特征。
1 理论分析
波浪在港湾内传播,遇到直立壁面会发生完全反射,反射波与入射波叠加形成驻波。图1揭示了正五边形港湾内由驻波产生共振的机理。垂直壁面a的波浪倾斜射向直立壁面b,并在b处完全反射。反射波继续传播,进而垂直射向壁面c,在壁面c处发生反射后按原来路线返回。波浪在壁面a、b、c之间往复运动,反射波浪与入射波浪之间相互作用形成驻波。这种驻波虽然在形式上比一维港湾复杂,但其产生机理完全一致。此时,壁面a与壁面c之间的距离相当于一维港湾的几何长度,称为产生共振的特征长度。由几何关系得特征长度为

图1 正五边形港湾共振机理Fig.1 Resonance mechanism of regular pentagon-shaped harbor
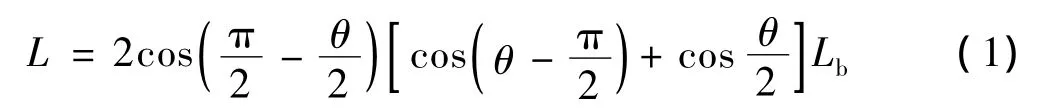
式中:Lb——正五边形边长;θ——正五边形内角,θ=0.6π。
对于水深为h的封闭港湾,任意波向第n模态共振的本征波数应满足:

由于笔者采用Boussinesq模型进行模拟,为了模拟结果与理论分析的统一,同样采用二阶Boussinesq方程的频散关系得其对应的角频率ωn为

波数kn与波长λn的关系式为

由式(4)和频散关系得不同共振频率对应的引起共振的波长:

由式(2)和式(5)可知波浪在正五边形港湾内发生共振时,n满足:

2 正五边形水波数值模拟
2.1 数值模型
由海底地震引起的海啸模拟通常可以将水底的变形直接等效为相应的水面变化,因此模拟凸出水面引起的扰动可以视为底床运动激发的水面波动现象。笔者运用Wang等[6]建立的基于二阶色散性Boussinesq模型进行研究。
如图2所示,正五边形港湾边长4m,水深恒为0.5m。港湾中心处、面积为其1/10的正五边形区域高出静止水位0.025 m。模型模拟该凸出水面在重力作用下引起港内的自由水面波动过程。计算网格为128×133,时间步长为0.01 s,模拟时间为250 s,以确保整个区域内的自由水面波动达到稳定。港湾壁面为全反射边界。
为分析港内不同位置的共振特点,取3个测点:P1为港湾边界中心;P2为港湾拐角处;P3为港湾中心处(图2)。

图2 正五边形港湾平面布置(单位:m)Fig.2 Plan sketch of regular pentagon-shaped harbor(units:m)
2.2 结果分析
笔者主要研究小幅度运动引起的正五边形港湾内的共振现象,港内自由水面在达到稳定状态后各共振模态的波幅与水深相比很小,即港内水波运动的非线性很小,可以认为各个共振模态是独立存在的,在稳定状态,他们之间的能量传递可以忽略不计。
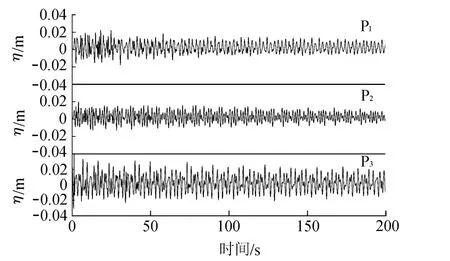
图3 正五边形港湾内P1、P2和P3的波面过程线Fig.3 Time histories of wave surface at P1,P2,and P3of regular pentagon-shaped harbor

图4 正五边形港湾内最大波高分布Fig.4 Distribution of maximum wave height within regular pentagon-shaped harbor
图3为正五边形港湾内3个观测点的波面变化过程线,其中纵轴为自由波面(η)。P1、P2初始水面为零,随后受到来自港湾中央初始水面产生的波动影响,开始运动。初始时刻波幅值较大,且相对杂乱;进入稳态后波幅值较小且相对稳定。P3初始水面为0.025 m并迅速下降至-0.03 m,随后又迅速上升达到正的最大位移。进入稳态后,P3点的波幅值明显大于P1、P2点。各点运动大约在t=60 s时达到平稳状态。
图4为共振平稳后港内最大波高的分布图。正五边形港内波高呈明显的几何中心对称;围绕港湾中心位置存在明显的波节线;港湾边界处波高值较大;最大值出现在港湾中央。
取时间段为86.17~250.01 s的波面过程进行傅里叶变换,得其波幅谱如图5所示。正五边形港湾中央P1点,主要共振频率值为0.214Hz、0.421Hz、0.519Hz、0.592Hz及0.659Hz;不同频率对应的波幅值近似相等,都在0.002 m以下。P2主要共振频率值与P1基本一致,但频率值0.421 Hz与0.519 Hz对应的波幅值较大。P3点共振频率值数量较少,只有0.421 Hz具有较大波幅值。
对于正五边形港湾模态n的确定采用如下原则:由各共振频率模拟值fn代入式(5)得到对应波长λn,进一步代入式(6)确定模态数n;由式(2)确定第n模态共振频率理论值ft。将波幅谱中各共振频率模拟值与计算得到的正五边形港湾内共振频率的理论值进行比较,并计算其相对误差列于表1。
由表1可知,模拟结果与理论分析吻合良好,表明上述理论推导可以正确地解释正五边形港湾共振的激发原理。因此封闭正五边形港湾内主要体现为类似一维港湾的单一波向上的共振,而产生共振的主要原因是壁面之间形成驻波的叠加结果。
在正五边形港湾内部均匀取点,将各点波面过程线做傅里叶变换得到各共振模态对应的波幅谱,结合各点坐标得到各共振模态所对应的波幅分布(图6)。

图5 正五边形港湾内P1、P2和P3对应的波幅谱Fig.5 Amplitude spectra at P1,P2,and P3of regular pentagon-shaped harbor

表1 正五边形港内各共振模态对应模拟结果与理论值的比较Table 1 Comparison of simulation results and theoretical values of oscillation models within regular pentagon-shaped harbor
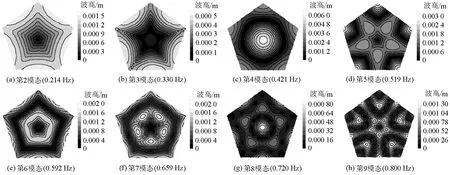
图6 正五边形港湾内各共振模态波高分布Fig.6 Distribution of wave height of all oscillation models within regular pentagon-shaped harbor
正五边形港内,各共振模态波高分布均呈现明显的中心对称。第4模态(即fn=0.421 Hz)是港内产生水波共振的主要模态,其对应的波高值最大,占有大部分能量,这与图5反映的现象一致。第5~6模态次之,波幅值较大。当n取值较大时,对应波幅忽略不计。
第2模态与第3模态波高分布整体类似。港湾中央波高值最小,边界处由于法相速度为零,波幅值较大,最大值在边界中点处。
第4模态与其他共振模态相比区别较大。港湾中央波高值最大,并向外逐渐减小,形成一圈波节线。港湾拐角处出现波高极大值,各边中心处为波节点。
第5模态出现更多的波峰及波节点。港湾中央波高值最小,中心周围出现5个较大波峰,最大波高出现在港湾拐角处,且围绕各拐角形成波节线。
第6模态与第7模态类似,围绕中央存在明显的波峰线和波节线。港湾中央波高最小,并向外逐渐增大;港湾边界处同样由于法相速度为零而波高值较大;边界与港内波峰线间形成波节线。两者不同的是,第6模态港内波峰线为封闭的整体,而第7模态是由5个较大的波峰连接而成;第6模态最大值出现在5条边的中心处,而第7模态最大值在每条边界有2处,分别为1/4和3/4处。
第8模态中心处波高最大,5个波峰围绕在其外。此外,5条边的中心处波高为极大值,5个顶点处为波节点。
第9模态港内波高分布更加复杂,出现多个波峰及多条波节线。港湾中央为波节点,其周围出现5个相连的波峰,且每个波峰与对应边界中央的波峰相连,形成波峰线。靠近拐角处也出现波高值较大的波峰,并垂直延伸至港湾边界。拐角处波幅值也比较大,相邻波峰间形成波节线,且围绕着港湾拐角分布。
总之,正五边形港湾各共振模态波高分布呈明显的中心对称。低模态的波高分布比较简单。但随着n增大,港湾内波节点和波峰线数量增加,分布变得更复杂。
3 结 语
通过理论分析和数值模拟相结合的方法研究了正五边形封闭港湾内的水波共振问题。首先,基于浅水长波假定,引入特征长度的概念,推导了正五边形封闭港湾内各共振模态的理论频率,并与数值模拟比较,验证理论分析的正确性;其次,在此基础上研究数值模拟中出现的各共振模态及能量分布,得到了正五边形港湾内各共振模态能量空间分布图。
[1]王岗,马小舟,马玉祥,等.短波对港湾长周期振荡的影响[J].工程力学,2010,27(4):240-245.(WANG Gang,MA Xiaozhou,MA Yuxiang,et al.Long-period harbor resonance induced by short waves[J].Engineering Mechanics,2010,27 (4):240-245.(in Chinese))
[2]MILES J,MUMK W.Harbor paradox[J].Journal of the Waterways and Harbors Division,1961,87:111-132.
[3]IPPEN A T,GODA Y.Wave induced oscillations in harbors:the solution for a rectangular harbor connected to the open-sea[R].Washington D C:Hydrodynamics Laboratory,Massachusettes Institute of Technology,1963.
[4]LE MEHAUTE B,KOH R.On the breaking of waves arriving at an angle to the shore[J].Journal of Hydraulic Research,1967,5(1):67-88.
[5]WANG G,DONG G,PERLIN M,et al.An analytic investigation of oscillations within a harbor of constant slope[J].Ocean Engineering,2011,38(2/3):479-486.
[6]WANG G,DONG G,PERLIN M,et al.Numerical investigation of oscillations within a harbor of constant slope induced by seafloor movements[J].Ocean Engineering,2011,38:2151-2161.
[7]郑金海,徐龙辉,王岗,等.斜坡底床港湾内横向与纵向波浪共振的解析解[J].工程力学,2013,30(5):293-297. (ZHENG Jinhai,XU Longhui,WANG Gang,et al.Theoretical analysis of transverse and longitudinal oscillations within a habor of constant slope[J].Engineering Mechanics,2013,30(5):293-297.(in Chinese))
[8]PEREGRINE D H.Long waves on a beach[J].Journal of Fluid Mechanics,1967,27(4):815-827.
[9]WITING J M.A unified model for the evolution of nonlinear water waves[J].Journal of Computational Physics,1984,56(2): 203-236.
[10]MADSEN P A,MURRAY R,SORENSEN O R.New form of the Boussinesq equations with improved linear dispersion characteristics[J].Coastal Engineering,1991,15(4):371-388.
[11]MADSEN P A,SORENSEN O R.A new form of the Boussinesq equations with improved linear dispersion characteristics.Part 2:a slowly-varying bathymetry[J].Coastal Engineering,1992,18(3/4):183-204.
[12]NWOGU O.Alternative form of the Boussinesq equations for nearshore wave propagation[J].Journal of Waterway,Port,Coastal,and Ocean Engineering,1993,119(6):618-638.
[13]GE Wei,KIRBY J T,STEPHAN T G,et al.A fully nonlinear Boussinesq model for surface waves.Part 1:Highly nonlinear unsteady waves[J].Journal of Fluid Mechanics,1995,294:71-92.
[14]马小舟,董国海,滕斌.破碎带波浪的数值模拟[J].计算力学学报,2007,24(2):203-208.(MA Xiaozhou,DONG Guohai,TENG Bing.Numerical modeling of waves in surf zone[J].Chinese Journal of Computational Mechanics,2007,24 (2):203-208.(in Chinese))
[15]史宏达,徐国栋,孙龙龙.矩形港湾的港内共振研究[J].海岸工程,2011,30(2):14-21.(SHI Hongda,XU Guodong,SUN Longlong.Study on resonance in a rectangular harbor basin[J].Coastal Engineering,2011,30(2):14-21.(in Chinese))
[16]马小舟,刘嫔,王岗,等.孤立波作用下细长港响应的数值研究[J].计算力学学报,2013,30(1):101-105.(MA Xiaozhou,LIU Ping,WANG Gang,et al.Numerical study on the response of a narrow-long harbor to a solitary wave[J]. Chinese Journal of Computational,2013,30(1):101-105.(in Chinese))
