基于改进粒子群算法的双馈感应发电机参数辨识

刘永康，潘学萍，鞠 平

(河海大学能源与电气学院，江苏南京 211100)

由于风能具有随机性、波动性等特点，风电接入给电力系统带来了新的安全稳定问题和运行调控问题［1］。要对含大规模风电的电力系统进行仿真与分析，合适的模型是关键。

目前风力发电机组在机理建模方面的研究已有较多的成果，辨识建模与模型验证方面的工作也在广泛展开［2-4］。辨识建模过程中，一般选择某变量为观测量，参数辨识的目标是寻找待辨识参数，使得仿真轨线与实测轨线间的误差达到最小，因此参数辨识的实质是优化问题。

合适的优化算法可提高参数的辨识精度。目前在电力系统参数辨识中，采用的优化算法主要有非线性最小二乘算法［5］、蚁群算法［6］、微变搜索算法［7］、卡尔曼滤波算法［8］、基因算法［9］、模拟淬火算法［10］等。

粒子群优化算法［11］具有全局性能好、收敛速度快等特点，在电力系统参数辨识及其他工程领域得到了广泛的应用。该算法的缺点为优化后期收敛速度慢，易陷入局部最优点。鉴于此，程颖等［12-13］通过改变粒子的惯性权重提高全局搜索能力和收敛精度;胡家声等［14-15］在基本PSO算法的基础上，采用更多粒子的位置值信息进行变异操作，并且提出根据各粒子的适应值大小确定算法控制参数的方法，保证了算法的收敛性。本文在对双馈风力发电机组进行参数辨识时，首先对粒子权重进行修正［16］，进一步采用全局最优位置变异PSO算法。算例分析表明，本文提出的改进PSO算法可提高风力发电机组的参数辨识精度。

1 DFIG模型及参数的可辨识性

双馈风力发电机组包括机械部分、双馈感应发电机以及控制器等模块［17］。

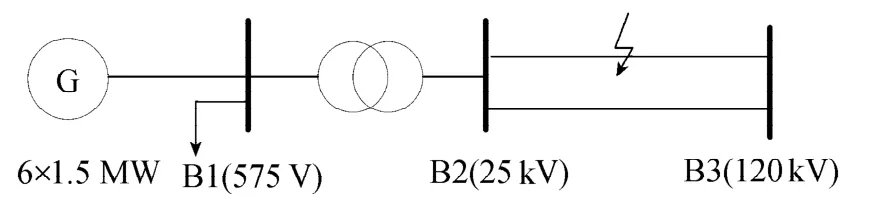
图1 MATLAB中DFIG接入到120 kV系统Fig.1 DFIG integrated with a 120kV power system in MATLAB

以MATLAB/Simulink平台中含双馈感应发电机(DFIG)的无穷大系统为例。如图1所示，风电场为6台容量为1.5 MW的双馈感应发电机，B1、B2和B3母线的基准电压分别为575 V、25 kV和120 kV。DFIG各参数分别为:定子电阻Rs=0.007 6 pu，定子电感Ls=0.171 pu，转子电阻Rr=0.005pu，转子电感Lr=0.156pu，定转子绕组互感Lm=2.9 pu。

扰动设置为t=0 s在B2～B3的单回线路中间发生瞬时性三相短路故障，0.15 s切除故障，系统恢复至原状态，仿真步长为0.001s，仿真时间为0.4s。以发电机有功功率作为观测变量，根据文献［18］定义的轨迹灵敏度指标，计算得到参数Rs、Ls、Lm、Rr、Lr的轨迹灵敏度，见图2。

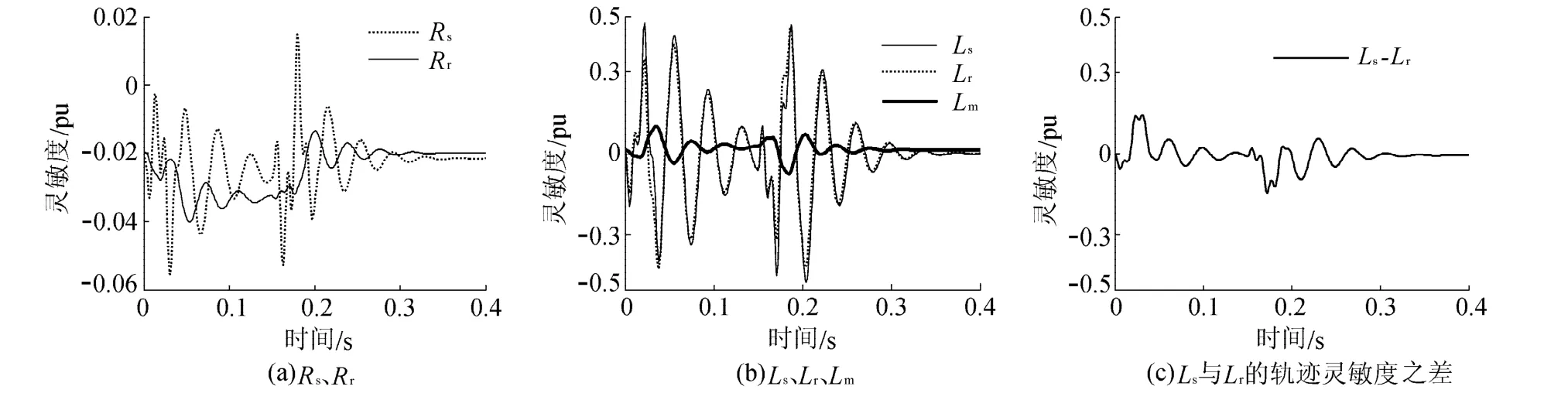
图2 参数的轨迹灵敏度曲线Fig.2 Trajectory sensitivities of DFIG parameters

从图2轨迹灵敏度的相位来看，只有参数Ls和Lr的灵敏度相位比较接近，但从图2(c)可以看出，两者的灵敏度相位不完全重合，因此所有参数均可区分辨识。从轨迹灵敏度大小来看，Ls和Lr的灵敏度高，容易辨识，Lm次之，Rs和Rr灵敏度较小，其中Rr的灵敏度最小，辨识难度大。

2 基本PSO算法

根据DFIG在电网侧故障下的有功功率受扰轨线，辨识DFIG各参数θ=［Rs，Ls，Lm，Rr，Lr］。参数辨识的目标是寻找待辨识参数^θ，使得仿真轨线 ^ysim与实测轨线yreal间的误差达到最小。目标函数为

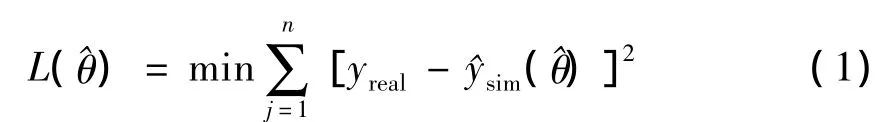
由式(1)可知参数辨识实际上是非线性优化问题，优化算法的选择将直接影响参数辨识的精度。由于基本PSO算法具有全局性能好、搜索效率高等优点，先采用基本PSO算法辨识风力发电机各参数。在基本PSO算法中，惯性权重w一般设置为常数。胡建秀等［19］指出:w较大，基本PSO方法的全局搜索能力强，局部搜索能力弱;w较小则相反。

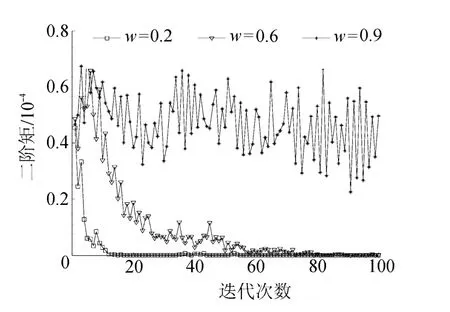
图3 参数辨识误差的二阶中心矩Fig.3 Second-order central moments of identified errors

设置与前文相同的故障，各参数的初值搜索范围设置为真值的［-30%，30%］。基本PSO算法中粒子大小为5，种群大小取30，迭代次数设置为100，学习因子设置为2。图3为不同惯性权重下基本PSO方法迭代次数与参数辨识误差。

50次参数辨识结果均值误差(相对值)见表1。

由图3可以看出，w较大时，种群较分散，PSO粒子在全局范围内粗略搜索，算法收敛慢;w较小时，种群聚集度较高，收敛快，PSO粒子侧重于某一局部区域的精细搜索。由表1可以看出，不同w下的参数辨识精度不同:过大或过小的w导致较大的参数辨识误差［20］。

3 改进PSO算法的DFIG参数辨识

由上述分析可以看出，固定的权重难以确定，且很难做到全局范围粗略搜索和局部区域的精细搜索同时最优。考虑到基本PSO算法易陷于早熟问题，本文提出将自适应变权重PSO算法和全局最优位置变异PSO算法相结合的改进PSO算法，用于DFIG参数辨识。

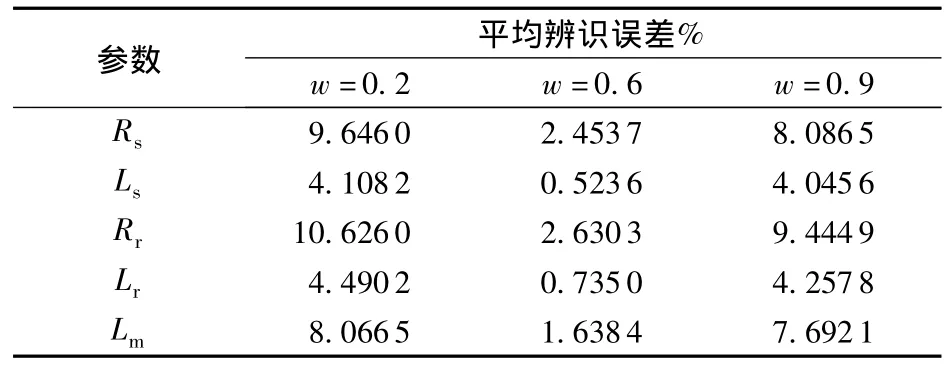
表1 不同惯性权重下的50次参数辨识结果均值的误差Table 1 Average values of identified errors for 50 iterations under different inertia weights

3.1 自适应变权重PSO算法

粒子w过大或过小都可能影响参数的辨识精度。为此，采用文献［16］提出的惯性权重线性递减(linearly decreasing weight，LDW)策略，使w随着迭代次数t的增加而线性递减，即

式中:wmin——惯性权重的最小值，设置为0.2;wmax——惯性权重的最大值，设置为0.9;Tmax——总迭代次数，设置为100。

自适应变权重PSO算法在种群进化前期采用较大的w，使得粒子运动速度大，全局搜索能力强;进化后期采用较小的w，使得粒子运动速度降低，着重于局部搜索，提高最优粒子的精度。

3.2 全局最优位置变异PSO算法

王海峰等［15］指出:当种群最优点连续多次都没有得到改进时，需对粒子群的全局最优位置进行1次变异，粒子群的全局最优位置尽可能地变化，使得整个粒子群不至于因全局最优位置处于某个局部最优点时的强大吸引而快速聚集到局部最优点。

对于种群中的每个粒子，其是否需要变异还需满足2个条件:(a)该粒子不是适应值最优的粒子;(b)生成1个0～1之间的随机数，且该随机数小于变异率。第i个粒子xi的变异公式如下:

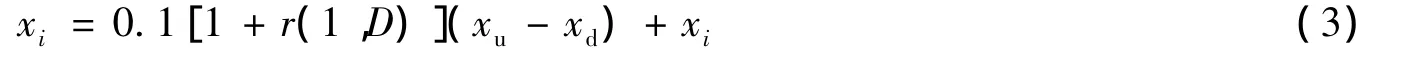
式中:xu、xd——搜索空间的上下限;r(1，D)——服从正态分布的D维随机向量。

3.3 基于改进PSO算法的参数辨识步骤

基于改进PSO算法的DFIG参数辨识步骤如下:(a)仿真/实测得到DFIG的有功功率受扰轨线;(b)设置粒子大小、初始位置、速度以及迭代次数;(c)根据当前的粒子参数仿真得到有功功率曲线受扰轨线，与真实有功功率轨线对比，计算粒子的适应度;(d)更新当前粒子历史最优适应度和相应的粒子位置、种群最优适应度和相应的粒子位置;(e)按照式(2)求解w，计算粒子的速度和粒子的位置;(f)求解粒子变异时机并对合适的粒子进行变异;(g)判断是否达到迭代次数或收敛阈值:若达到，输出种群最优粒子，结束;否则转向(c)。

将参数的搜索范围扩大到真值的［-80%，70%］，分别采用w=0.6的基本PSO算法、自适应变权重PSO算法、全局最优位置变异PSO算法以及改进PSO算法，基本PSO和改进PSO算法50次辨识的平均适应度随迭代次数的变化曲线见图4，50次DFIG参数辨识结果误差见表2。

由表2可知，与基本PSO算法、自适应变权重PSO算法和全局最优位置变异PSO算法相比，即使在较大的搜索范围内，改进PSO算法的参数辨识结果仍具有较高的辨识精度;由图4可知，改进PSO算法还具有较快的收敛速度。将改进PSO方法辨识得到的参数代入系统模型中，计算有功功率受扰曲线，并与实际轨线相比较，结果见图5。可以看出，辨识轨线的拟合精度较高。

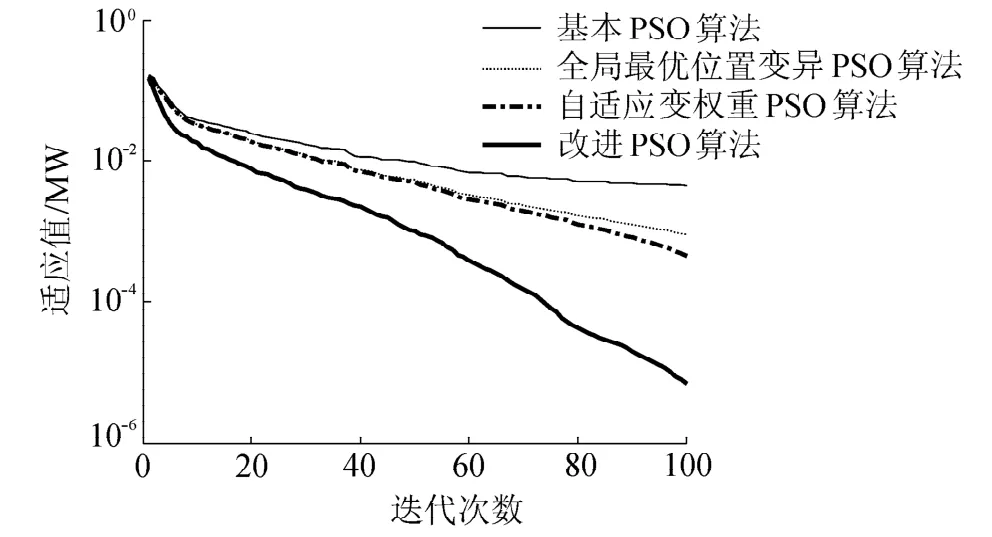
图4 基本PSO和改进PSO的适应度进化曲线Fig.4 Fitness curves with basic PSO algorithm and improved PSO algorithm

图5 实际受扰轨线与基于辨识值的受扰轨线Fig.5 Real disturbed trajectory and identified disturbed trajectory

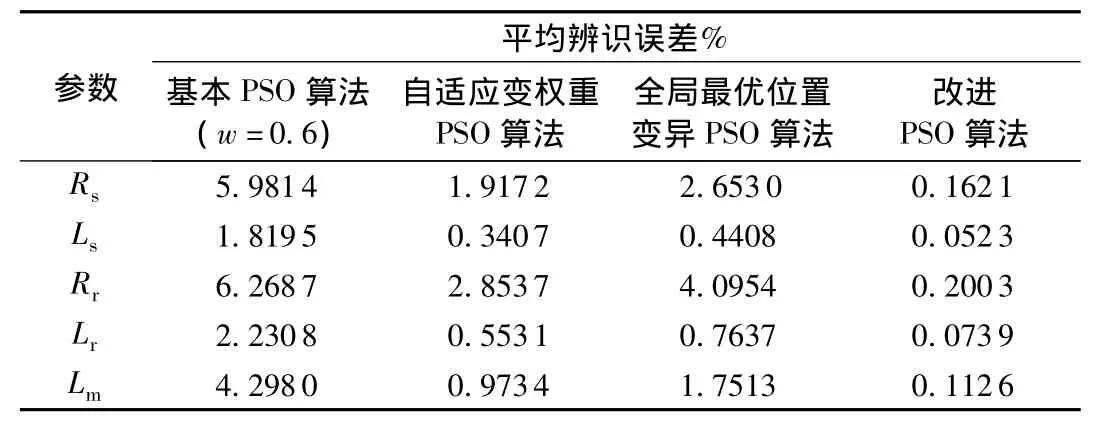
表2 不同PSO算法的参数辨识误差Table 2 Errors identified with different PSO algorithms

4 结 论

基本PSO算法采用固定的权重，辨识结果表明，采用较小的权值基本PSO算法容易陷入局部最优，过早收敛;采用较大的权值，基本PSO算法容易找到全局最优附近，但是辨识参数值的精度不高;同时由于基本PSO算法存在早熟问题，为此本文提出将自适应变权重PSO算法和全局最优位置变异PSO算法相结合的改进PSO算法，用于双馈感应发电机参数辨识。辨识结果表明，改进PSO算法不仅收敛速度较快，且辨识精度较高。即使在较大的初始搜索范围内仍具有较高的辨识精度，因此该方法的鲁棒性和适应性好。

从参数辨识结果可以看出，参数Ls和Lr的灵敏度大，辨识精度高;参数Lm的灵敏度较大，辨识精度较高;参数Rr的灵敏度最小，辨识误差较大。

［1］孙元章，吴俊，李国杰.风力发电对电力系统的影响［J］.电网技术，2007，31(20):55-62.(SUN Yuanzhang，WU Jun，LI Guojie.Influence research of wind power generation on power systems［J］.Power System Technology，2007，31(20):55-62.(in Chinese))

［2］ASMINE M，BROCHU J，FORTMANN J，et al.Model validation for wind turbine generator modelsK［J］.IEEE Transactions on Power Systems，2011，26(3):1769-1782.

［3］张仰飞，袁越，陈小虎，等.风力机参数的可辨识分析［J］.电力系统自动化，2009，33(6):86-88.(ZHANG Yangfei，YUAN Yue，CHEN Xiaohu，et al.Analysis on wind turbine parameters identifiability［J］.Automation of Electric Power Systems，2009，33(6):86-88.(in Chinese))

［4］张仰飞，李海峰，王伟胜，等.变桨距风电机组最佳叶尖速比的拟合求取［J］.河海大学学报:自然科学版，2012，40 (2):229-232.(ZHANG Yangfei，LI Haifeng，WANG Weisheng，et al.Optimal blade tip speed ratio fitting of variable-pitch wind turbines［J］.Journal of Hohai University:Natural Sciences，2012，40(2):229-232.(in Chinese))

［5］张建华，辛付龙，陈星莺，等.双馈风力发电机三相短路状态下的参数辨识［J］.电力自动化设备，2012，32(6):86-89. (ZHANF Jianhua，XIN Fulong，CHEN Xingying，et al.Parameter identification of DFIG with three-phase short circuit［J］. Electric Power Automation Equipment，2012，32(6):86-89.(in Chinese))

［6］金宇清，赵泽，鞠平，等.双馈感应风力发电机的参数辨识分析［J］.高电压技术，2011，37(7):1700-1705.(JIN Yuqing，ZHAO Ze，JU Ping，et al.Analysis on the identification of doubly fed induction generator［J］.High Voltage Engineering，2011，37(7):1700-1705.(in Chinese))

［7］张仰飞，袁越，陈小虎，等.优选初值-微变搜索算法及其在双馈风力发电机参数辨识中的应用［J］.电力自动化设备，2010，30(2):19-21.(ZHANG Yangfei，YUAN Yue，CHEN Xiaohu，et al.Preferred initial value-slightly changed search algorithm in the double-fed wind generator parameter identification［J］.Electric Power Automation Equipment，2010，30(2): 19-21.(in Chinese))

［8］MARINO P，MUNGIGUERRA V，RUSSO F，et al.Parameter and state estimation for induction motors via interlaced least squares algorithm and Kalman filter［C］//27th Annual IEEE Power Electronics Specialists Conference.New York:IEEE Computer Society Press，1996:1235-1241.

［9］SAG T，CUNKAS M.Multi-objective genetic estimation to induction motor parameters［C］//International Aegean Conference on Electrical Machines and Power Electronics and Electron-motion ACEMP’07 and Electromotion’07 Joint Conference.New York: IEEE Computer Society Press，2007:628-631.

［10］URSEM R K，VADSTRUP P.Parameter identification of induction motors using differential evolution［C］//IEEE Congress on Evolutionary Computation.New York:IEEE Computer Society Press，2003:790-796.

［11］EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory［C］//Proceedings of the sixth international symposium on micro machine and human science.Nagoya:IEEE Computer Society Press，1995:39-43.

［12］程颖，鞠平，吴峰.负荷模型参数辨识的粒子群优化法及其与基因算法比较［J］.电力系统自动化，2003，27(11):25-29.(CHEN Ying，JU Ping，WU Feng.PS algorithm in load parameter identification and its comparison with genetic algorithm［J］.Automation of Power Systems，2003，27(11):25-29.(in Chinese))

［13］GONZALEZ-LONGATT F，REGULSKI P，WALL P，et al.Fixed speed wind generator model parameter estimation using improved particle swarm optimization and system frequency disturbances［C］//Conference on Renewable Power Generation. Edinburgh United Kingdom:IET，2011:1-5.

［14］胡家声，郭创新，曹一家.基于扩展粒子群优化算法的同步发电机参数辨识［J］.电力系统自动化，2004，28(6):35-40.(HU Jiasheng，GUO Chuangxin，CAO Yijia.Generator parameter identification based on extended particle swarm optimization method［J］.Automation of Power Systems，2004，28(6):35-40.(in Chinese))

［15］王海峰，刘晶晶.全局最优位置变异粒子群优化算法［J］.青岛理工大学学报，2009，30(5):93-97.(WANG Haifeng，LIU Jingjing.The particle swarm optimization algorithm of global optimum location mutation［J］.Journal of Qingdao Technological University，2009，30(5):93-97.(in Chinese))

［16］SHI Y，EBERHART R C.Empirical study of particle swarm optimization［C］//Proceedings of the 1999 Congress on Evolutionary Computation.Washington D C:IEEE Computer Society Press，1999:1945-1950.

［17］WU F，ZHANG X P，GODFREY K，et al.Small signal stability analysis and optimal control of a wind turbine with doubly fed induction generator［J］.IET Generation，Transmission＆Distribution，2007，1(5):751-760.

［18］鞠平.电力系统建模理论与方法［M］.北京:科学出版社，2010:215-300.

［19］胡建秀，曾建潮.微粒群算法中惯性权重的调整策略［J］.计算机工程，2007，33(11):193-195.(HU Jianxiu，ZENG Jianchao.Selection on inertia weight of particle swarm optimization［J］.Computer Engineering，2007，33(11):193-195.(in Chinese))

［20］TRELEA I.The particle swarm optimization algorithm:convergence analysis and parameter selection［J］.Information Processing Letters，2003，85(6):317-325.