棱形液舱内液体晃荡问题的SPH数值模拟

刘谋斌，周 冉，邵家儒

(中国科学院力学研究所流固耦合系统力学重点实验室，北京 100190)

在未充满液体的容器内，液体在外界激励下的运动称为液体晃荡(或晃动，sloshing)。实际工程中存在很多晃荡现象，如载液货船(航行中的大型原油货轮(VLCC)、液化石油气船(LPG)、液化天然气船(LNG))、飞行中的火箭液体燃料舱、地震时核反应炉和水库等都涉及晃荡问题［1］。晃荡流体由具有轻重差异、互不相溶的2种流体组成(一般是气液两相流)，因此液体晃荡的一个显著特点是存在自由液面或运动界面［2］。当外界激振力振动幅度较大，或者激振力频率与晃荡系统固有频率接近甚至一致时，容器内的液体可能产生剧烈的振荡并对承载容器产生巨大的冲击压力。液体晃荡作为一类相当复杂的运动现象，已成为工程流体力学领域的一个基础性与前沿性研究课题，具有极其重要的科学意义和工程应用价值。

晃荡研究最初是在航空航天与核工业领域里进行，经过几十年的发展，已经形成了三大类研究方法——理论研究、实验研究和数值计算。近年来随着计算机技术的飞速发展，数值模拟方法在晃荡问题中得到了广泛应用，如有限元法、有限差分法、边界元法及粒子法［3-4］等。Nakayama和Washizu［5］用有限元法计算了势流的晃荡问题。朱仁庆等［6］采用VOF(volume of fluid)法模拟了盛液容器内液体的二维晃荡。Faltisen［7］用边界元法计算了矩形容器的液体晃荡，考虑了非线性自由表面条件并引入人工黏性克服瞬态项的影响。

光滑粒子动力学SPH方法(以下简称SPH方法)最早是由Gingold等［8］以及Lucy［9］各自独立地提出，最初用于模拟分析天体物理问题，是一种拉格朗日无网格粒子法［10］。它利用核函数对物理问题进行近似处理，把连续的物质空间离散到一系列无序分布的可运动粒子上，用离散的粒子代替连续分布的流体，在模拟具有自由表面的液体晃荡问题中，粒子是运动的，可以有效捕捉液面的位置和运动，处理大变形问题［11］。Iglesias等［12］用SPH方法对液舱晃荡所产生的力矩幅值进行了计算。崔岩等［13］运用SPH方法对二维矩形水槽的纵荡过程和纵摇过程进行数值模拟，分析激励频率接近容器一阶固有频率时的晃荡现象，讨论纵荡和纵摇综合作用对流体运动的影响。Shao等［14］应用改进的SPH方法研究了二维矩形水箱内的液体晃荡，结果显示改进的SPH方法能够获取光滑、准确的压力场，能有效模拟大幅度液体晃荡。

笔者应用SPH方法对棱形液舱内的液体晃荡问题进行数值模拟，将计算结果与实验结果进行对比，并进一步研究不同充液比、激励频率对晃荡行为的影响。

1 SPH方法基本理论

在SPH方法中，计算域用一系列的粒子来描述，粒子是整个场变量近似的计算框架，每个粒子包含独自的材料性质如质量、密度等，在内外力的作用下按照守恒控制方程的规律运动。传统SPH方法对偏微分方程的近似由核近似和粒子近似2部分组成。核近似是对函数及其导数函数进行连续形式的近似，通过对函数本身与某个核函数之积的积分得到。粒子近似则是对粒子支持域内的所有粒子加权求和。

SPH形式的控制方程为

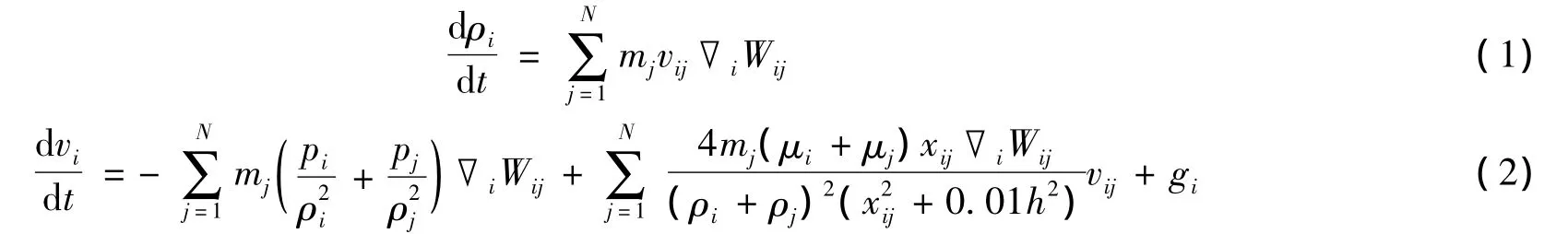
式中:ρ——流体密度;t——时间;N——支持域内的粒子数;m——粒子质量;v——粒子的速度;W——光滑函数;p——压强;μ——动力黏性系数;h——光滑长度;x——粒子的位置;g——重力加速度;rij——粒子i和粒子j之间的距离。

传统的SPH方法精度较低，尤其是在粒子分布不均匀的区域(如边界处粒子支持域被截断)，不能准确重构二次和线性函数，甚至无法精确重构一个常数，导致传统SPH方法求解精度和稳定性降低。笔者采用密度修正和核梯度修正改进传统SPH方法［14］。通过恢复核函数在粒子分布不均匀区域的归一化性质对密度进行修正，使密度趋近初始密度，满足不可压流体的特性。核梯度修正在二维情况下可以表示为

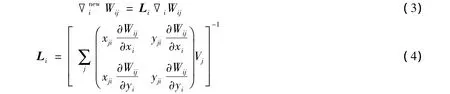
式中:Vj——粒子j的体积。

基于核梯度修正的SPH算法具有二阶精度，并且可以在不改变传统SPH程序整体框架的条件下方便实施。

在SPH数值模拟中，对于固壁边界很难像网格方法那样严格实施。边界上或邻近边界处粒子的支持域往往被边界截断，这些粒子通常只受到边界内粒子的影响，这种单边影响作用会使误差持续积累，影响最终的模拟结果。笔者应用改进的耦合动力学边界法［15］，用两类粒子完成整个固壁边界的构建。第1层虚粒子布置在边界处，对于靠近边界的流体粒子将产生排斥力。另2层虚粒子布置在固壁边界外部，初始时刻即生成，且不需与内部流体粒子关于边界镜像对称，位置不需要随时间推进而改变。

2 棱形液舱液体晃荡

图1 棱形液舱模型示意图(单位:mm)Fig.1 Model of prismatic tank(units:mm)

随着海洋运输的发展和能源需求的提高，棱形液舱被广泛应用于大型载液货船储液系统设计中。Mikelis等［16］在实验中通过对棱形液舱施加横摇及俯仰激励，测量液体晃荡对液舱侧壁及顶部产生的冲击压力。液舱的晃荡实验满足模型相似律，即几何相似、运动相似、动力相似、边界条件相似及初始条件相似。实验模型按1∶40的比例制作，在液舱的侧壁上布置压力测试点。笔者采用二维模型，模拟和分析了有无内部隔板时棱形液舱内的液体晃荡行为。图1给出了液舱尺寸及文中计算工况所用到的压力测试点布置。测点A、B、C分别距离液舱底部75 mm、113.5 mm、205 mm，压力分别表示为P1、P2、P3。外加激励为绕转轴的横摇运动，转轴距离舱底194 mm，激励运动方程为［17］

式中:θ0——最大转角，取0.1 rad;ω——角速度。

2.1 不带隔板棱形液舱液体晃荡

笔者在2种工况下对不带隔板的棱形液舱进行数值模拟，追踪压力P1、P2、P3的时间历程，并将模拟结果与实验结果进行对比。

工况1中，外界激励周期T=1.517s，充液比h/H=0.33(H为液舱的高度)，水体粒子数为9330，总粒子数为11439。图2给出t=3.0～4.5s约一个周期的液面形状变化。在不同的激励周期和充液比等参数影响下，液体晃荡可以表现为多种复杂的形式。常见的液体晃荡现象有驻波、行进波、水跃以及组合波，还有可能在冲击作用下表现出液体的翻卷和飞溅等强非线性现象。图2直观地显示了液舱在横摇激励作用下较明显的行进波及轻微的飞溅现象。图3为压力P1、P2、P3的历程与实验结果对比，压力的最大峰值及周期变化基本吻合，在时间上略有滞后可能是由于实验数据选取时刻上的误差所致。由图3可知，压力呈现双峰特性，这是晃荡过程中液体迟滞特性的典型表现。前一个峰值是由液体对舱壁冲击产生的高脉冲压力，具有瞬时性，主要发生在水跃或行进波中;后一个峰值也是由冲击产生的脉冲压力，但是时间相对较长，峰值较小，主要是由于液体快速连续地作用在未被完全淹没的舱壁，压力具有连续性［17］。

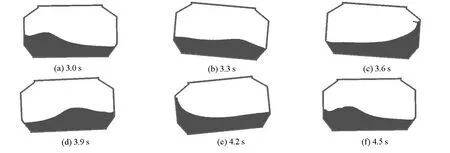
图2 工况1典型时刻的自由液面形状变化Fig.2 Evolutions of free surface at typical time instants obtained from case 1

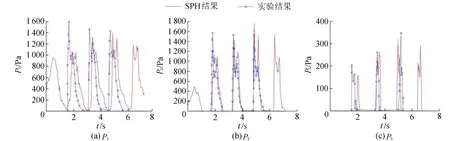
图3 压力P1、P2、P3的时间历程Fig.3 Pressure time histories of three observation points，P1，P2，and P3

工况2中，外界激励周期T=1.112s，充液比h/H=0.61，水体粒子数为19416，总粒子数为21525。图4给出了t=3.0～4.1 s约一个周期的液面形状变化。可以看到在大充液比下，由冲击产生较剧烈的液体飞溅，并且模拟出液面的翻卷和碎波现象。图5为P2的历程与实验结果的对比，压力的最大峰值及周期变化趋势基本吻合，在时间上略有滞后可能是由于实验数据读取时刻上的差异所致。通过与工况1中P2的对比，可以看到在大充液比情况下晃荡剧烈，液体对舱壁产生较大的冲击，压力值明显比工况1增大许多。

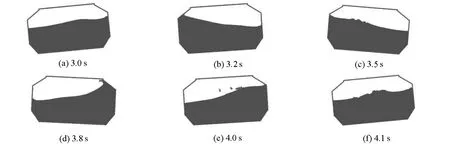
图4 典型时刻工况2的自由液面形状变化Fig.4 Evolutions of free surface at typical time instants obtained from case 2

2.2 带隔板棱形液舱液体晃荡

为进一步研究液舱结构对液体晃荡特性的影响，笔者对带隔板的棱形液舱液体晃荡问题进行了数值模拟。隔板布置在液舱的中部，隔板高度为95 mm，见图1。其他参数与不带隔板的工况1情况相同。

图6为t=3.8～4.5 s约一个周期的速度矢量图。通过与不带隔板的情况(图2)进行对比，可知加设隔板后液体晃荡幅度大幅度减弱，晃荡较平稳，没有出现强烈的冲击壁面以及飞溅等现象。图7为P2历程与不加隔板情况的对比，明显看到加设隔板后的压力值大幅度减小，并且双峰特性基本消失，只有一个比较光滑平稳的压力峰值。由此表明，隔板的阻挠减缓了液体向另一侧的流动，大幅度消除了液体对舱壁的冲击作用，能够有效地抑制液舱的晃荡。在生产实际中，人们往往选用在舱内加隔板，达到抑制晃荡的目的。加设隔板不仅有防晃作用，而且不影响舱容，因此在生产实际中得到广泛应用。不过一些具体问题还应当具体分析，不能一概而论［18］。

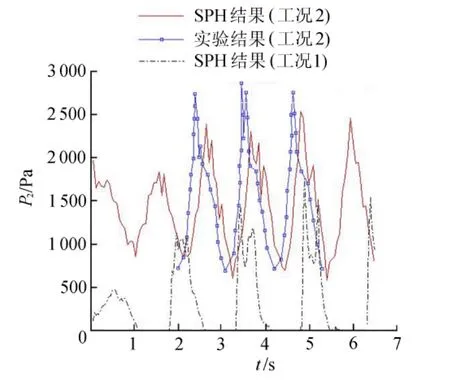
图5 P2压力历程Fig.5 Pressure time history at point P2

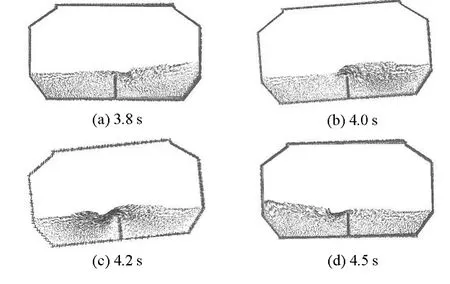
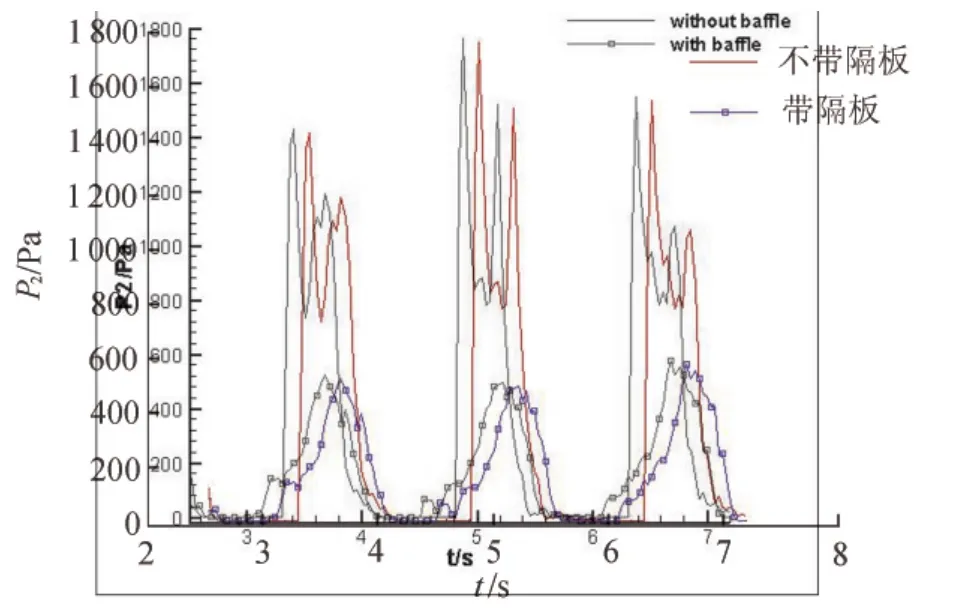
图7 P2压力历程对比Fig.7 Comparison of pressure time histories at point P2under different conditions

3 结 语

应用改进的SPH方法对棱形液舱中的液体晃荡现象进行了数值模拟与研究。首先对棱形液舱在外加正弦激励作用下的自由液面晃荡进行了数值模拟，研究不同激励周期及充液比的液体晃荡问题，模拟结果与实验结果吻合较好，且能够捕捉到压力的双峰特性及波浪翻卷、飞溅等复杂现象。另外，通过改变舱体结构，对带有隔板的棱形液舱进行了研究，结果表明通过合理改变舱体结构可以有效地抑制晃荡现象。

［1］娜日萨.VLCC液舱晃荡仿真及结构强度评估方法研究［D］.哈尔滨:哈尔滨工程大学，2006.

［2］李晓明.船舶液舱晃荡载荷及结构强度的工程计算方法［D］.武汉:华中科技大学，2007.

［3］朱仁庆，吴有生，彭兴宁，等.船舶液体晃荡动力学的研究方法及进展［J］.华东船舶工业学院学报，1999，13(1):45-47. (ZHU Renqing，WU Yousheng PENG Xingning，et al.Study and advance of liquid sloshing dynamics of ship［J］.Journal of East China Shipbuilding Institute，1999，13(1):45-47.(in Chinese))

［4］陆志妹，范佘明.船舶液舱晃荡研究进展［J］.上海造船，2010(2):14-17.(LU Zhimei，FAN Sheming.Study advance of liquid sloshing of ship［J］.Shanghai Shipbuilding，2010(2):14-17.(in Chinese))

［5］NAKAYAMA T，WASHIZU K.Nonlinear analysis of liquid motion in a container subjected to forced pitching oscillation［J］. International Journal for Numerical Methods in Engineering，1980，15(8):1207-1220.

［6］朱仁庆，颜开，吴有生.盛液容器内液体二维晃荡的数值模拟［J］.华东船舶工业学院学报，1998，12(2):14-21.(ZHU Renqing，YAN Kai，WU Yousheng.Two dimensions numerical simulation of liquid sloshing in tanks［J］.Journal of East China Shipbuilding Institute，1998，12(2):14-21.(in Chinese))

［7］FALTINSEN O M.A numerical nonlinear method of sloshing in tank with two dimensional flow［J］.Journal of Ship Research，1978，22(3):193-202.

［8］GINGOLD R A，MONAGHAN J J.Smoothed particle hydrodynamics-theory and application to non-spherical stars［J］.Monthly Notices Royal Astronomical Society，1977，181:375-389.

［9］LUCY L B.A numerical approach to the testing of the fission hypothesis［J］.Astronomy Journal，1977，82:1013-1024.

［10］LIU Guirong，LIU Moubin.Smoothed particle hydrodynamics:a meshfree particle method［M］.Singapore:World Scientific，2003.

［11］谬吉伦，陈景秋，张永祥.SPH方法在自由表面流体研究中的应用［J］.水利水电科技进展，2011，31(3):20-23.(MIU Jilun，CHEN Jingqiu，ZHANG Yongxiang.Application of SPH method to studies on free surface flows［J］.Advances in Science and Technology of Water Resources，2011，31(3):20-23.(in Chinese))

［12］IGLESIAS A S，DELORME L，ROJAS L P，et al.Liquid moment amplitude assessment in sloshing type problems with smooth particle hydrodynamics［J］.Ocean Engineering，2006，33(11/12):1462-1484.

［13］崔岩，吴为，龚凯，等.二维矩形水槽晃荡过程的SPH方法模拟［J］.水动力学研究与进展，2008，23(6):618-624.(CUI Yan，WU Wei，GONG Kai，et al.Numerical simulation of sloshing in two dimensional rectangular tanks with SPH［J］.Chinese Journal of Hydrodynamics，2008，23(6):618-624.(in Chinese))

［14］SHAO Jiaru，LI Huiqi，LIU Guirong，et al.An improved SPH method for modeling liquid sloshing dynamics［J］.Computer and Structures，2012，100-101:18-26.

［15］LIU Moubin，SHAO Jiaru，CHANG Jianzhong.On the treatment of solid boundary in smoothed particle hydrodynamics［J］. Science China Technological Sciences，2012，55(1):244-254.

［16］MIKELIS N E，MILLER J K，TAYLOR K V.Sloshing in partially filled liquid tanks and its effect on ship motions:numerical simulations and experimental verification［J］.The Royal Institution of Naval Architects，1984，126:267-277.

［17］刘富，童明波，陈建平.基于SPH方法的三维液体晃动数值模拟［J］.南京航空航天大学学报，2010，42(1):122-126. (LIU Fu，TONG Mingbo，CHEN Jianping.Numerical simulation of three-dimensional liquid sloshing based on SPH method［J］. Journal of Nanjing University of Aeronautics＆Astronautics，2010，42(1):122-126.(in Chinese)

［18］端木玉，朱仁庆，陈正云，等.不同液舱结构形式对晃荡的影响分析［J］.水动力学研究与进展，2006，21(6):760-769. (DUAN Muyu，ZHU Renqing，CHEN Zhengyun，et al.Analysis on sloshing of different ship tanks［J］.Chinese Journal of Hydrodynamics，2006，21(6):760-769.(in Chinese))