基于Madaline网络敏感性的主动学习算法研究

曾晓勤，赵倩倩，何嘉晟

(河海大学计算机与信息学院，江苏南京 210098)

近年来，主动学习成为机器学习领域的研究热点。传统的监督学习算法多是被动学习，即只能被动接受指定的数据，要求训练样本中含有标注数据。然而，在很多实际问题中，如文本分类、图像检索、语音识别等往往含有大量的未标注数据，只有少量的标注数据，这使得监督学习算法在应用上存在很大的局限性［1］。另外，对样本进行数据标注常常比较困难，甚至代价十分昂贵，而获取未标注数据的样本则相对容易。如针对基因序列的测试，标注一段基因序列需要进行代价昂贵的实验，相反，获取基因片段代价则相对小的多［2］。在有大量标注数据的情况下，选择尽可能少的、有代表性的样本进行学习，将大幅度提高学习效率。

主动学习一般分为两部分:学习器和选择器。学习器可以是一个分类器，用于学习标注数据的样本，算法也多是监督学习中常见的算法。选择器用于选择未参加学习的、标注或未标注数据样本，是主动学习的核心。主动学习与传统被动学习最本质的区别是多了一个主动选择的过程，可以自主地选择最有“价值”的样本(对于未标注数据的，需交由专家进行标注)，然后再带回学习。显然，对适用于少量标注数据与大量未标注数据共存情况的主动学习进行研究既具有学术研究的意义，也具有实际应用的价值。根据获得未标注数据样本方式的不同，可以将主动学习算法分为2种类型:基于流的主动学习［3-5］和基于池的主动学习［6-8］。

Madaline网络是一种通用的前馈离散型多层网络。理论上，离散问题可作为连续问题的特例，所以可以用连续前向网络代替离散前向网络。但是，对于那些本质为离散，且连续技术难以适用的领域，如逻辑运算、分类以及聚类等，离散前向网络直接突显出简单和高效的优势。激活函数的不连续性使得离散前向网络不能再使用成熟的BP算法［9-10］。Winter等［11-12］对Madaline网络训练算法进行了研究，提出了著名的MRII算法。MRII算法把对网络的训练转化为对每个Adaline的训练，以最小扰动原则为依据，通过不断的翻转与迭代找到最佳的权值。近些年，Zhong等［13］在MRII算法的基础上，利用Madaline网络的敏感性技术，对Madaline网络训练算法进行了进一步的研究和改进。

一般而言，神经网络敏感性是研究因网络参数的扰动而引起网络输出发生变化的情况［14］，需找出网络输出变化与网络参数扰动之间的依赖关系。若考虑参数仅为输入情况，由于不同输入样本的扰动可能引起输出的不同变化，所以针对样本扰动的网络敏感性可以用来衡量网络输出对于不同输入样本的敏感程度。以网络敏感性为尺度，不难给出如下2种解释和推论:(a)那些使得网络输出敏感性大的样本(称为敏感样本)离网络已建立起的判定边界一定相对较近，因而类似支持向量在支持向量机中扮演的角色，敏感样本值得挑选出来进行进一步精化训练;(b)那些使得网络输出敏感性小的样本(称为不敏感样本)离网络已建立的判定边界一定相对较远，如果不敏感样本与已参加训练的所有样本距离都较远，说明网络前期训练中缺失了这种样本所代表的信息，因而也需挑选出来进行进一步全面训练。所以，在处理分类问题的主动学习中，Madaline网络敏感性可以作为一个合适的尺度，用来主动挑选尚未训练的样本参加训练，显然，策略是挑选那些对当前Madaline网络敏感性大或小的样本。

由以上所述可见，主动学习过程中，关键是如何从大量的未标注数据样本中挑选最有“价值”的样本进行学习。本文提出一种新的主动学习算法，即基于Madaline网络敏感性的主动学习算法。

1 Madaline网络模型及符号约定

神经元Adaline是神经网络Madaline的基本构成单元，组成网络中的一个节点。

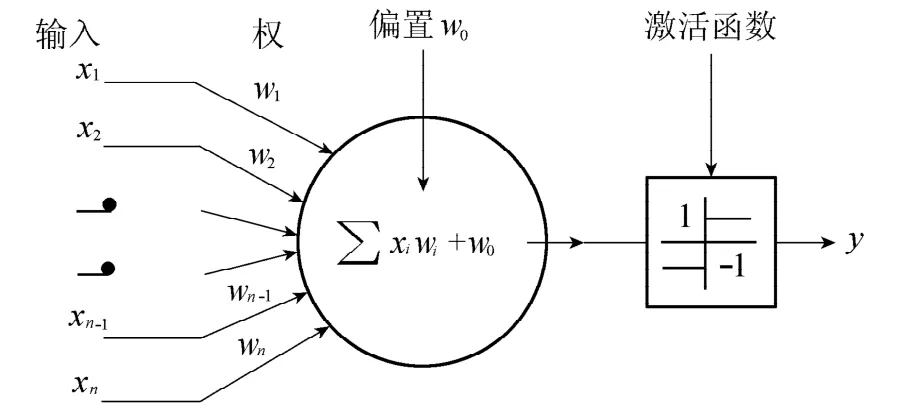
图1 Adaline结构示意图Fig.1 Sketch map of Adaline structure

1.1 Adaline模型及符号

图1为一个神经元Adaline的结构示意图。

输入向量为

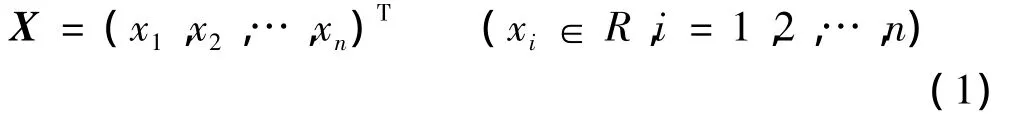
权向量为

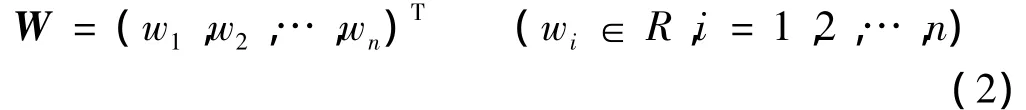
偏置为w0，激活函数为对称硬极限函数，即

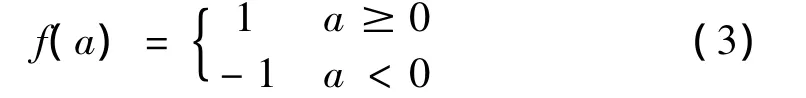
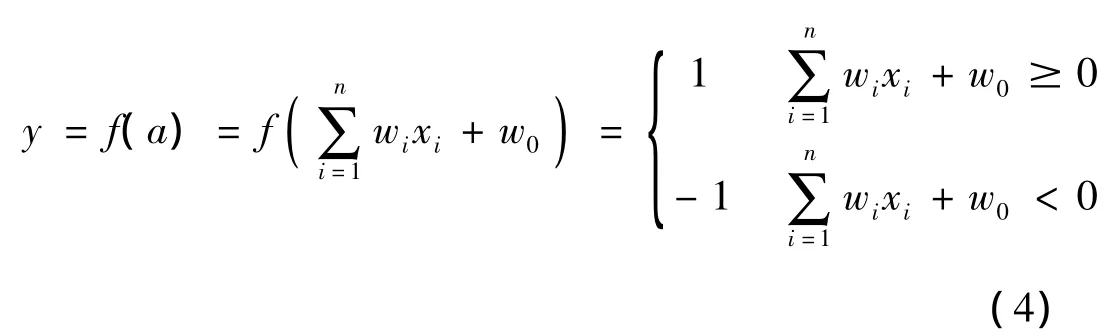
就功能而言，神经元Adaline实现了一种从多维空间向一维空间的逻辑映射关系。

1.2 Madaline网络模型及符号

Adaline是Madaline网络的最简单形式，Madaline网络可由Adaline根据一定的规则连接而成。图2是Madaline网络模型结构示意图，Xi、Yi(1≤i≤L)分别表示网络第i层的输入和输出。由本文介绍可知，Yk-1=Xk(2≤k≤L)。Madaline网络第一层输入X1是整个网络的输入，由样本的输入提供;最后一层输出YL作为整个网络的输出。为方便表达，用n0-n1-…-nL表示一个有L层的网络，n0为网络的输入维数，ni(1≤i≤L)为第i层上所包含的神经元个数。

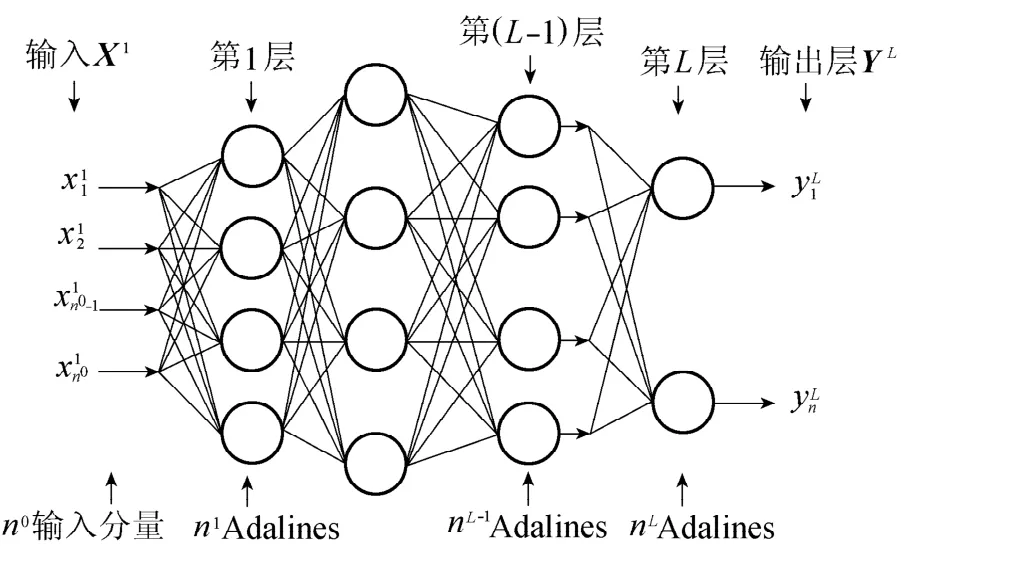
图2 Madaline网络模型Fig.2 Madaline network model

从功能上看，Madaline网络是在训练中通过一定的调整规则调整自身的参数(包括权值、偏置值或网络结构)来实现给定训练数据中输入与输出间的对应关系，建立从n0维空间到nL维空间某种特定的映射关系。

2 网络敏感性定义及计算

2.1 Adaline敏感性定义

影响Adaline输出变化的参数主要是权和输入。权决定输入与输出之间的映射关系，因而它的扰动必然会对输入和输出关系产生影响，进而使输出受到影响。权固定之后，输入决定了输出，输入扰动也势必会对输出产生影响。本文只考虑给定输入点的扰动对于输出的影响，因此，Adaline敏感性定义为:因某一给定输入点的可能变化而导致输出的变化，表示为

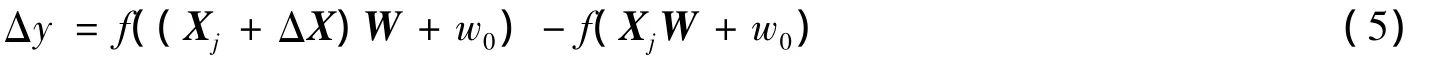
其中，输入点Xj和权值W都是固定的。显然，这个定义最自然和直接地表示了因输入点扰动ΔX而导致的输出变化Δy。

2.2 Madaline网络敏感性定义

设Madaline网络输入为Xn×1∈Rn，输出为Ym×1∈{-1，1}m，训练后的网络在输入和输出间建立的映射为G(X)=Y，又可表示为G(X)=(g1(X)，g2(X)，…，gm(X))T。对Madaline网络敏感性进行研究，已有文献［15-16］针对不同的网络参数扰动情况进行了讨论。本文在Adaline敏感性定义的基础上，定义Madaline网络敏感性为:因网络在某一给定输入点的可能变化而导致网络输出变化的概率P，表示为

其中，ΔX∈［-a，a］n(a＞0)视为一统计量，是邻近输入点Xj周围的可能变化量。式(6)将Madaline网络敏感性定义为在给定的输入点Xj处，由于ΔX而导致网络输出变化的概率。

2.3 Madaline网络敏感性计算

由式(6)可得

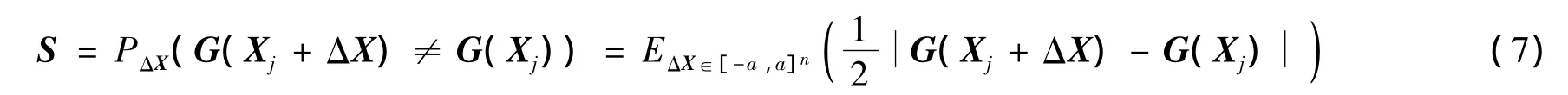
式中:E——期望值。则第i个分量的计算公式为

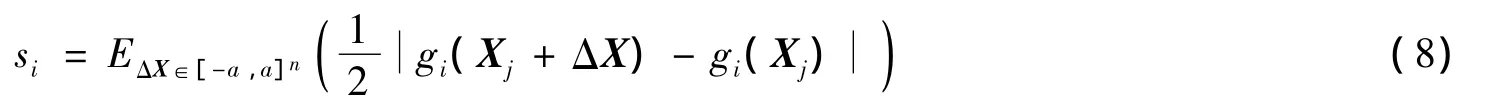
对Madaline网络敏感性计算，笔者给出一个简洁的近似计算方法，基本思路是，对输入扰动的每一个分量，在连续区间［-a，a］n内离散取点，然后计算输入扰动在所有可能离散点处的均值作为式(8)的近似值。显然，离散点取的越多越精确，但是计算复杂度将会呈指数级上升。

设第i个分量以步长h在区间［-a，a］均匀取k=2a/h+1个值，则式(8)可近似计算为:对于输入样本为Xj，输入变化范围为［-a，a］的网络G()=(g1()，g2()，…，gm())T，其第i个输出分量敏感性的计算，则为第i个输出分量的敏感性，其网络输出敏感性S(Xj，G，a)即S=(s1，s2，…，sm)T为网络在Xj的敏感性。

3 基于Madaline网络敏感性的主动学习算法

主动学习的基本思想是:(a)根据初始的标注数据样本集生成基础分类器，也就是利用监督学习算法对初始样本进行训练，得到一个粗分类器;(b)设计一个样本选择算法，该算法根据一定标准对提供的未参与训练的样本(已标注或未标注数据样本)进行评价，从中挑选一个或几个样本(未标注数据样本需交由专家进行标注)加入到训练数据集中，继续对基础分类器进行训练。学习器和选择器重复交替工作，逐步使分类器性能提高，直到达到预定目标停止。

基于Madaline网络敏感性的主动学习算法以Madaline网络为学习器，首先根据部分标注数据样本进行学习，得到一个基础Madaline网络，然后以该Madaline网络在那些给定但未参与训练样本点的敏感性为评价尺度，挑选敏感性大的样本(对未标注数据样本需先进行标注)加入初始训练样本集中继续训练，循环往复该过程，直到最终满足学习器的性能目标。算法中之所以没有挑选敏感性小的样本，是因为在确定初始训练样本集时，可先把所有给定的训练样本进行聚类，挑选每个类中的样本作为初始训练样本集，这样就可避免感性值小的样本与参加训练样本的距离较远的情况。基于Madaline网络敏感性的主动学习算法具体步骤如下。

a.将训练样本集X(其中有少量标注数据样本和大量未标注数据样本)聚类。

b.挑选每个类中的样本构成初始训练样本集^X(未标注样本需进行标注)。

c.循环执行以下操作直到满足终止条件:(a)用^X训练分类器G;(b)对所有未参与初始训练的样本Xj∈(X-^X)，计算其敏感性值S(Xj，G，a);(c)按敏感性值递减的方法对样本排序;(d)选取前k个样本加入到^X中(k值可视具体应用而定)。

d.返回G。

4 实验结果及分析

实验以VC++6.0为实验平台进行，使用UCI数据库中的Pima数据集(两分类)和Iris数据集(三分类)。对于两分类，在构建分类器时输出层含有1个Adaline神经元;对于三分类，在构建分类器时输出层含有2个Adaline神经元。把每组数据集分成两部分:75%的训练样本集和25%的测试样本集。在X中，首先将X进行聚类，然后挑选每个类中的样本构成 ^X，这些^X直接用于训练出一个粗分类器。根据主动学习的特性，在训练的过程中按照不同的挑选策略挑选参加训练的样本:(a)随机挑选策略，随机挑选未参与初始训练的样本加入到^X中继续对基础分类器进行训练;(b)基于Madaline网络敏感性的主动学习挑选策略，用该策略挑选未参与初始训练的样本加入到 ^X中继续对基础分类器进行训练。针对Pima数据集和Iris数据集，分别利用2种挑选策略进行了5组实验，每组实验针对相同的实验环境又做了10次，表1为每组实验的平均结果。

可以看出多数情况下本文提出的基于Madaline网络敏感性的主动学习算法比随机挑选的方法具有更高的准确率。

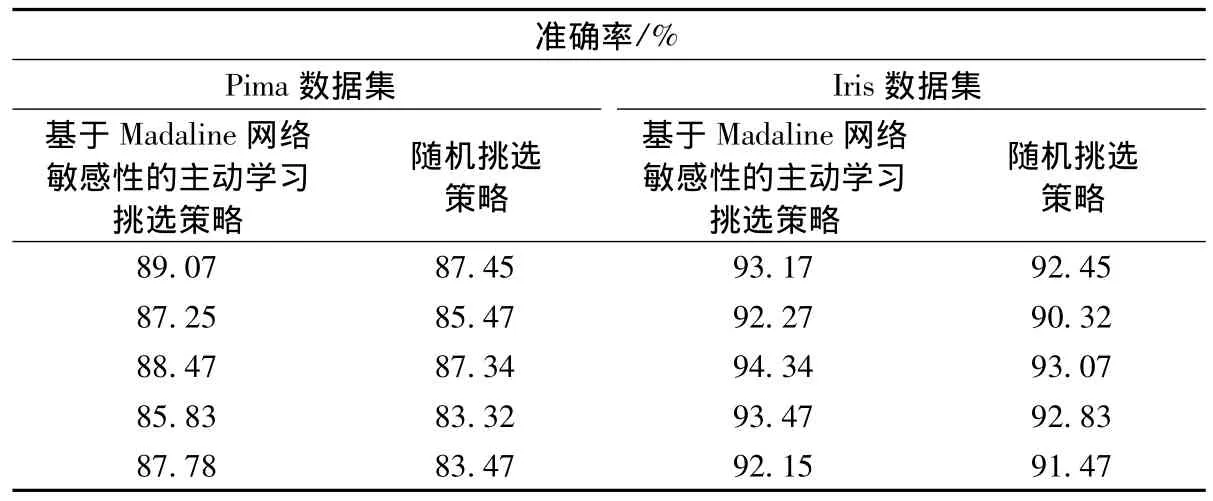
表1 基于Pima数据集和Iris数据集2种挑选策略实验结果Table 1 Experimental results of two methods based on Pima and Iris datasets

5 结 语

针对如何从大量的未标注数据样本中挑选最有价值的样本进行学习问题，本文提出了一种基于Madaline网络敏感性的主动学习算法。算法的核心是打造一种合适的Madaline网络敏感性尺度，有的放矢地选择需要的训练样本，从而实现主动学习的功能。实验结果验证了基于Madaline网络敏感性主动学习算法的有效性和可行性。

［1］赵秋焕.两种主动学习方法［D］.石家庄:河北大学，2010.

［2］崔宝今.基于半监督和主动学习的蛋白质关系抽取研究［D］.大连:大连理工大学，2008.

［3］FREUND Y，SEUNG H S，SHAMIR E，et al.Selective sampling using the query by committee algorithm［J］.Machine Learning，1997，28(2/3):133-168.

［4］DAGON I，ENGELSON S.Committee-based sample selection for probabilistic classifiers［C］//Proceedings of 12th Int’l Confon Machine Learning.San Francisco，CA:Morgan Kaufmann，1995:150-157.

［5］ARGAMON-ENGLESON S，DAGAN I.Committee-based sample selection for probabilistic classifiers［J］.Journal of Artificial Intelligence Research，1999，11:335-360.

［6］LEWIS D D，GAIL W A.A sequential algorithm for training text classifiers:corrigendum and additional data［J］.Sigir Forum，1995，29(2):13-19.

［7］MCCALLUM A K，NIGAM K.Employing EM and pool-based active learning for text classification［C］//Proceedings of the Fifteenth International Conference.Madison，WI，USA:Morgan Kaufmann Publishers，1998:350-358.

［8］MUSLEA I，MINTON S，KNOBLOCK C A.Active learning with multiple view［J］.Journal of Artificial Intelligence Research，2006，27:203-233.

［9］RUMELHART D E，HINTON G E，WILLIAMS R J.Learning representations by back propagation errors［J］.Nature，1986，323: 533-536.

［10］RUMELHART D E，MCCLELLAND J L.Parallel distributed processing:explorations in the microstructure of cognition，vol.l［M］.Cambridge:MIT Press，1986.

［11］WINTER R，WIDROW B.Madaline ruleⅡ:a training algorithm for neural networks［C］//IEEE International Conference on Neural Networks.San Diega，CA，USA:IEEE Publishrs，1988:401-408.

［12］WINTER R.Madaline ruleⅡ:a new method for training networks for Adalines［D］.Stanford:Standford University，1989.

［13］ZHONG Shuiming，ZENG Xiaoqin，WU Shengli，et al.Sensitivity-based adaptive learning rules for BFNNs［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23(3):480-491.

［14］曾晓勤，何嘉晟.单隐层感知机神经网络对权扰动的敏感性计算［J］.河海大学学报:自然科学版，2013，41(4):360-364. (ZENG Xiaoqin，HE Jiasheng.Computation the sensitivity of perceptrons with one hidden layer to weight perturbation［J］. Journal of Hohai University:Natural Sciences，2013，41(4):360-364.(in Chinese))

［15］WANG Yingfeng，ZENG Xiaoqin，YEUNG D，et al.Computation of Madalines’sensitivity to input and weight perturbations［J］. Neural Computation，2006，18(11):2854-2877.

［16］ZHONG Shuiming，ZENG Xiaoqin，LIU Huiyi，et al.Approximate computation of Madaline sensitivity based on discrete stochastic technique［J］.Science China:Information Science，2010，53(12):2399-2414.