区调扇区重构的指派模型和算法

叶志坚，孟令航，耿增显

（中国民航大学天津市空管运行规划与安全技术重点实验室，天津 300300）

区调扇区重构的指派模型和算法

叶志坚，孟令航，耿增显

（中国民航大学天津市空管运行规划与安全技术重点实验室，天津 300300）

为有效适应交通需求在时间和空间上的变化，在功能区块航空器数量量化和采用多管制员团队的基础上，提出了一种适应性区调扇区重构的指派模型和算法。对目标空域作网格处理，统计得到每个网格的航空器平均分布数量。航空器分布数量系数被用来修正管制员进行协调、移交和解决冲突的额外工作负荷，修正后的航空器分布数量影射到每个网格。设计了网格分组的多时段、变人数、变处理能力背包指派模型和计算方法。数值实例显示模型可行，算法有效；随模拟空域范围变大，人力资源需求有明显减少的趋势；在空域范围较大且日需求较高时，指派算法得到的结果比当前3个班组轮班使用的人力资源需求减少15%左右；在日交通需求较低时，指派算法也能达到比当前3个班组轮班使用的人力资源需求减少8%的效果。

空域规划；适应性扇区划分；安全性；管制员工作负荷；监控警告参数

随着中国经济和民航事业的发展，终端和航路通行能力得到改善，流量进一步增加，飞行流量较大地区的管制员面临更严峻的、超负荷工作的挑战，为了缓解这一矛盾，中国民航在多个地区实施了流量管理协同决策并取得了较好的效果。但从构建新一代空中交通管理系统的角度分析，还需解决一些配套问题。为了化解交通需求和空域通行能力不平衡的矛盾，根据国外的经验，一是通过流量管理措施，限制高峰时段的需求或改航改变交通流地理分布，平峰消谷；二是动态空域配置，增大空域通行能力并减少延误，如增开扇区以减少管制员工作负荷，扇区重构以适应随时空变化的交通需求，动态边界调整以适应改航需求，扇区合并以减少交通低谷时段人力资源浪费等[1]。由于目前中国航路空域容量已趋于饱和，对扇区重构和增开扇区的需求越来越迫切，扇区重构与管制员指派的联合优化是解决问题的关键。

最近几年关于指派问题算法的研究成果颇多，王立柱研究的是（m，n，k）指派问题[2]，孙晓雅提出使用蚁群算法来求解标准指派问题[3]，熊德国用网络流理论来求解标准指派问题[4]，费威在其博士论文中采用最小调整法来求解标准指派问题[5]，李岩研究了个人能力不同的任务指派问题[6]。这些模型和空域块指派模型有很大的不同，车辆组合问题、车辆装载能力是线性叠加的，而管制员人数组合处理航空器能力不是线性叠加的，另一个区别在于后者非一次性指派，而是多时段指派问题。本文研究的是多时段、变人数、变处理能力的空域指派问题及其求解。

1 交通流地理分布网格化处理

1.1 网格内航空器平均分布数量处理

对整个目标空域交通流地理分布做离散化处理：将包括有整个目标空域的航路航线图按10 km间隔一条经线和一条纬线划经纬线网格，并对每个网格编号为Gi，i=1，2，…，n；凡是有航路航线经过的网格都做航空器分布数量量化处理。对应于一个扇区计划时间段[T0，T1]，一般按24 h处理，统计该时间段内：

1）飞经每个航段routex（x=1，2，…，k）的航空器架次 Nroutex；

2）小时平均数量即流量（架次/h）为

其中：lGi为航段在网格Gi中的长度；σ为网格内航空器数量系数；σ取决于管制员日常任务次数、处理冲突次数和所需要的处理时间。网格所处的不同位置决定了这些事件是否在网格内发生，一旦发生则需要考虑其对管制员带来的影响。

1.2 网格内航空器数量系数量化

网格内航空器数量系数量化主要考虑客观工作负荷，即由日常事件造成的负荷增加和特殊事件造成的增加，网格内航空器数量系数量化表达式为

其中：36是扇区内平均每架航空器所需处理时间（s）[7]。

1.2.1 日常事件发生地点的航空器数量系数量化

日常事件发生地点的航空器数量系数量化和发生频率、处理时间有关。在扇区入口点或出口点有以下日常事件：管制员和管制员协调、管制员和飞行员确认接管[8]；在转弯点或强制报告点的日常事件：监控；在扇区内任意点：飞行员请求、指出或点选、管制员对交通结构的情景意识构建。日常事件在一个扇区中出现的频率和处理时间及发生地点根据现场观察，如表1所示。

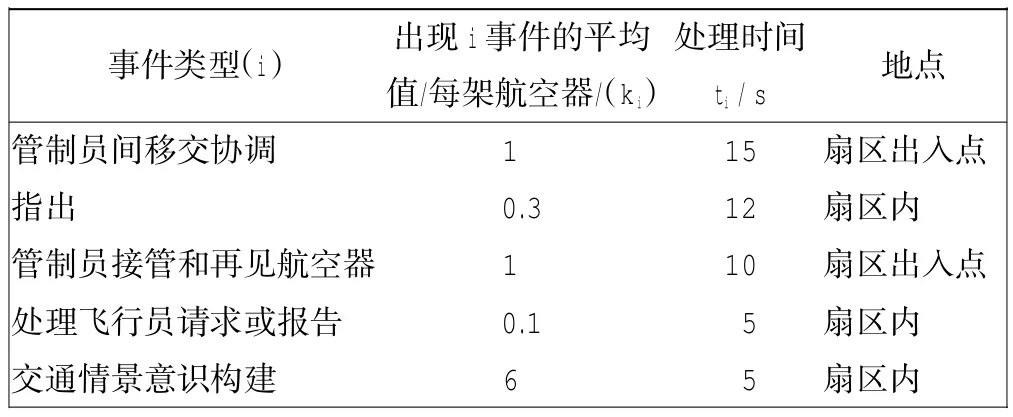
表1 日常事件平均频率及处理时间Tab.1 Mean frequency and dealing time of daily event

1）在扇区入口点或出口点

σ=[（15+10）/36+0]+1，其意义是在扇区入口点和出口点，每架航空器相邻扇区管制员之间必须协调一次，处理时间是15 s，管制员和飞行员必须通话一次，处理时间是10 s，而航空器在扇区内平均处理时间是36 s，则

入口点网格处量化航空器数量=实际分布航空器数量×α=实际分布航空器数量×[（25/36）+1]

2）强制报告点或转弯点

σ=[（5/36）+0]+1，其意义是在强制报告点或转弯点，每架航空器需要管制员必须处理1次，处理时间是5 s，而航空器在扇区内平均处理时间是36 s，则

强制报告点或转弯点网格处量化航空器数量=实际分布航空器数量×[（5/36）+1]

3）除扇区入口点或出口点、强制报告点或转弯点，交叉点外的其他位置点，可能出现的事件是“指出”、“处理飞行员请求”、“交通情景意识构建”，这些事件在网格内可能发生也可能不发生，发生的概率表达为

其中：lGi是在网格内航路段的总长度，平均速度为800 km/h；（lGi×60/800）是航空器在网格Gi内用分钟表示的飞行时间；11 min是1架航空器在扇区内的平均飞行时间。在任意一个这样的网格内上述日常任务处理次数为

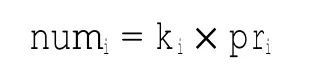
处理总时间为

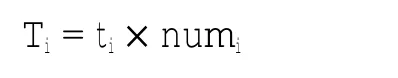
网格处量化航空器数量=实际分布航空器数量×

1.2.2 特殊事件发生地点的航空器数量系数量化

特殊事件特指交叉冲突，在交叉点出现，交叉点航空器数量系数量化与潜在冲突次数和处理时间相关。

航路交叉点潜在冲突事件次数可以表达为流量、沿航路速度、最小所需间隔，及冲突可能存在的航路间交叉角和飞行高度层数量的函数。函数关系为[9]

其中：Econflict是每小时平均交叉冲突数量，有n个可用高度层；过交叉点有m个两两航路交叉；fi1是在i高度层沿航路1的流量；fi2是在i高度层沿航路2的流量；X是航空器纵向间隔标准；Vi1是在i高度层沿航路1的航空器飞行速度；Vi2是在i高度层沿航路2的航空器飞行速度；α是两两交叉航路交叉角。冲突处理时间根据现场观察按60 s计算。

1.3 交叉点邻域打包

为保证交叉点与划分的扇区边界有足够的距离，为管制员做冲突调配留下足够余地，交叉点附近邻域和交叉点本身必须在一个扇区，交叉点距离小于30 km的也必须在一个扇区，即由一个货郎来打包处理。航空器进入扇区需要移交，移交完毕如果有冲突，必须有足够时间解决冲突，移交时间包括管制员听飞行员报告加发指令时间，接近20 s，解决一次冲突时间为50 s，总计不超过1.5 min，预留2 min为交叉点距离边界的安全飞行时间，民航飞机航路平均飞行速度大约0.8个马赫数，接近800 km/h，2 min飞行距离27 km，相当于3个网格的距离，2个交叉点距离小于30 km的也合并在一个区块。这些区块都在一个扇区，就可以保证管制员有充分时间完成移交和解决冲突。

假设通过处理后有m个区块，区块数学描述为

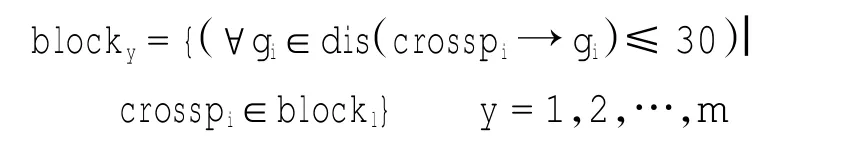
其处理数量为各个网格处理数量之和。

2 扇区划分背包指派模型设计

2.1 指派路径

从目标空域指定的入口点开始，遇见交叉点顺时针转出，走完转出路径，再次转入，如此反复得到如图1所示带箭头的虚线，即走行路径。对每个走行路径经过的网格重新编号，即gi，i=1，2，…，n；交叉点处区块（交叉点附近邻域）编号按一个网格处理。

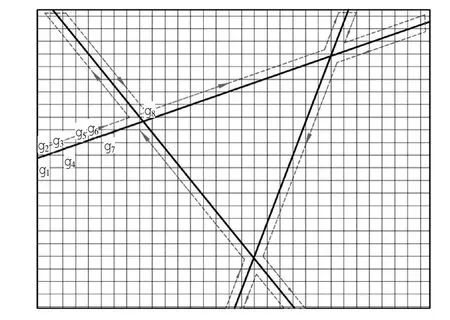
图1 指派顺序路径示意图Fig.1 Assignment sequence path diagram

网格重新编号处理完后，得到一个功能区块指派顺序字符串链{g1，g2，…，gn}。将g1和gn相连，得到一个环状链，如图2所示。

2.2 时段确定

首先根据有相似特性的历史统计数据预测未来24 h之内的小时流量，作流量（架次/小时）分布图，共3条线，分别为日流量均值线、日流量均值加标准偏差线和日流量均值减标准偏差线。

时段划分方法1 把未来24 h划为2个时段，以日流量均值线上方的合并为1个时段，日流量均值线下方的合并为1个时段，即08：00—19：00/19：00—08：00/，1个时段工作时长11 h，另一个时段长13 h。为公平起见，把第一个时段往后延长1 h，即08：00—20：00/20：00—08：00，这样2个时段长度都为12 h。

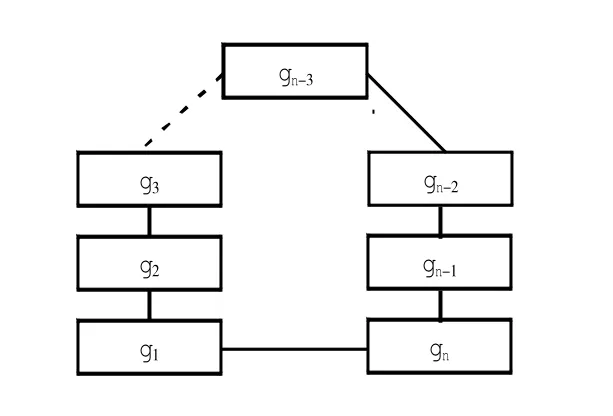
图2 指派顺序字符串链Fig.2 Assignment sequence string chain

时段划分方法2 把小时流量高于日流量均值加标准偏差线的时点合并为一个时段；把小时流量低于日流量均值加标准偏差线，且小时流量高于日流量均值减标准偏差线的时点合并为一个时段；把小时流量低于日流量均值减标准偏差线的时点合并为一个时段。时段划分过多，工作时段过短，需轮班的班组增加，人力成本上升；时段划分过少，工作时段过长，管制员易疲劳，安全得不到保障。如图3所示，是一个典型的24 h流量及均值分布图，根据以上所述，把未来24 h划为3个时间段，即00：00—08：00/08：00—16：00/16：00—24：00。

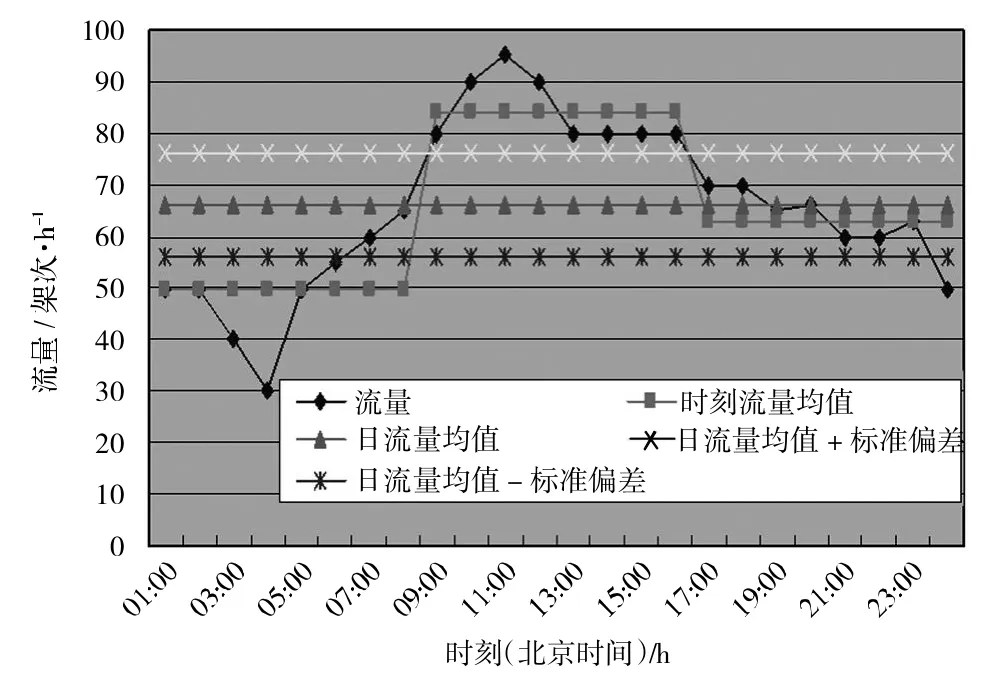
图3 日流量及均值分布Fig.3 Distribution of daily flow and mean

时段划分方法3 在方法2的基础上，将3个时段再次均分，得到6个时段，即00：00—04：00/ 04：00—08：00/08：00—12：00/12：00—16：00/16：00—20：00/20：00—24：00。时段数量用τ表示，τ的取值是2、3、6。

2.3 确定每个时段每个功能区块航空器数量分布

统计每个功能区块15 min内高峰瞬间计数，以8 h时段为例有32个计数，取其平均值得到区块航空器数量分布对所有时段的全部功能区块做相似处理，得到功能区块航空器数量分布矩阵

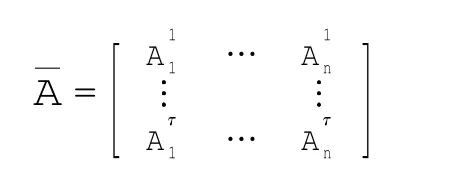
2.4 背包指派模型

K（j=1，2，…，k）个扇区，k未知；n个功能区gi，i= 1，2，…，n；3个时间段t=1，2，3；目标是用最少的人力资源将n个功能区指派给k（k未知）个扇区。1个扇区2个管制员的监控警告参数设为17，1个扇区1个管制员的监控警告参数设为12，该参数设置是参照美国联邦航空局1997年关于雷达管制人员配备标准研究报告设定的[10]。取MAP=17意味每个扇区需要配备2个管制员，按这个参数设计的扇区比按MAP=12（目前中国无论扇区管制员人数多少，区调都用这个标准）设计的扇区更大，比按MAP=29（3个管制员）设计的扇区更小。扇区设计足够大，每个管制员熟悉的空域范围大，便于边界动态调整时减小管制员的不适应；扇区如果按3个管制员来设计，扇区能保证足够大，但交通流急剧增加时无法通过增加管制员来分解工作负荷，将增加运行安全风险；在交通量较小时，可通过减少管制员配置来运行，减少了频繁合扇的概率，提高了安全性。因此，在设计阶段管制员配置时最多配置2个，交通流变化时，通过增减管制员数量来解决，可以节约人力资源，并提高安全性和适应性。通过指派组合功能区，将空间工作负荷限定在监控警告参数以下，组合的功能区在τ个时段保持不变，减少扇区边界频繁变动，以人数增减来适应不同时段τ交通需求随时间的变化，目标函数是使用的总管制员数量最少。

指派模型：包括目标函数和约束。目标函数为

其中：t是划分的时间段序号；τ是时段数量；j是扇区序号；k是扇区数量表示t时段内j扇区使用的管制员数量。约束为

3 遗传算法设计

3.1 背包法求（p＞20）个初始可行解

由于按监控警告参数=12来设计扇区，大趋势上比按监控警告参数=17更节约人力资源，故求初始解按监控警告参数=12作为背包上限，相应的扇区人员按1个来配置。这是一个标准指派问题，可用解模型2的方法[2]来求最优解，为了简化计算，这里只需要可行解，故采用货郎背包法。

Mj是货郎实际背负的值。从第1个进入点开始沿航路顺时针方向背货，背到不能背为止，背负的负荷小于等于监控警告参数。假设走行步数用ξ表示，除了交叉点必须一步走完，其余都是一步一个网格，遇见第y个交叉点邻域在第ψ步，能背负就装上，沿顺时针从包块出去围绕包块直到装满；若不能背负从包块顺时针出，到边界后顺时针进入下一个网格。如此反复，直到这里的y是最近一个交叉点下标。

解表达形式：

1）字符串编码形式，如图4所示。

2）程序中用集合表示，用于遗传操作

g1和gn相邻，g4和g5相邻，依此类推，每个集合的最后一个元素与下一个集合的第1个元素相邻，形成一个闭环形式，如图4所示。

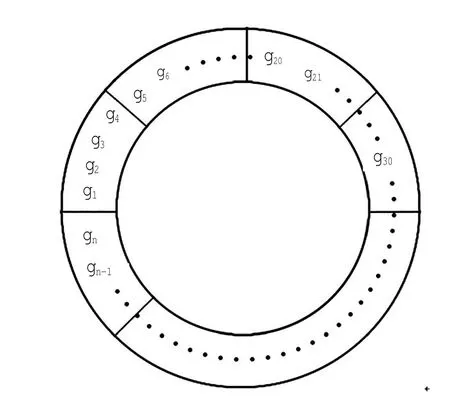
图4 字符串编码解表达形式Fig.4 String encoding solution

再以其他进入点和交叉点为开始点沿航路顺时针方向背货，如果以其他进入点和交叉点为开始点产生的可行解不足p个，则以2个交叉点的中点作为开始点生成可行解，所有按上述步骤产生p个可行解{φ1，φ2，…，φp}。

3.2 适应度函数

目标函数是最小化问题，适应度函数为

3.3 选择

用蒙特卡罗法，第z个解被选中的概率为

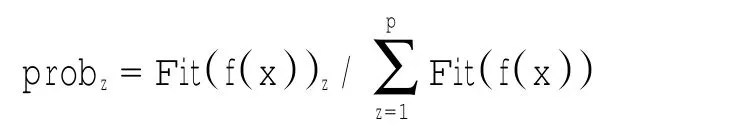
3.4 交叉

交叉模式

|代表交叉点位置，交叉操作采用贪婪搜索。第1次交叉，交叉点在g1、g2之间；第2次交叉，交叉点在g2、g3之间；依此类推，有n-1次交叉，产生2（n-1）个子代。将满足适应度函数者送入解数据库，每送1个，p+1，在交叉操作结束后更新probz。

3.5 变异

{1，2，3，4}{5，6，7}{8，9，10，11，12}…{…n}的变异模式。

采用以下2种变异模式，产生6个孙代：

1）元素右移变异

a.元素右移一步变异：{2，3，4，5}{6，7，8}{9， 10，11，12}…{…n，1}孙代

b.元素右移二步变异：{3，4，5，6}{7，8，9}{10， 11，12，13，14}…{…n，1，2}孙代

2）双集合拔河变异

随机选择sk，如选到s2

c.s2增长1个元素，{1，2，3，4}{5，6，7，8，}{9， 10，11，12}…{…n}；孙代

d.s2增长 2个元素，{1，2，3，4}{5，6，7，8，9} {10，11，12}…{…n}；孙代

e.s2减少1个元素，{1，2，3，4}{5，6}{7，8，9， 10，11，12}…{…n}；孙代

f.s2减少2个元素，{1，2，3，4}{5}{6，7，8，9， 10，11，12}…{…n}；孙代

将满足适应度函数的孙代送入解数据库，每送一个，p+1，在变异操作结束后更新probz。

3.6 终止条件

使用如下终止条件：

1）定义最大遗传代数genmax，若达到最大遗传代数则结束；

2）从第gens代开始比较，若连续ω代Fit（f（x））没有明显的改善则结束。

4 实验结果及分析

采用某区调300×300 km2、600×600 km2、900× 900 km2、1 200×1 200 km2、1 800×1 800 km2共5个空域范围在需求较高繁忙日统计数据，用前述的模型和方法做了模拟试验。图5是不同空间范围减少人力资源需求的对比，结果显示在空间范围小于900× 900 km2联合优化结果不敏感，差异不大，随模拟空域的增大，优化效果有逐渐增加的趋势。产生这种差异化效果的主要原因是在空域范围较小时，交通流地理分布差异不大，因此优化结果不明显；在空域范围较大时，交通流时空分布的不均衡性比较明显，能得到较明显的优化结果。

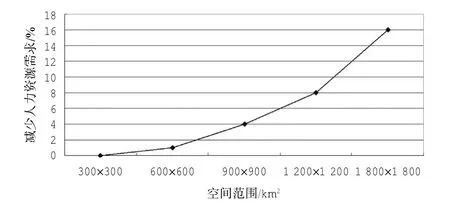
图5 人力资源需求对比Fig.5 Comparison of human resource demand

表2为1 800×1 800 km2空域范围内2日需求状况下，采用不同时段长度的管制员需求对比结果。从结果来看，日需求较高，节约使用的管制员数量越多，日需求较低，节约使用的管制员数量越少；划分时段数量少，管制员日工作时间长，管制员需求也少。从节约人力资源使用角度看，希望管制员工作时间越长越好，但过长的工作时间会增加管制员疲劳的风险；划分时段数量多，管制员日工作时间短，管制员需求也多，会增加人力资源使用成本。1日分3个时段是现在各管制室常用的时段划分法，在τ=3时，对比两种交通需求模式发现，在日需求变化较高时，使用本文模型计算，能比同样按3个时段排班的当前人力资源节约15.8%，在日交通需求较低时，也能达到8%的节约。

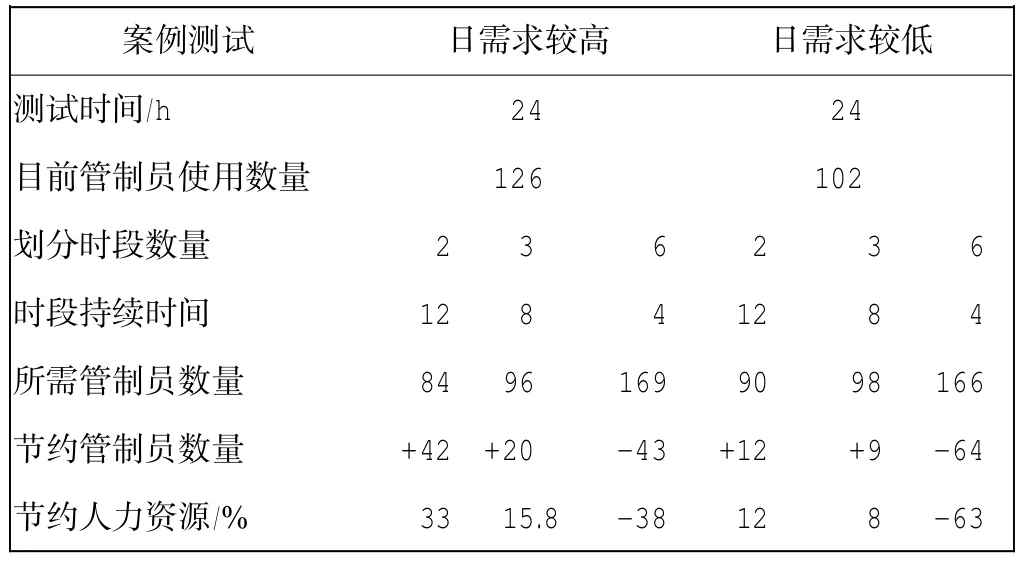
表2 管制员需求数量对比Tab.2 Comparison of controller demand

5 结语

本文从中国非自由飞行实际情况出发，采用坐标网格粒度化地理空间，用航空器数量系数和网格内航段长度量化网格内航空器平均分布数量，航空器数量系数考虑了不同网格地理位置管制员可能增减的工作负荷，增加的负荷包括协调、接管、监控、解决冲突和移交，并给出了量化方法。将空域扇区划分与人力资源管理联合优化，抽象成多时段、变人数、变处理能力的空域指派问题并求解。数值实例显示该法适应性较强，留有可进一步增加人手解决峰值超负荷问题的空间，扇区结构在计划时间前变动，在计划时间范围内的各个时段，扇区结构保持不变，避免了扇区频繁变动带给管制员的不适应，增加了区调扇区解决交通需求时空分布不均衡问题的灵活性和安全性；在空域范围较大、时空分布不均衡条件下，使用建立的模型和算法对减少管制员使用数量有效且可行。2个班组轮班虽能明显减少人力资源使用，但管制员单班工作时间过长，隐藏安全风险，不建议使用；采用4 h一个班的轮班制，人力资源使用显著上升，不适合当前管制员紧缺的现状；保持目前三班倒的轮班制度，且根据需求动态增减人数使用是个好的选择。使用遗传算法和贪婪搜索相结合，解决了处理能力随人数增长的背包指派寻优问题。

[1]ARASH Y，BABAK K，GIRISHKUMAR S，et al.Effectiveness of Dynamic Airspace configuration to Manage Airspace Capacity in Response to Highly Dynamic Changes in Traffic Demand and Weather Events[C]// 10th AIAA Aviation Technology，Integration，and Operations（ATIO）Conference，Fort Worth，Texas，2010：1-9.

[2]王立柱，刘 阳.分配小于人数和任务数的指派问题的反点算法[J].运筹学学报，2011，15（3）：124-128.

[3]孙晓雅，林 焰.改进的人工蜂群算法求解任务指派问题[J].微电子学与计算机，2012，29（1）：23-26.

[4]熊德国，胡勇文.用最小费用流的允许边算法求解指派问题[J].山东大学学报（理学版），2012，47（3）：103-109.

[5]费 威.最小调整法的改进及其在经济优化中的应用[D].大连：东北财经大学，2010.

[6]李 岩，郭 强.非确定型指派问题的求解算法[J].计算机工程与应用，2009，45（15）：61-66.

[7]ROBERTO Arca Jaurena.Guide for the Application of a Common Methodology to Estimate Airport and Atc Sector Capacity for the SAM Region[R].Lima，Peru，ICAO RLA，2009.

[8]项 恒，赵嶷飞.空中交通管制员工作任务分析[J].中国民航大学学报，2007，31（4）：31-34.

[9]SIDDIQEE W.A mathematical model for predicting the number of potential conflict situationsat intersecting air routes[J].Transportation Science，1973，7（2）：158-167.

[10]JO7210.3v，Facility Operation and Administration[S].FAA，2008.

（责任编辑：党亚茹）

En route sector reconstructing assignment model and algorithm

YE Zhi-jian，MENG Ling-hang，GENG Zeng-xian
（ATM Operation Planning and Safety Techniques Ley Kab of Tianjin，CAUC，Tianjin 300300，China）

In order to effectively adapt to traffic demand changes in time and space，based on quantization of the aircraft number in the function block and multi-ATC team，an adaptive sector reconfiguration assignment model and an algorithm are proposed.When the target airspace has been processed as grid，statistics of the evenly distributed aircraft number are obtained in each grid.Aircraft distribution coefficients are used to correct the extra workload while air traffic controllers conduct coordination，transferring and resolving conflicts.Then the amended aircraft distribution numbers are alluded to each grid.A backpack assignment model and calculation method is designed for grid grouping on condition of multi-period，variable job number and variable capacity.Numerical examples show that the model is feasible as while as algorithm is effective.On high demand day，assignment algorithm results reduce about 15%of human resource needs than current needs under three crew shifts.On low traffic demand day，the assignment algorithm results still can reduce about 8%of human resources needs.

airspace planning；adaptive sector division；security；controller workload；monitor alert parameter

V355.1

：A

：1674-5590（2014）04-0009-06

2013-06-26；

：2013-09-04

中国民用航空局科技基金（MHRD201014）；国家自然科学基金项目（61179042）；中国民航大学科研启动基金（05qd07s）；中央高校基本科研业务费专项（3122014C023；3122014D038）；国家空管委科研课题（GKG201405002）

叶志坚（1972—），男，贵州六盘水人，讲师，博士，研究方向为空中交通规划与管理.