具有直觉模糊信息的任务指派问题研究

孙晓雅

（辽宁师范大学 管理学院，辽宁 大连 116029）

指派问题是运筹学中的一类经典问题，属于特殊的0-1整数规划问题，它在工作安排，车辆调度、机器配置等生产与经营活动中都有重要应用。标准的指派问题是指在效益矩阵精确已知的条件下，确定n个人完成n项工作的最佳指派方案。在指派问题的求解方法中，匈牙利法因其求解的精确性和高效性被广为采用。

在实际问题中，指派问题的效益矩阵往往不能精确得到，更多的时候效益矩阵具有模糊性和不确定性，因此，近年来这类模糊指派问题得到了国内外学者的关注。Lin和Wen[1]提出了一种效益矩阵为区间模糊数的指派问题的标记算法。Yaakob和Watada[2]针对模糊方法求解指派问题，探讨了社会和心理因素的工人配置模型。张肃[3]等人提出出了一种区间数型的多因素指派模型的求解方法，并应用于多传感器的优化分配中。樊治平等人[4]和王坚强等人[5]将语言评价信息转换为模糊数，求解了效益矩阵为语言评价信息的群指派问题。

19世纪80年代Atanassov[6-7]对 Zadeh的模糊集理论进行了拓展，提出了直觉模糊集理论。直觉模糊集考虑了隶属度、非隶属度和犹豫度三方面信息，它比传统的模糊集更细腻地描述和刻画了客观世界模糊的本质[8]。关于具有直觉信息的指派问题的研究目前还不多见。在人员选拔和员工录用等指派情形下，企业常会采用投票或表决的方式来对员工是否适合担任某项工作进行评价选拔。这种情况下，指派问题的效益矩阵就需要用直觉模糊数矩阵的形式表达，本文将对这类具有直觉模糊信息的指派问题进行探讨。

1 直觉模糊的概念和比较排序方法

1.1 直觉模糊的定义

定义 1[6-7]设X是一个非空集合，则称A={＜x，uA（x），vA（x）＞|x∈X}为直觉模糊数，其中uA（x）和vA（x）分别为X中，元素x属于A的隶属度和非隶属度，即

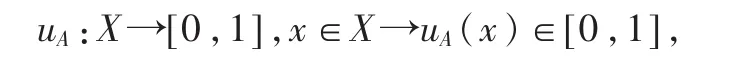
vA：X→[0，1]，x∈X→vA（x）∈[0，1]，且满足条件 0≤uA（x）+vA（x）≤1，x∈X。

此外 πA（x）=1-uA（x）-vA（x），x∈X表示X中，元素x属于A的犹豫度或不确定度。

定义2[9]X中的元素x属于A的隶属度与非隶属度组成的有序数对 α=（uα（x），vα（x））称为直觉模糊数。 其中uα∈[0，1]，vα∈[0，1]，uα+vα≤1， 且设 Θ 为全体直觉模糊数的集合。

1.2 直觉模糊的比较排序方法

定义 3[9-10]设 α1=（uα1（x），vα1（x））和 α2=（uα2（x），vα2（x））为 直 觉 模 糊 数 ，s（α1）=uα1（x）-vα1（x）和s（α2）=uα2（x）-vα2（x） 分别 为 α1和 α2的得 分值 ，h（α1）=uα1+vα1h（α2）=uα2+vα2分别为 α1和 α2的精确度，则

若s（α1）＜s（α2），则 α1小于 α2，记为 α1＜α2；

若s（α1）=s（α2），则

（1）若h（α1）=h（α2），则 α1和 α2相等 ，即uα1=uα2和vα1=vα2，记为 α1=α2；

（2）若h（α1）＜h（α2），则 α1小于 α2，记为 α1＜α2；

（3）若h（α1）＞h（α2），则 α1大于 α2，记为 α1＞α2。

2 直觉模糊指派问题建模与求解

2.1 标准指派问题的描述

指派问题的标准形式（以人和任务为例）：设有n个人和n项任务，已知第i人完成第j任务的费用为Cij（i，j=1，2，…，n），要求一个人和任务之间一一对应的指派方案，使完成这n项任务的总费用最少。

一般称矩阵

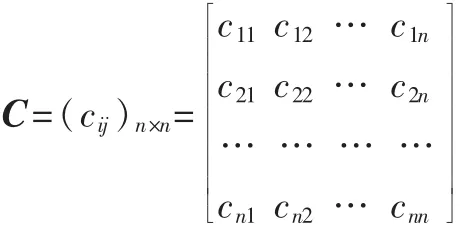
为指派问题的系数矩阵，或效益矩阵。

为了建立标准指派问题的数学模型，引入n2个0-1变量

（i，j=1，2，…，n）

这样，问题的数学模型可写成Model1的形式。

对于非标准指派问题，通常是先将非标准型转化为标准型，然后就可以按标准指派问题进行求解。

2.2 直觉模糊指派问题

具有直觉模糊信息的指派问题是指效益矩阵为直觉模糊数矩阵。对于有n个人和n项任务的指派问题，效益矩阵=（）n×n，（i，j=1，2，…，n）。（uij，vij）表示第i人做第j任务的直觉模糊数，其中uij代表第i人做第j项任务的赞成率，vij代表第i人做第j项任务的反对率。如一个指派问题，有10个人投票表决，其中23=（0.6，0.3），则表示对于第2个人做第3项工作有6人赞成，3人反对，1人弃权。

具有直觉模糊信息的指派优化目标是完成各项工作支持票越多越好，反对票越少越好。基于这一思想可以得到一个多目标优化问题的数学模型，如Model2所示。

将上面多目标数学模型中将赞成和反对按相等的权重进行考虑，则转化为单目标0-1优化问题，如Model3所示。

可以看出，Model3已经转化为效益矩阵为直觉模糊数的得分矩阵的最大化指派问题。

2.3 具有直觉模糊信息的指派问题求解步骤

具有直觉模糊信息的指派问题求解分为如下步骤：

（3）如果将矩阵分为非标准指派矩阵，并将非标准问题转化为标准指派问题，利用匈牙利方法求解效益矩阵为直觉模糊数的得分矩阵的指派问题Model3。Model3的最优解即最优指派方案。

3 实例研究

某一员工选拔的问题中，有6项重要任务，需要在10名员工中选拔6人分别完成其中一项任务。员工选拔通过专家投赞同和反对票的形式来决定，得到直觉模糊矩阵如表1所示。

由表1直觉模糊矩阵，求得得分值矩阵如表2所示。

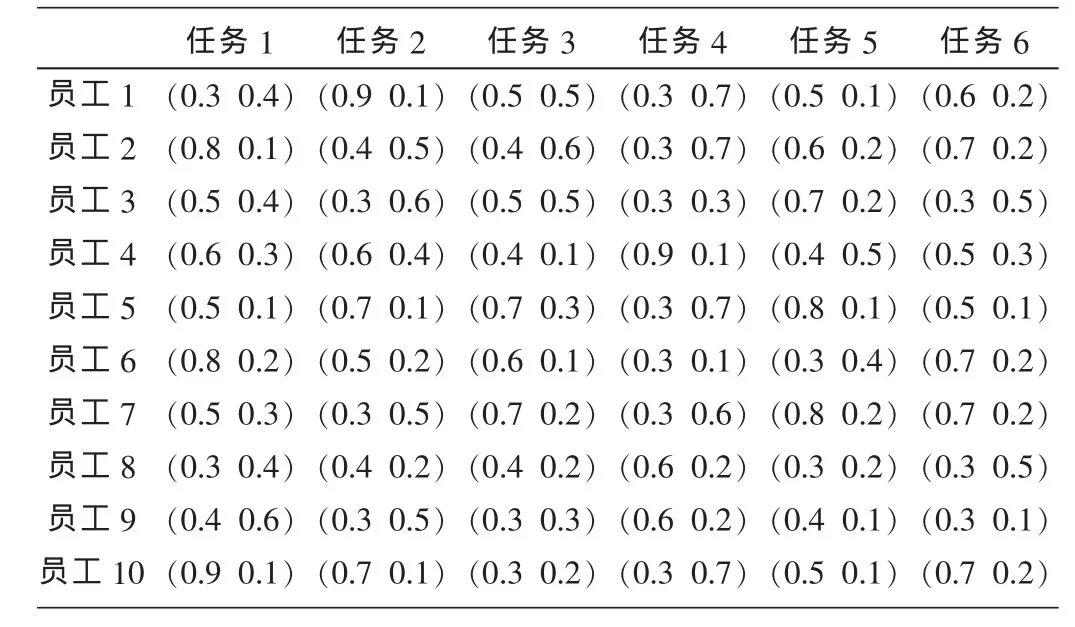
表1 员工完成各项任务的直觉模糊数矩阵

本问题是一个人多任务、目标函数最大化的非标准指派问题，将得分矩阵做为效益矩阵，求解该非标准指派问题得到的最优指派方案如表3所示。

结合模糊直觉数矩阵，可以看出通过表3的指派方案选拔出的6名员工，分别去执行各自的任务将会是大家赞同率最高，反对率最低的最优化指派结果。另外，员工3、7、8、9由于支持率不高，反对率较大，不安排执行任务。

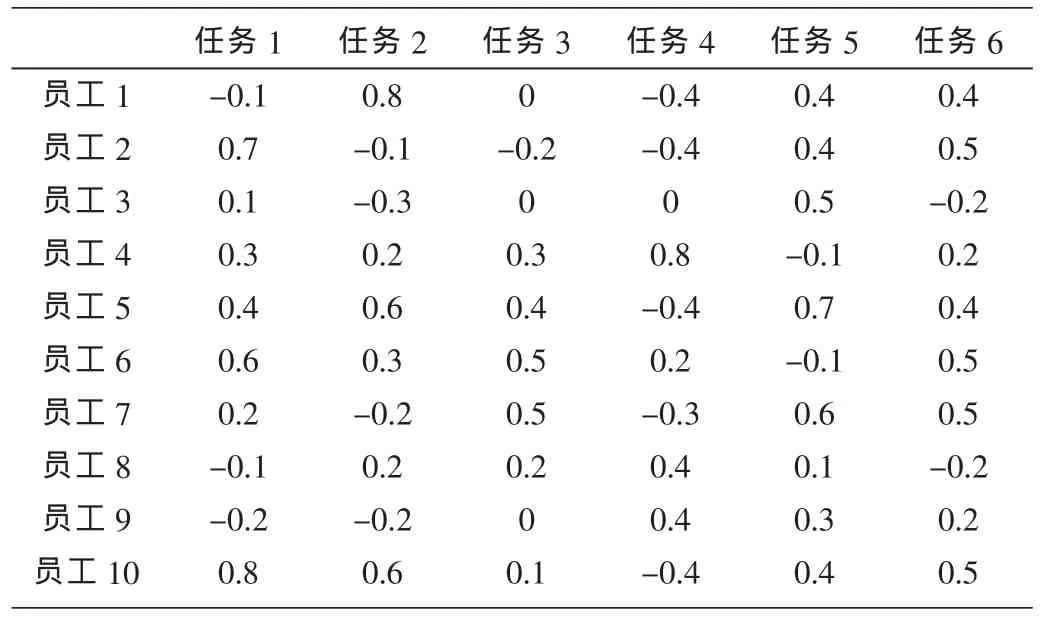
表2 员工完成各项任务的直觉模糊数得分值矩阵

表3 最优指派方案

具有直觉模糊信息的指派问题是一类常见的真实指派问题，本文建立了的直觉模糊指派问题的数学模型，并探讨了数学模型的求解方法。得到以下两点结论：（1）在人员选拔，任务安排和机器资源等配置的指派问题中，采用直觉模糊数的进行决策的方法更具客观性，它反映了隶属度，非隶属度和犹豫度三方面的信息，使得指派方案的评价更细致、更科学。（2）实例计算表明，本文将直觉模糊的指派问题转化为以得分值矩阵为效益矩阵的最大化指派问题进行求解，该方法简单、有效、易于操作。综上，本文所提出的直觉模糊指派问题符合实际需求且简便易行，适合在指派决策中推广应用。

[1]LIN C J，WEN U P.A labeling algorithm for the fuzzy assignment problem[J].Fuzzy Sets and Systems， 2004，142：373-391.

[2]YAAKOB S B，WATADA J.Fuzzy approach for assignment problem[C].IEEE International Conference on Fuzzy Systems，2009.

[3]张肃，程启月，申卯兴.基于区间数型多因素指派模型的多传感器优化分配方法 [J].自动化学报，2008，34（2）：240-245.

[4]樊治平，王欣荣.具有语言评价信息的指派问题求解方法[J].系统工程学报，2004，19（1）：14-19.

[5]王坚强，孙超.不完全确定信息的群体语言指派问题的求解方法[J].中国管理科学，2007，15（1）：74-79.

[6]ATANASSOV K.Intuitionistic fuzzy sets[C].In：Sgurev V ed.VII ITKR′s Session， Sofia， 1983.

[7]ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems， 1986（20）： 87-96.

[8]BUSTINCE H，BURILLO P.Vague sets are intuitionistic fuzzy sets[J].Fuzzy Sets and Systems， 1996， 79： 403-405.

[9]XU Z S，YAGER R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems， 2006， 35（4）： 417-433.

[10]XU Z S.Intuitionistic fuzzy aggregation operators[J].IEEE Transactions on Fuzzy Systems， 2007，15（6）：1179-1187.