投影算子的一种简单算法
2014-03-14何松年赵子祎
何松年,赵子祎
(中国民航大学理学院,天津 300300)
投影算子的一种简单算法
何松年,赵子祎
(中国民航大学理学院,天津 300300)
提出了投影算子的一种Halpern型的松弛算法,由于这种算法把计算关于一个凸函数水平集的投影转化为计算关于一列包含水平集的半空间的投影,因而算法容易实现,并且证明了算法的强收敛性。
投影;半空间;强收敛;Hilbert空间
设H是一实Hilbert空间,其内积与范数分别表示为<·,·>和‖·‖,C⊂H非空闭凸。从H到其非空闭凸子集C上的投影PC定义为:对于任意x∈H,必有C中唯一一点,记作PCx,满足

且PC有如下特征:对x∈H,有

投影算子在很多算法中都会涉及到:如不动点的求解,凸优化问题的求解,变分不等式[1]以及分裂可行性问题[2-5]的求解等。由于对一般闭凸子集C,投影算子PC没有显式表达式(除非C是闭球或者半空间等简单情形),所以投影算子的计算一般难以实现。
假设T:C→C为非扩张映像,其不动点集Fix(T)非空,众所周知Fix(T)闭凸的。计算T的不动点的Halpern迭代格式为

其中:u∈C取定,x0∈C任意取定,{λn}⊂(0,1)。关于Halpern迭代的收敛性,有如下基本结果:
定理1 设H是一实Hilbert空间,其内积与范数分别表示为<·,·>和||·||,C⊂H非空闭凸,T:C→C非扩张并且满足F(T)≠Ø,又设

则序列(xn)强收敛到PFix(T)u。
假设c:H→R为凸函数,本文讨论关于凸函数c的水平集投影的计算方法,其中水平集为
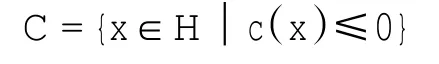
本文提出投影算子的一种Halpern型松弛算法,具体如下
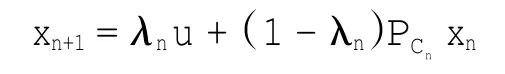
其中:取u∈H,任意取定初值x0∈H,Cn⊃C(n=1,2,…)是一列半空间(Cn的确切构造见第2节),由于这种算法是把计算关于一个凸函数水平集的投影转化为计算关于一列包含水平集的半空间的投影,所以此算法容易实现。将在第2节证明此算法产生的序列在一定条件下强收敛于PCu。
1 预备知识
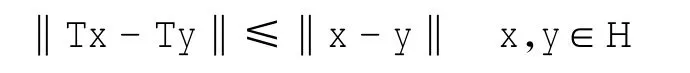
若成立:对任意的x,y∈H

则称T是firmly非扩张的。投影PC是一个典型firmly非扩张映像例子。
称元素g∈H为f:H→R在点x处的次梯度,如果有
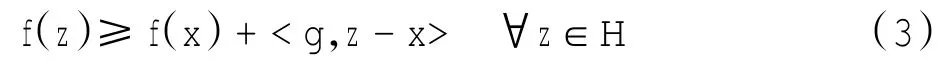
函数f:H→R如果在点x处至少有一个次梯度,则称函数f在点x处次可微,f在点x处的次梯度集称为f在点x处的次微分,记为∂f(x)。式(3)称为f在点x处的次微分不等式。如果对于∀x∈H,f在点x处都次可微,则称f是次可微的。
引理1 对于所有的x,y∈H,满足
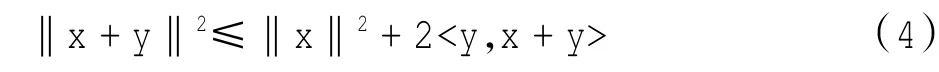
引理2 假设{sn}为非负实数列,且满足[6]
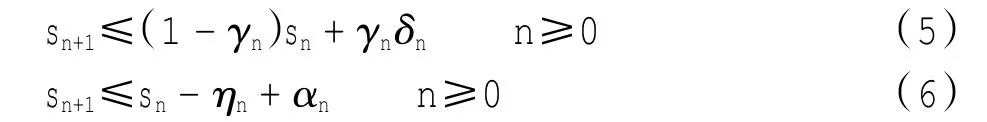
{γn}是(0,1)上的数列,{ηn}为一非负实数列,且{δn}和{αn}都是R上的数列,满足如下条件
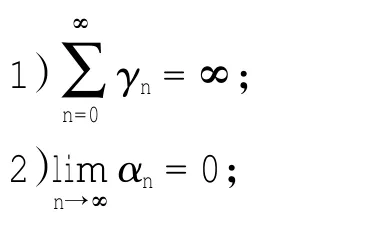
3)对任意的子列{nk}⊂{n},只要就有
引理3 T:H→H的一个算子,以下命题等价[7]
1)T是firmly非扩张的;
2)‖Tx-Ty‖2≤
3)I-T是firmly非扩张的。
2 迭代算法及其收敛性
本节给出本文算法并证明其收敛性。假设c:H→ R为一凸函数,总是假设c在H上是次可微的,并且∂c是有界算子(也就是在有界集上是有界的)。值得注意的是定义在有限维Hilbert空间中的每一个凸函数都是次可微的,并且其次可微算子是有界的[8]。假设算法第n步迭代xn已经得到,基于次微分不等式,构造如下半空间
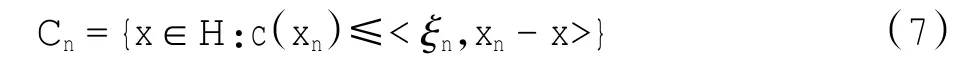
其中:ξn∈∂c(xn)。由次微分不等式容易验证Cn⊃C= {x∈H|c(x)≤0}。
算法1 取u∈H,任意初值x0∈H取定,(xn)以如下迭代格式产生
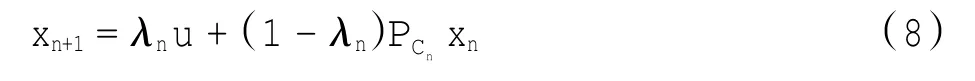
其中:Cn由式(7)给出,并且{λn}⊂(0,1)。
下面运用引理2来分析算法1的强收敛性。
定理2 假设λn→0(n→∞)并且由算法1产生的迭代序列(xn)强收敛于PCu。
证明先证明序列(xn)有界。
令PCu=z,由式(8)及引理1得

所以得证(xn)是有界的。
从式(9)的第一个不等式有

则式(10)可以写为

另一方面由于PC为firmly非扩张以及引理1,所以有
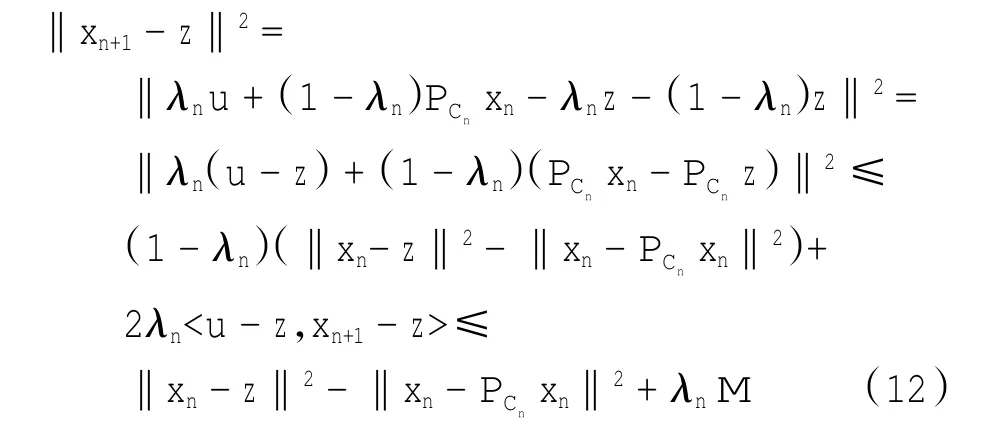
这里M是某一实数,使得2‖u-z‖·‖xn+1-z‖≤M(注意到(xn)是有界的)。
令
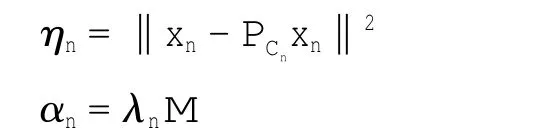
那么式(12)可以写为


[1]YANG Q.On variable-set relaxed projection algorithm for variational inequalities[J].J Math Anal APPL,2005(302):166-79.
[2]YANG Q.The relaxed CQ algorithm for solving the split feasibility problem[J].Inverse Problems,2004,20(4):1261-1266.
[3]XU H K.Iterative methods for the split feasibility problem in infinitedimensional Hilbert spaces[J].InverseProblems,2010,26(10):105018-105034.
[4]ZHAO J,YANG Q.Self-adaptive projection methods for the multiplesets split feasibility problem[J].Inverse Problems,2011,27(3):35009-35021.
[5]LÓPEZ G,MARTÍN-MÁRQUEZ V,WANG F H,et al.Solving the split feasibility problem without prior knowledge of matrix norms[J].Inverse Problems,2012,28(8):85004-85021.
[6]H S,Y C.Solving the variational inequality problem defined on intersection of finite level sets[J].Abstract and Applied Analysis,2013,doi.org/10.1155/2013/942315.
[7]GOEBEL K,KIRK W A.Topics on Metric Fixed Point Theory[M]. Cambridge:Cambridge University Press,1990.
[8]BAUSCHKE H H,BORWEIN J M.On projection algorithms for solving convex feasibility problem[J].SIAM Rev,1996(38):367-426.
(责任编辑:杨媛媛)
Simple algorithm for projection operator
HE Song-nian,ZHAO Zi-yi
(College of Science,CAUC,Tianjin 300300,China)
A relaxed Halpern's projection algorithm is proposed.Since this algorithm computes the projection onto level set of a convex function by computing the projection onto a series of half-spaces containing a level set,it is easy to be implemented.Strong convergence of this algorithm is proved.
projection;half-space;strong convergence;Hilbert space
O177
:A
:1674-5590(2014)04-0052-03
2013-07-12;
:2013-09-02
:中央高校基本科研业务费专项(3122013SY30)
何松年(1963—),男,山西太原人,教授,博士,研究方向为非线性分析理论、算法及其应用.
