一种改进的先验概率粗集模型

陶 志，刘彩平

（中国民航大学理学院，天津 300300）

一种改进的先验概率粗集模型

陶 志，刘彩平

（中国民航大学理学院，天津 300300）

基于容差关系和先验概率容差关系的粗糙集模型是粗糙集理论的重要扩充，但却均有其局限性。本研究结合上述两种模型的优点，提出了一种改进的先验概率粗糙集模型，新模型是建立在对不完备决策系统属性值统计数据的基础上，既考虑了同一属性取值的不同情况，又考虑到不同属性之间的关联性，可以有效提高分类精度和分类的合理性。该模型对属性间存在明显的关联性且未知属性值较少的系统具有很强的实用性。

粗糙集；不完备决策系统；改进的容差关系

粗糙集理论自1982年由波兰学者Z.Pawlak提出以来[1]已被广泛应用于数据挖掘、人工智能、模式识别、机器学习及智能信息处理等领域。但Pawlak所提出的理论是基于信息系统是完备的这样一个假设，而实际问题中由于数据采集手段及数据精度要求不同等原因，使得需处理更多的是不完备信息系统，即系统中的部分属性值是未知的。这就要求对经典的粗糙集理论进行扩充。目前，对不完备信息系统的处理主要有两种方法：一种是间接法，即通过领域专家把所缺失的数据补齐[2]，间接地把不完备信息系统转化为完备系统；第二种是直接法，即直接把粗糙集理论中的相关概念在不完备信息系统中进行扩充[3-7]。间接法因为有领域专家的参与而主观性比较强，而直接法由于其相对比较客观，因此引起学者的广泛关注。

针对不完备信息系统，目前主要提出了容差关系和相似关系两种扩充模型[3-4]，以及对这两种模型的改进形式（如限制容差关系[5]、限制非对称相似关系[6]等）。基于上述两种改进模型，又有学者提出先验限制容差关系粗糙集模型[7]和先验限制非对称相似关系粗糙集模型等基于先验概率的粗集模型。然而，上述基于先验概率的粗糙集模型对已知信息只考虑了单个属性内部的纵向比较，由单个属性上属性值出现的概率来确定该属性中未知属性的取值，却忽略了各属性间的联系，对同一元素的其他已知属性值不进行考查，因而造成了信息的浪费。事实上，许多属性之间并不是相互独立的，而是相互制约、相互推定的，即条件属性之间也有决策关系存在。例如，中国法律规定男性公民到了22周岁才能登记结婚，那么对于一个婚姻情况未知的人，可以根据他的已知属性年龄小于22岁以及他是男性推断出他是未婚的。即使所得到的信息系统中婚姻状况里出现概率最大的是已婚，也不能简单按婚姻状况的先验概率确定这个人的婚姻状况为已婚。这个例子说明，在对先验信息进行处理时还应该横向参考这个元素的其他已知属性值。本文通过对现有先验概率粗集模型的研究，提出一种基于属性间依赖关系的改进先验概率容差关系，并讨论了改进的先验概率容差关系粗糙集模型的特点及其相关性质。新模型对已知信息的利用更加充分，既提高了分类精度又使分类更趋合理，为不完备信息系统的数据处理提供了一种有效的新方法。

1 基本概念

1.1 不完备决策系统

对于四元组S=（U，AT=C∪D，V，f），U是对象的非空有限集合；AT=C∪D是属性的非空有限集合，C称为条件属性集合，D称为决策属性集合，且C∩D= Ø；∀a∈AT，Va表示属性a的值域；V=∪a∈ATVa表示AT的值域；f为U×AT→V的一个映射，f（x，a）= a（x）∈Va是对象x在属性a上的取值。若至少存在一个属性a∈C使a（x）=*，则称S=（U，AT=C∪D，V，f）是一个不完备决策系统。

1.2 容差关系

Kryszkiewicz提出的容差关系认为未知属性值仅仅是被遗漏但又是确实存在的，因此，“*”被解释为一个任何可能的属性值。

定义1 在不完备决策系统S=（U，AT=C∪D，V，f）中，若所有未知属性值均被认为是遗漏形的（用“*”表示），则由属性集A⊆C决定的容差关系为[3]：TA（x，y）⇔∀a∈A，a（x）=a（y）∨a（x）=*∨a（y）=*，x，y∈U。

显然容差关系具有自反性和对称性，但不满足传递性。

定义2 在不完备决策系统S=（U，C∪D）中，对象集合X⊆U关于属性集A⊆C基于容差关系的上近似集下近似集和近似精度分别为

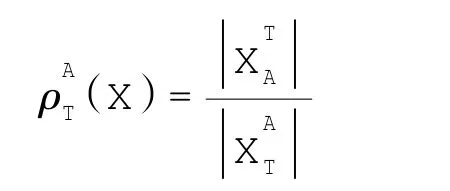
其中

显然

由于容差关系过于宽松，因此会将两个明显不相似的对象判定在同一个容差类中，进而造成不合理分类。为提高同一分类中两个对象间的相似程度，朱颢东等人依据概率统计知识提出了基于先验概率容差关系的粗集模型[7]，从而有效地提高了分类精度。

1.3 先验概率容差关系

在不完备决策系统S=（U，C∪{d}，V，f）中，对于任意一个属性ai∈C，Vi={vi1，vi2，…，vimi}表示ai的值域，Pi={pi1，pi2，…，pimi}表示值域Vi中各个值出现的频率，mi表示该属性值域的大小，那么对象x，y在属性ai∈C上的相似度为

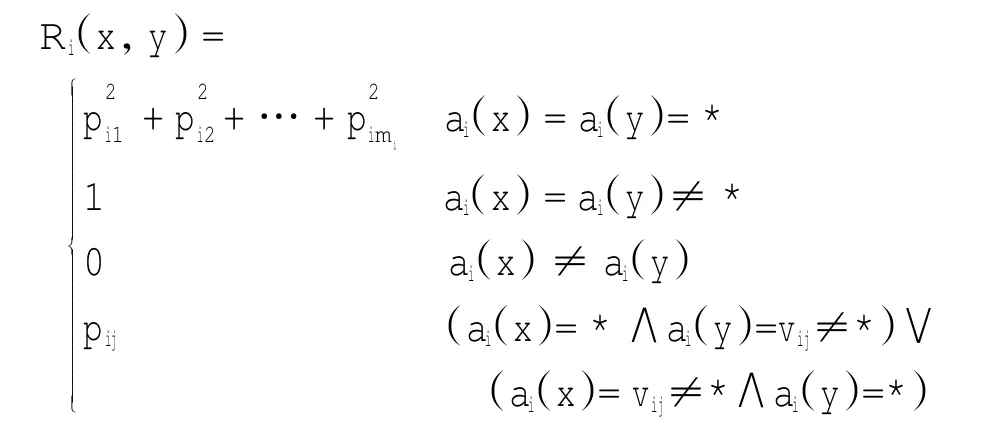
相似度用来度量两个对象间的相似程度，相似度越高说明两对象在某个属性上的相似性越高。

定义3 在不完备决策系统S=（U，AT=C∪D，V，f）中，由属性A⊆AT所决定的先验概率容差关系为：T（A）⇔RA（x，y）≥τ，x，y∈U。其中τ是预先设定好的阈值表示对象x和y在属性集A上的相似度。

如果两个对象在某一属性集上的相似度大于某一阈值，即认为其满足先验概率容差关系，否则就认为不满足。

定义4 在不完备决策系统S=（U，AT=C∪D，V，f）中，对象集合X⊆U关于属性集A⊆C基于先验概率容差关系的上近似集下近似集和近似精度分别为

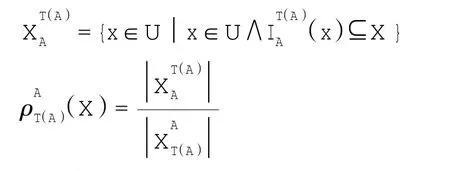
先验概率容差关系在确定未知属性值时，仅从纵向上参考该属性的已知取值，没有考虑属性之间的关联性，因此会造成对未知属性值的片面推断和分类的不合理性。例如，已知有60个人，其中30个欧洲人，20个非洲人，10个亚洲人，且有一个亚洲人的肤色未知，如果按照先验概率容差关系，那么这个亚洲人的肤色被定为白色或者黑色的可能性最大。但是，判断这个人的肤色实际上不应该参考所有人的肤色，而是应该参考已知的9个亚洲人的肤色，这样才更加合理。基于这个思想，提出了改进的先验概率容差关系，新关系全面均衡地考虑了属性间的相互关联及已知和未知属性对相似性的影响，从而使对象间的分类更趋合理，分类精度也得到进一步提高。

2 改进的先验概率容差关系

定义5 在不完备决策系统S=（U，AT=C∪D，V，f）中，由A⊆C所决定的改进先验概率容差关系为

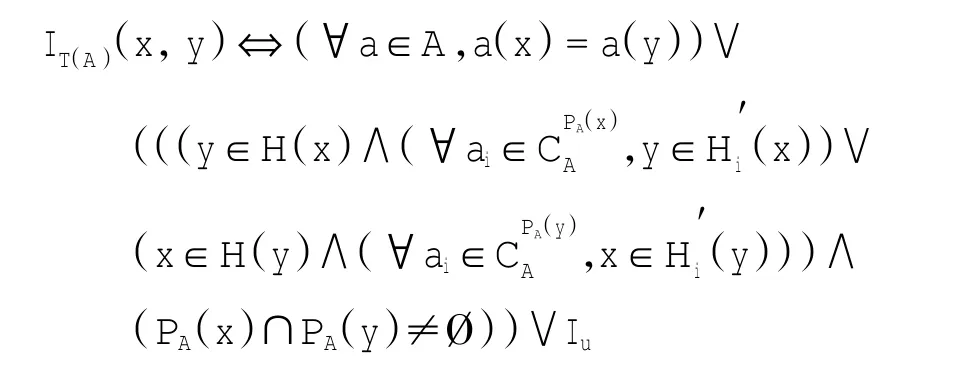
显然，改进的先验概率容差关系是自反的、对称的，但不一定是传递的。

定义6 在不完备决策系统S=（U，AT=C∪D，V，f）中，对象集合X⊆U关于属性集A⊆C基于改进的先验概率容差关系的上近似集下近似集

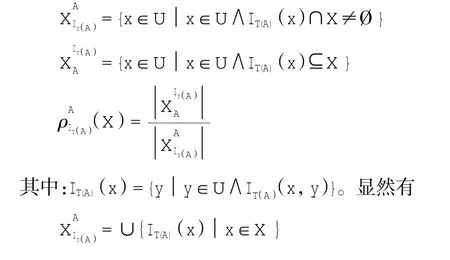
3 改进的先验概率容差关系的性质

定理1 设S=（U，AT=C∪D，V，f）是一个不完备决策系统，由A⊆C决定的改进先验概率容差关系为IT（A），则对于任意X，Y∈U，有：

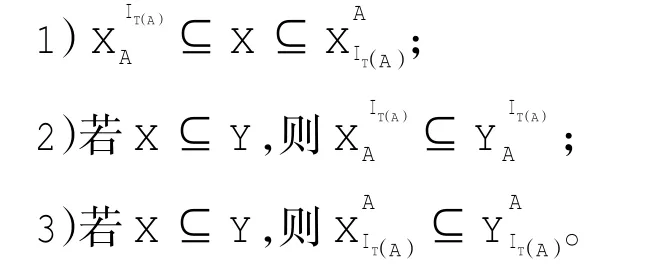
证明由上、下近似定义直接验证即得。

该定理表明，改进先验概率容差关系的上、下近似集合保持原集合的包含关系不变。

定理2 设S=（U，AT=C∪D，V，f）是一个不完备决策系统，A⊆C，X⊆U，对于由A决定的容差关系TA和改进的先验概率容差关系IT（A），下列关系成立：

证明显然，对于∀x，y∈U

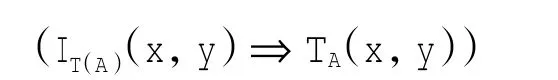
而且

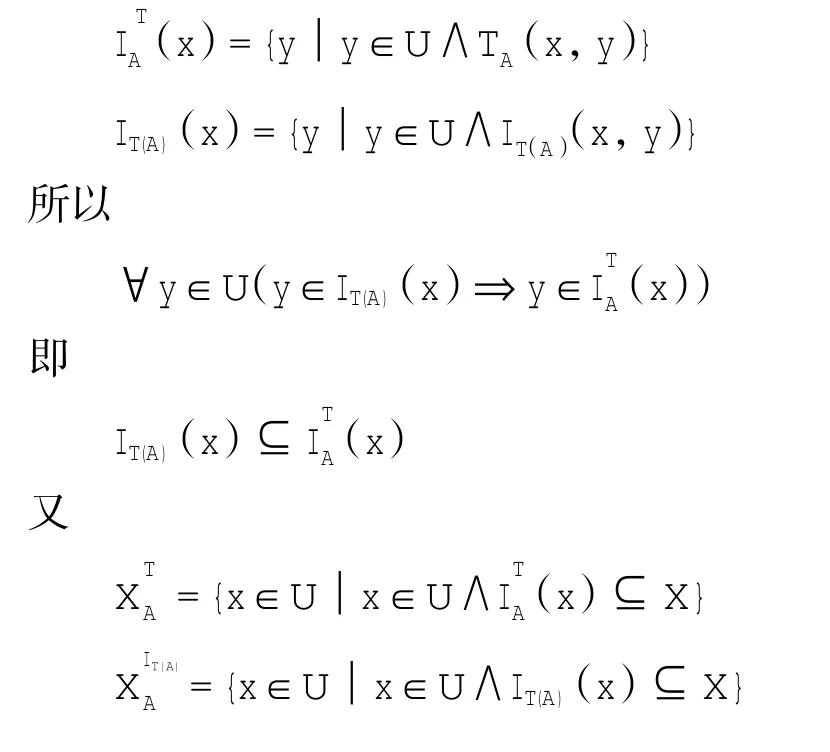
由定理2知，改进的先验概率容差关系与容差关系相比减小了不确定性边界，从而提高了分类精度。

4 实例分析

表1所示为一个不完备决策系统，a1，a2，a3，a4代表条件属性，d是决策属性。U/ind（d）={φ，ψ}，其中：φ={u1，u2，u3，u5，u6，u9，u10}，ψ={u4，u7，u8，u11，u12}。

表1 不完备决策系统Tab.1 Incomplete decision system

现在分别用文中所述的3种粗集模型来处理这个实例。

首先对于容差关系有

近似精度

对于先验概率容差关系，如果取阈值τ=0.3，则有

由于对象u1和u2的后三个属性值均相同，只有u2的第一个属性值未知，按照常理他们不可区分的可能性非常大，但根据先验概率容差关系模型他们却是可区分的，这显然不太符合实际和人在分类中的主观感受（u7和u9及u10和u11也有类似情况）。改进的先验概率容差关系恰好克服了上述不合理性。综上，进一步验证了改进的先验概率容差关系既克服了容差关系分类过于粗糙的缺陷、提高了分类近似精度，又弥补了先验概率容差关系分类的不足。

5 结语

本文分别分析了基于容差关系和先验概率容差关系的粗糙集模型，并针对先验概率容差关系模型在处理未知属性时只参考已知纵向信息而对横向信息运用不足的缺陷，提出一种改进的先验概率容差关系，并在此基础上建立了相应的粗集扩充模型。新模型与容差关系模型相比提高了对象间的相似程度和分类精度，同时又克服了先验概率容差关系模型在分类上的缺陷。通过实例演算，进一步验证了改进的先验概率容差关系的优点。一般在信息系统数据量较大、属性间存在明显关联关系且未知属性值所占比重较小时，用这种模型进行数据处理和分析是可行且具有优势的。下一步应在本文提出的改进先验概率容差关系的基础上，进一步研究不完备系统中属性约简和规则抽取算法，为实际应用系统开发奠定理论基础。

[1]PAWLAK Z.Rough set[J].International Journal of Computer and Information Science，1984，11：341-356.

[2]GRZYMALA-BUSSE J W，FU M.A Comparison of Several ApproachestoMissingAttributeValuesinDataMining[C]//ProcComputing.Berlin：Springer-Verlag，2000：378-385.

[3]KRYSZKIEWICZ M.Rough set approach to incomplete information system[J].Information Sciences，1998，112：39-49.

[4]STEFANOWSKI J，TSOUKIAS A.On the Extension of Rough Sets under Incomplete Information[C]//Proc of the 7th Int’1 Workshop on New Directions in Rough Sets，Data Mining，and Granular-Soft Computing. Berlin：Springer-Verlag，1999：73-81.

[5]王国胤.Rough集理论在不完备信息系统中的扩充[J].计算机研究与发展，2002，39（10）：1238-1243.

[6]瞿彬彬，卢炎生.基于限制非对称相似关系模型的规则获取算法研究[J].小型微型计算机系统，2007，28（7）：1221-1224.

[7]朱颢东，周 姝，钟 勇.不完备信息系统粗集扩展模型[J].湖南科技大学学报（自然科学版），2009，24（3）：73-77.

（责任编辑：杨媛媛）

Rough set model based on improved prior probability

TAO Zhi，LIU Cai-ping
（College of Science，CAUC，Tianjin 300300，China）

Rough set models based on tolerance relation and a prior probability tolerance relation are important expansions of the rough set theory，yet there are some limitations.Combining the advantages of the two models，an improved prior probability rough set model is proposed.The new model is based on the statistics of property values in incomplete decision system，taking into account both the same attribute's different values and the correlation between different attributes.The model can effectively improve classification accuracy and rationality.The model has a strong practicability in system which has fewer unknown attribute values and exists a significant association in different attributes.

rough set；incomplete system；improved tolerance relation

TP18

：A

：1674-5590（2014）08-0048-04

2013-06-17；

：2013-10-14

国家自然科学基金项目（60672178）；中国民航大学科研基金项目（2010kys01）

陶 志（1963—），男，辽宁沈阳人，教授，博士，研究方向为复杂系统建模、粗糙集理论及其应用等.