非全日制工程硕士研究生数学学位课的教学改革与实践

2014-02-24褚宝增王训练张寿庭王祖朝王根厚王翠香

中国地质教育 2014年1期

关键词：工程硕士非全日制研究生

褚宝增，王训练，张寿庭，王祖朝，王根厚，王翠香

1.中国地质大学（北京）数理学院，北京 100083；2.中国地质大学（北京）地球科学与资源学院，北京 100083

课程建设

非全日制工程硕士研究生数学学位课的教学改革与实践

褚宝增1，王训练2，张寿庭2，王祖朝1，王根厚2，王翠香1

1.中国地质大学（北京）数理学院，北京 100083；2.中国地质大学（北京）地球科学与资源学院，北京 100083

由于非全日制工程硕士入学资格考试相对灵活，学生年龄差异明显偏大，导致数学基础参差不齐，给数学学位课的教学带来极大困难。为了保障基本的培养要求，必须对教学方法进行改革，教学内容进行取舍。最终使非全日制工程硕士研究生具备完善的数学逻辑思维能力，能够独立正确选择合理的数学手段应用到自身实际的工作与科研当中，从而明显提升工程硕士研究生的创新意识。

非全日制；工程硕士；数学教学；GCT

任何一项教学改革首先都必须了解清楚教学对象的基础水平。非全日制工程硕士不同于全日制工程硕士。本文从非全日制工程硕士入学考试的方式以及学员的年龄与知识结构的分析入手，提出数学学位课具体的教学内容与教学方法的改革方案，以达到预期的教学目的。

一、入学考试方式

为了适应我国高层次创新型人才培养的要求，有效选拔创新型人才培养的对象，2003年，国务院学位委员会制定并施行了面向在职人群的研究生入学资格考试的两段制考试。第一段称“研究生入学资格考试”（Graduate Candidate Test），简称GCT，由国家教育主管部门委派专门的考试机构统一组织[1-2]。第二段为招生院校自行组织的专业考试。最终根据考生的GCT成绩、专业笔试成绩、面试成绩等决定是否录取[3]。

第一段的GCT试卷由四个部分构成，分别是：语言、数学、逻辑、外语。全部为选择题，满分400分，除第二部分数学25题每题4分外，其他三部分每部分50题每题2分。值得特别重视的是，四部分合成一卷，仅有3个小时的考试时间，每部分若均分只有45分钟，扣除涂卡时间，语文、逻辑、英语每题只有50秒，数学每题只有100秒，别说做完，除数学外的其他三部分读题都读不完。考虑到我国绝大多数院校对第一段的录取分数要求在200分左右，考生对待考试的具体战略就是：各部分只选择做有把握的半数题目，余者不做，统一涂卡，在每一道题上时间加倍，这样取者正确率高，舍者用概率去撞，由此做200分的题目获200分的成绩，便非难事。下面笔者就第二部分数学做具体的战略取舍分析。

二、学员结构分析

非全日制工程硕士生源不一，基础知识参差不齐。有些是参加工作刚满3年的毕业生，像计算机技术与软件工程专业领域的毕业生，均具备较好的理论知识；有些是工作单位的骨干，甚至是主管领导，本科毕业多10年以上，虽有较丰富的实践经验，但基础知识已经十分生疏[4]。

笔者对在京3所重点高校部分非全日制工程硕士研究生的年龄进行随机抽取统计，从2004级

到2012级，连续9年，平均年龄分布见图1。

图1直观地表现出平均年龄成逐年下降趋势，累加下降4岁以上，学生的基础知识遗忘程度减少，确实可以稍微减少教学的困难。再看图2，历年年龄标准差改变不大，说明学员间对基础知识的差异程度没有改观。9年中，学员年龄的极差全部在20岁以上，加之学员基础知识面本身不够宽泛，教学课程内容的设计上很难统一。既基本满足教学大纲的要求，又尽量照顾学生的实际状况，从宏观上适当调整教学内容与局部处具体优化教学环节就显得十分重要。

图1 2004—2012年非全日制工程硕士研究生平均年龄（期望）

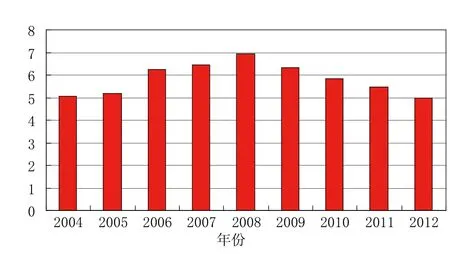
图2 2004—2012年非全日制工程硕士研究生年龄标准差

三、课程的选取与内容的调整

在非全日制（在职）工程硕士的培养计划中，数学学位课称为“应用数学”，最初48学时计3学分，后来调整为40学时计2学分。实际是根据专业的不同需求在《科学和工程计算基础》、《应用概率统计》与《运筹学基础》教材中三选一。

这套工程硕士应用数学系列教材是由国务院学位委员会组织专家编写，清华大学出版社出版发行。在编写时力求做到通俗易懂，深入浅出。对理论问题只作必要的叙述，舍去严格证明，目的是引导学生开阔视野。而着力提供有关的实际背景，理论联系实际，阐明应用理论解决实际问题的方法。书中的例题大多来源于实际，给学生提供了解决实际问题的手段，培养学生依据基本理论懂得构造、评估、选取、甚至改进的方法，有助于提高学生独立分析问题和解决问题的能力[5]。

为了合理利用教材和选择教学内容，下面对上述三本教材的内容作简要的介绍。《科学和工程计算基础》包括：线性代数方程组的数值解法、插值和拟合、数值积分和数值微分、常微分方程的数值解法、非线性方程和方程组的解法、最优化方法、矩阵特征值问题的数值解法等。《应用概率统计》包括：随机事件及其概率、离散型与连续型随机变量、随机变量的数字特征、多维随机变量、极限定理、数理统计的基本概念、参数估计、假设检验、方差分析、回归分析、正交试验设计、可靠性设计等。《运筹学基础》包括：线性规划、单纯形法、线性规划的对偶理论、运输问题、线性规划应用实例、整数规划、目标规划、非线性规划、无约束问题的最优化方法、约束问题的最优化方法、动态规划、决策分析等。

图书馆是少年儿童课外自主学习的重要场所，起到补充学校教育的作用［7］。福安图书馆积极与社会机构合作，实现多样化的阅读资源整合，以丰富多彩的内容吸引读者关注，打造了多种公益文化服务品牌。其中“阳光课堂”就是该馆精心策划，通过多方考察与研讨，寻求社会教育机构、家长、专业人士的建议，共同打造的青少年课外教育机构。自2005年运行以来，“阳光课堂”已经举办超过400期培训活动，内容包括英语、绘画、音乐、科普知识等，形式多样，新颖有趣，深受广大小读者与家长的喜爱。它不仅为未成年人搭建了获取知识的平台，也有助于激发孩子们的学习兴趣和增进亲子关系。

《科学和工程计算基础》应用对象主要是工程实际中常用的数值计算方法，《应用概率统计》应用对象主要是随机现象的统计规律问题，《运筹学基础》应用对象主要是管理科学领域。以中国地质大学（北京）非全日制（在职）工程硕士的“应用数学”课为例，机械工程、建筑与土木工程、电子与通信工程、计算机技术、软件工程、安全工程、水利工程、环境工程、石油与天然气工程专业领域选择《科学和工程计算基础》的主要内容，地质工程、矿业工程、材料工程、化学工程、测绘工程专业领域选择《应用概率统计》的主要内容，工业工程、项目管理专业领域选择《运筹学基础》的主要内容。

如上的选取方法简单明确，但缺点是不能满足专业的系统需求。比如地质工程专业领域，虽然以利用统计学知识为主，然也需要数值积分与插值的知识；再者软件工程专业领域，虽然以掌握数值计算为主，然也需要应用规划与最优化的方法；还有水利工程专业领域，还需要补充微分方程数值解的有限差分方法。这就要求任课教师，在选定大的数学门类后，根据专业领域的具体需求，进行合理的取舍、调整和补充，以达到对专业领域服务的最佳效果。具体授课内容建议见表1。

四、具体教学内容的改革

笔者主张，对教学内容首先要“化繁为简”，对解决同一个问题的诸多方法，选择出最实用有效的方法，在此基础之上，还需“将简剖细”，讲解论证此方法的预备知识、产生此方法的动因契机、推导此方法的缜密过程、应用此方法的注意事项。看似精简了教学内容，实际可以通畅课程的全部脉络，从而保障了健全的课程体系。

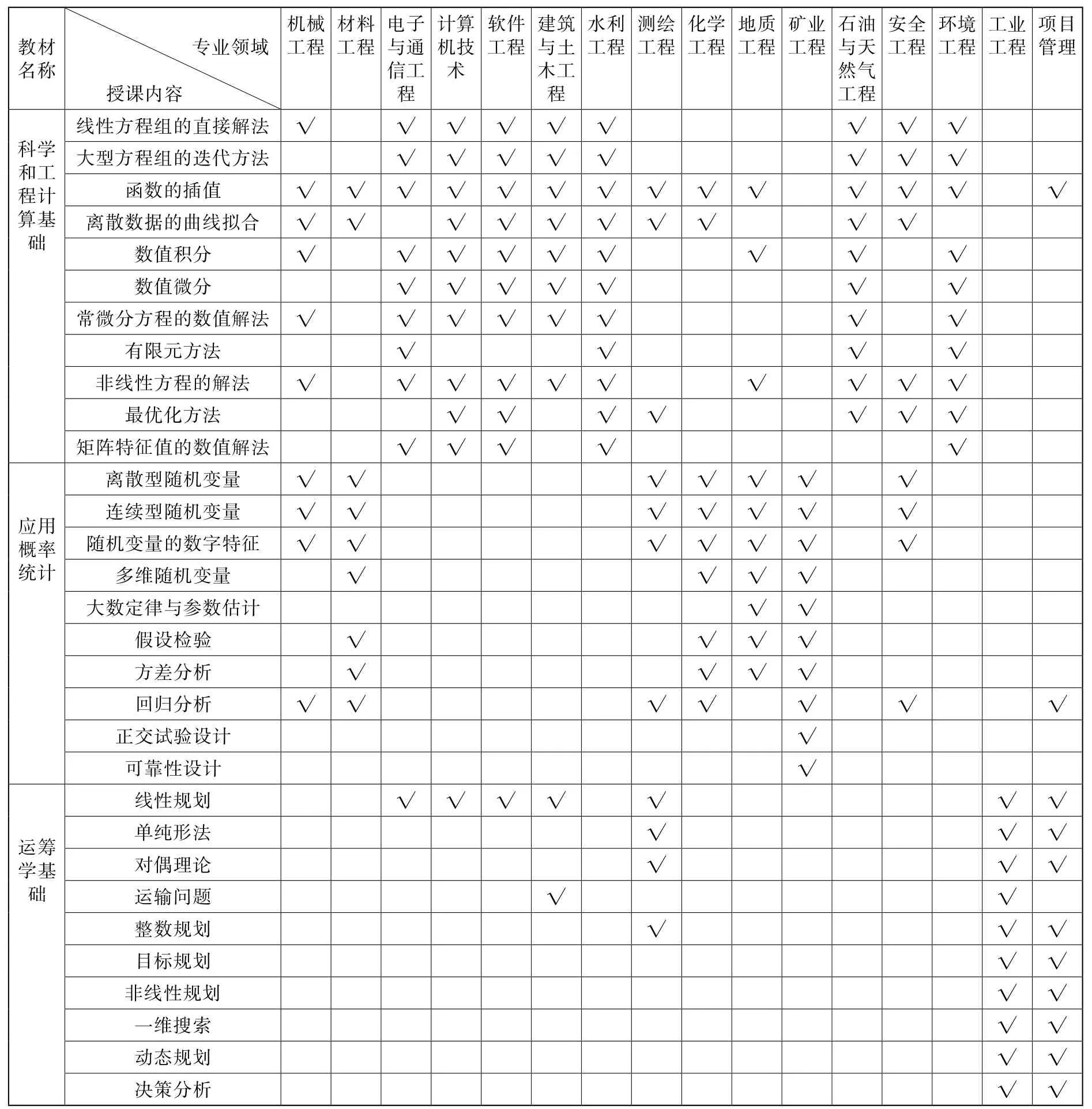
表1 中国地质大学（北京）非全日制工程硕士授课内容选择表

在选定教学内容的门类及其范围后，就需要进一步对具体教学环节的教学方法进行研究。40学时对在校全日制硕士研究生而言确实不少，然而对基础知识多年荒废后又没有足够时间事先重温的非全日制工程硕士研究生而言就显得十分紧张。下面就一些具体之处的教学处理做简要介绍，以体现教学改革的思想。

在“科学和工程计算基础”课“数值积分”一节余项的推导中，梯形积分公式的余项可以利用第一积分中值定理对插值公式的余项积分推出，而辛卜生积分公式的余项按常理也应对其插值公式的余项进行积分，然二阶插值公式的余项已经不再满足第一积分中值定理的条件。多数《数值分析》的教材都是先引出一个证明过程复杂的积分余项定理，即等距节点插值型求积公式的余项定理。

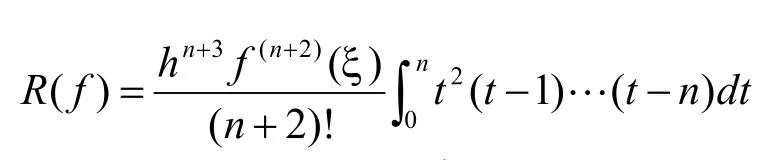
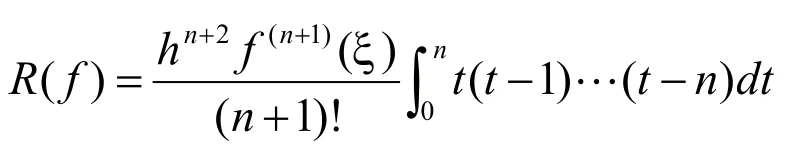
上边定理若证明，则学员不易理解，若不证明，则学员难以接受。如选择用代数精确度的理论进行推导，便可使学员易于理解与接受。

还有在“科学和工程计算基础”课“多项式拟合”一节，多数数值分析的教材将其放在“函数逼近”一章，由函数所张成的子空间引出，鉴于学生的基础，如选择用最小二乘法的思想加以介绍，只涉及到多元函数微分的基本理论，避免上升到对非全日制工程硕士研究生而言较为艰深的逼近理论。

并不是所有的公式都有实际应用的价值，利用某些公式可能会产生荒谬的结果，如“科学和工程计算基础”中高阶插值的龙格现象，在多节点又不想删除数据的情况下，建议选择三次样条插值处理。所以学会选择正确的手段和公式十分重要。

在“应用概率统计”课中，其主要内容是回归分析、判别分析、聚类分析、主成分分析与因子分析，由于需要先介绍“概率论”的基础知识，使得课时紧张，故此需要事先了解研究生所学专业，在多种分析中选出其专业主要用的一两种分析进行系统讲解，虽为权宜之计，但并不违背对非全日制工程硕士研究生培养的要求。

在“运筹学基础”课中，要针对实际问题，对现实系统进行详细分析，找出影响系统的主要因素，明确主要目标、主要约束条件、主要参数和变化范围，弄清它们之间的关系，建立描述问题的模型，掌握基本的运筹学模型的典型求解方法，在模型非常复杂或者求解空间的时间复杂度太大时，分析对问题进行进一步的简化的原则，提高学生运用定量分析的方法能够解决实际问题的能力[6]。

通过对“科学和工程计算基础”、“应用概率统计”与“运筹学基础”三门课的分析，提取对非全日制工程硕士研究生所需的知识节点，去掉对非全日制工程硕士研究生无关的知识节点，将所需的知识节点间用理论连接，确保课程体系的完整性。在授课过程中，时常回顾大学数学中“高等数学”、“线性代数”、“概率统计”相关知识点，使学生真正用理解的方式接受新的教学内容。