“平均数”教学片段赏析

钟淑燕

片段一：

师：老师给同学们带来了一些小球，你最想要哪一瓶？（展示数量不一样的小球）

生齐答：第一瓶！

师：为什么呢？

生1：因为第一瓶的小球多。

师：如果要让得到4瓶小球的同学都高兴，怎样办？

生2：4瓶的小球要一样多。

生3：将小球平均分。

生4：把瓶子里的小球加起来，求出平均数再分。（多数同学同意这种做法）

师：这位同学说得很好，他想到的这种方法，老师给它取一个名字，叫作“求和均分”。

生1：我还可以把多的小球拿出来，分给少的，使4瓶的小球一样多。

师：真是爱动脑的孩子，他的这种做法，老师也给它取了一个名字，叫作“移多补少”。

赏析：关注学生生活，以“公平分球”激发学生学习兴趣，并利用学生已有的知识经验寻求解决问题的方法。在探究求平均数的方法时，给学生充分的展示平台，当学生说到“把瓶子里的小球加起来，求平均数”时，教师用“求和均分”概括了这种求平均数的方法；当学生提到“把多的小球拿出来，分给少的，使4瓶的小球一样多”时，教师用“移多补少”总结了求平均数的另一种方法。在学生生活经验积累的基础上总结出求平均数的方法，不仅体现数学来源于生活的理念，而且真正体现学生是学习的主人。另外，从课堂导入环节来看，这样的导入方式“简而不繁”，直奔重点。

片段二

出示两个求平均数的式子：（8+6+5+9）÷4=7（个），（2+3+7+16）÷4=7（个）。

师：观察两道式子的平均数与各数量，你发现了什么？

生1：第一个式子里的括号中有两个数比平均数大，还有两个数比平均数小。

师：你的眼睛真亮，还有不同发现吗？

生2：第二个式子的括号里还有一个数与平均数相等。

生3：两组数据的数有的比平均数大，有的比平均数小，还有的与平均数相等。

师：这位同学观察得很全面，还有哪位同学的发现与他一样？

生4：我发现平均数可能比一组数据中的某个数大，可能比某个数小，也可能与某个数相等。

赏析：学生对理解平均数的意义可能会很模糊，教师在设计时通过观察平均数与数据中的数，让学生发现平均数是介于大数和小数中间，这样一来，学生对理解平均数的特点和意义就容易多了。其次，通过“观察——发现”这一探究过程，可以培养学生的数感，为用平均数解决生活中的问题做好铺垫。

版段三

师：同学们真棒，老师奖励最认真听课的同学玩拍球游戏。（要求：把12位同学分成两个小组，限时10秒，比哪个组拍的次数最多）

师：老师想知道两个组的同学拍球次数的排名，怎么算？

生1：算出每个组拍球次数的平均数，再比较平均数，平均数大的排第一。

师：你真棒，还有不同算法吗？

生2：我觉得只要求出每组拍球总的次数就可以了，因为两个组的人数一样多，总数大的平均数就大。（多数同学赞同这种算法）

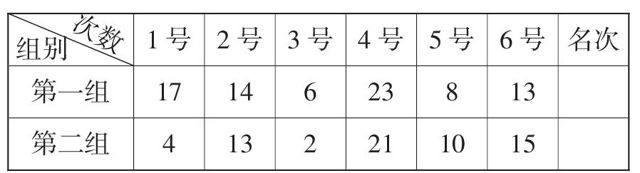
师：你真了不起，老师的算法也和你一样。老师把第三次拍球的机会奖给你们组。（让4位同学再次拍球）展示三个组拍球情况

师：从表中可以看出，第一组的成绩最好。

生：不公平！（众多同学抗议）

师：怎么不公平呢？

生：第一组与第二组有6个人拍球，而第三组只有4个人拍球，不能用总数排名，只能用平均数排名才公平。

赏析：成功的数学课不在于用了多少学具，而是要合理地利用所准备的学具。以4瓶小球探究出求平均数的方法，充分利用学生玩乒乓球的喜好，奖励学生拍球比赛，当教师故意说“第一组成绩最好”时，引起同学们的“抗议”，此时老师并没有马上对同学们的“抗议”作出解释，而是问“怎么不公平”？将疑问还给学生，让学生在讨论问题中理解为什么要求平均数。这样的设计给学生营造了一个轻松的学习环境，让学生在讨论中领悟新知识。

片段四：

教师出示练习：小河的平均水深110厘米，小红身高112厘米。小红虽不会游泳，但在河里玩耍不会有危险。你同意这种说法吗？为什么？

生1：我不同意这种说法，因为老师教育过我们不能下河玩耍，这样会很危险。

师：你真是个听话的孩子，能谨记老师的教诲。还有不同想法吗？

生2：我认为小红下河玩耍危险，水的平均深度是110厘米，小红身高112厘米，眼睛到头顶的高度不止2厘米，如果小红下河玩耍，水已淹过了鼻子，会因为呼吸困难而有生命危险。

师：这位同学想得真周到，还有其他想法吗？

生3：我也认为小红下河玩耍会很危险，水的平均深度是110厘米，可有的地方的水会比110厘米深，有的地方的水可能等于或小于110厘米，如果小红到水深的地方玩耍，会很危险的。

赏析：这节课从导入到练习，学生都学得很轻松，掌握得很扎实。整节课将学生从学习观摩者的角色转变成实践者、活动的承载者、过程的生成者的理念在每个片段中体现得淋漓尽致。练习设计量小却紧扣学生生活，不仅加深了学生对平均数的理解，还让学生领悟了怎样用平均数去解决身边的数学问题。

责任编辑：徐新亮