离散耦合非线性Schrödinger格驻波解的存在性

赵 昕

(吉林农业大学 信息技术学院,长春 130118)

在凝聚态物理中,非线性Schrödinger格用于描述晶格的演变.考虑如下耦合离散Schrödinger系统:

(1)

其中:ε>0;k∈;是有界位势(i=1,2,3);A 是离散Laplace算子,(Au)k=uk+1+uk-1-2uk.

通过尺度变换和一些简单的假设,晶格系统(1)可视为时变非线性Gross-Pitaevskii系统中二元物系统的空间离散化形式:

(2)

其中:u(x,t)和v(x,t)为凝聚物波函数;ћ为普朗克常数除以2π;m为原子质量;Vi为第i个超精细状态的势阱;ai≥0表示相关的轴频率(i=1,2,3,4).系统(2)应用于由两种不同的超精细“玻色-爱因斯坦”凝聚态[1]组成的二元混合物中,目前关于系统(2)的驻波研究已有很多结果[2-6],关于离散非线性系统的局部化驻波解的存在性研究也取得了一定的进展.如Aubry等[7-9]通过驻波的存在提出了反延续或反可积性的概念,深入探讨了离散非线性Schrödinger方程.研究该结构的数学技巧有动力系统技巧、变分方法和拓扑技术等,如同伦方法[10]、山路引理[11]、Nehari流形[12]和Krasnoselskii不动点定理[3].本文用Nehari流形方法研究晶格系统(1)驻波解的存在性.

设

uk(t)=exp(-iω1t)φk,vk(t)=exp(-iω2t)ψk,k∈,

(3)

将式(3)代入式(1),可得如下等价方程组:

(4)

考虑

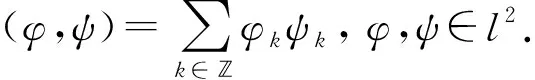
(-Aφk,ψk)=(B*Bφk,ψk)=(Bφk,Bψk),

进而有

即A:l2→l2为有界算子且σ(-A)⊂[0,4].定义在l2中的自伴算子:

K1=-εA+V1-2V2, K2=-εA+V3-2V2.

(5)

(H2) 频率ω1和ω2满足

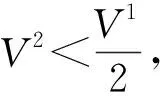
仿照文献[8-9,12]的结果,可得下列3个引理.

引理1假设条件(H1)成立,令

则对于任意的p(2≤p≤∞),S1和S2紧嵌入到lp中,并且谱σ(K1)和σ(K2)分别是离散的.

定义能量函数

(6)

和Nehari流形

N∶={(φ,ψ)∈l2×l2: H1(φ,ψ)=H2(φ,ψ)},

(7)

其中:

注1由引理1可知,能量函数E(φ,ψ)∈1(l2×l2,).

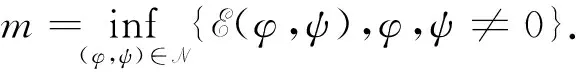
(8)

从而定理1的证明可归结为如下两个命题.

命题1序列{φn}和{ψn}分别在Hilbert空间S1和S2内有界,并且存在φ*∈S1和ψ*∈S2,使得φn→φ*,ψn→ψ*∈l2.

命题2(φ*,ψ*)∈N且E(φ*,ψ*)=m,则 (φ*,ψ*)是代数系统(4)的一个非平凡弱解.

由引理1～引理3,再利用Nehari流形技巧,即可证明命题1和命题2,从而定理1成立.

[1] Pitaevskii L P,Stringari S.Bose-Einstein Condensation [M].Oxford: Clarendon Press,2003.

[2] Amborosetti A,Colorado E.Standing Waves of Some Coupled nonlinear Schrödinger Equations [J].J Lond Math Soc,2007,75(1): 67-82.

[3] Belmonte-Beitia J,Pére-Garacía V M,Torres P J.Solitary Waves for Linearly Coupled Nonlinear Schrödinger Equations with Inhomogeneous Coefficients [J].J Nonlinear Science,2009,19(4): 437-451.

[4] Hioe F T.Solitary Waves forNCoupled Nonlinear Schrödinger Equations [J].Physical Review Letters,1999,82(6): 1152-1155.

[5] Kanna T,Lakshmanan M.Exact Soliton Solutions,Shape Changing Collisions,and Partially Coherent Solitons in Coupled Nonlinear Schrödinger Equations [J].Physical Review Letters,2001,86(22): 5043-5046.

[6] Aubry S.Breathers in Nonlinear Lattices: Existence,Linear Stability and Quantization [J].Physica D: Nonlinear Phenomena,1997,103(1/2/3/4): 201-250.

[7] Aubry S.The Concept of Anti-integrability Applied to Dynamical Systems and to Structural and Electronic Models in Condensed Matter Physics [J].Physica D: Nonlinear Phenomena,1994,71(1/2): 196-221.

[8] Johansson M,Aubry S.Existence and Stability of Quasiperiodic Breathers in the Discrete Nonlinear Schrödinger Equation [J].Nonlinearity,1997,10(5): 1151-1188.

[9] Mackay R S,Aubry S.Proof of Existence of Breathers for Time-Reversible or Hamiltonian Networks of Weakly Coupled Oscillators [J].Nonlinearity,1994,7(6): 1623-1670.

[10] Rothos V M,Bountis T C.The Dynamics of Coupled Perturbed Discretized NLS Equations [J].Physica D: Nonlinear Phenomena,1998,113(2/3/4): 326-330.

[11] Karachalions N I,Yannacopoulos A N.Global Existence and Compact Attractors for the Discrete Nonlinear Schrödinger Equation [J].J Differential Equations,2005,217(1): 88-123.

[12] Pankov A,Rothos V.Periodic and Decaying Solutions in Discrete Nonlinear Schrödinger with Saturable Nonlinearity [J].Proceedings of the Royal Society A: Mathematical,Physical and Engineering Sciences,2008,464(2100): 3219-3236.