三角形网格规则点的多进制细分算法

赵义武,娄 岩,李 强,战 扬,梁学章

(1.长春理工大学 空间光电技术国家地方联合工程研究中心,长春 130022;2.吉林大学 数学学院,长春 130012)

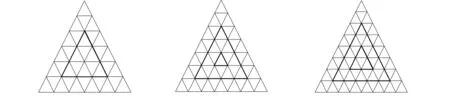
对基于三角形网格的多进制曲面细分算法的研究目前已有许多结果.文献[1-7]讨论了基于三角形网格的三进制细分算法;文献[8-9]讨论了二元Box样条和最小支集二元B样条的多进制细分方法;文献[10]给出了Ⅰ型和Ⅱ型剖分上的多元B样条多进制细分方程;文献[11]给出了多进制细分在规则点的掩模表达式,但未给出严格证明.图1为初始网格与应用三进制Loop细分算法2次的结果及在规则点的三进制细分掩模.

上述方法均未给出规则点的多进制细分掩模的显式表达式,也未严格说明掩模用到点的范围.事实上,二进制细分算法存在局限性,如当初始网格确定后,对每次细分生成的点不能进行人为控制,经常会遇到前一步细分生成的点数不满足实际需求,而再细分一次生成的点有大量冗余的情况.不仅需要大量的内存和硬盘空间,增加了计算量,提高了对运算和显示设备的性能要求,而且在后期的渲染和显示时,经常出现“慢”和“卡”的现象.解决这些问题的方法是改变细分算法的进制,根据实际需求确定细分进制,从而克服二进制细分算法的局限性,并能满足实际需求.

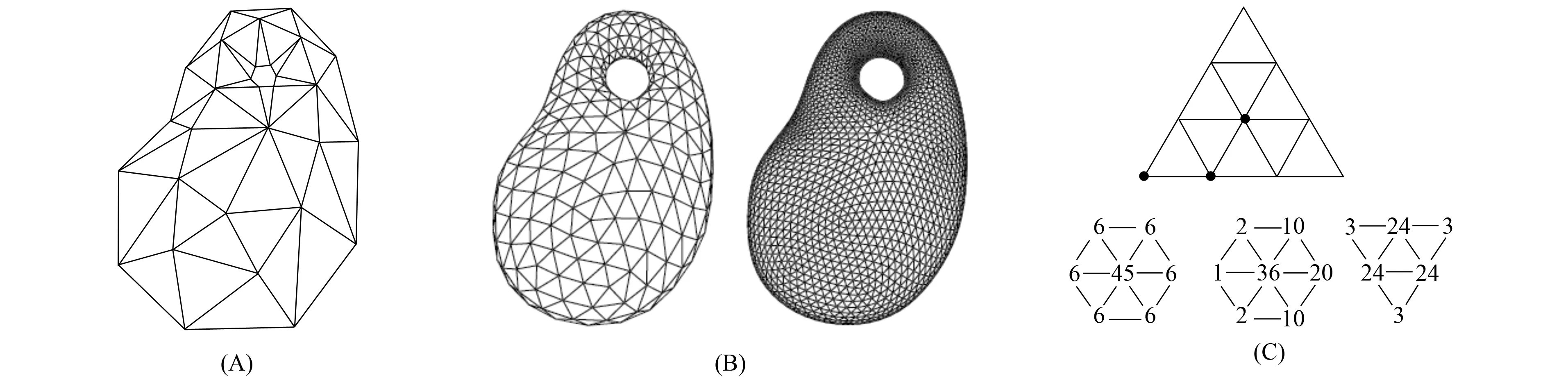
图1 初始网格(A)与利用三进制Loop细分算法2次的结果(B)及规则点的三进制掩模(C)Fig.1 Original control mesh (A) followed by two ternary Loop subdivisions (B) and regular masks (C)

1 预备知识

掩模(Mask)也称为面具,表示在细分过程中利用旧点生成新点的计算规则.掩模的系数表示相应的旧点对生成新点的贡献.若一个点有n条边与它相连,则称该点的价为n.对三角形网格,规则点的价为6(规则边界点的价为4).

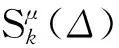
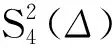
(1)

其中

(2)

l1和l2的奇偶性相同，且

(3)

1.1 M进制细分时需要给出掩模公式的点数

在细分过程中,虽然需要计算的新顶点、新边点和新面点的个数很多,但根据对称性,许多新点采用的掩模系数结构相同,从而极大减少了需要给出掩模公式的点个数.在一个三角形内,需要给出掩模公式的点数如下.

1) 顶点数：需要给出掩模的顶点数为1.

3) 面点数：采用从三角形三边形成的环向内收缩的方法来考虑需要给出掩模的面点个数,最终收缩的结果必为下列3种情况之一：

① 收缩结果为1个点,最后一层环上需要给出掩模的面点数为1,如图2(A)所示;

② 收缩结果为1个小三角形,最后一层环上需要给出掩模的面点数为1,如图2(B)所示;

③ 收缩结果为1个大三角形,最后一层环上需要给出掩模的面点数为2,如图2(C)所示.

(A) 收缩结果为1个点 (B) 收缩结果为1个小三角形 (C) 收缩结果为1个大三角形图2 收缩结果Fig.2 Contraction results

命题1当M=6k+i(i=0,1,…,5)时,需要给出掩模公式的面点数为

fnum=3k2+ik+t,

其中: 当i=0,1,2时,t=0；当i=3,4时,t=1;当i=5时,t=2.

1.2 系数的计算公式

(4)

2 M进制细分掩模的计算

2.1 计算方法

引理1给出的细分公式是Fourier变换形式,不是显式计算公式.下面推导掩模的显式计算公式.先确定哪些旧顶点对新点有贡献,然后求出相应的掩模系数.不失一般性,新生成的点应包括新顶点、多个新边点及多个新面点,本文仅讨论M≥4的情形.M=2,3时的情形类似.

根据引理1，有

利用Fourier逆变换,可得

其中l1和l2及l3和l4分别满足式(3).

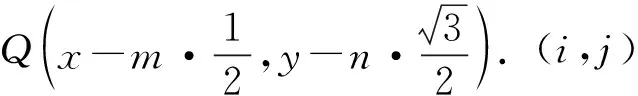
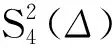
注意到s(x,y)在加密网格上的表示为

而Q(x,y)在加密网格上可表示为

(5)

从而

设s(x,y)=Q(x,y).当M=2时,在Q(x,y)支集中对生成的部分点标号如图3所示.

另一方面,由

显然Mm=l1+l3≤4M-4,可得

且Mn=l2+l4≤2M-2,从而

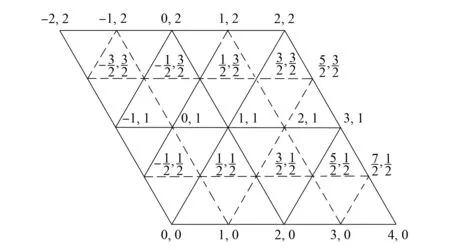
图3 M=2时新生成的部分点标号 (虚线为加密的网格)Fig.3 Notation of the generated vertices for M=2 (dotted lines are the refined mesh)

其中m,n∈/M且M·m与M·n同奇偶.又由|l1|+|l2|≤2M-2且|l3|+|l4|≤2M-2,得从而对所有的cm-i,n-j,仅当且时,cm-i,n-j≠0.这里l1～l4共有(3M2-3M+1)2种情况,利用式(4)分别计算每种情况的系数

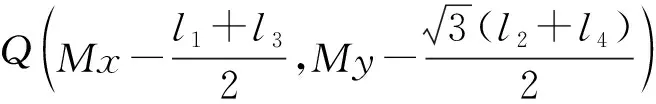
下面以旧顶点(0,0)右上三角形中的点为例给出掩模计算方法.

(6)

2) 新边点的掩模.

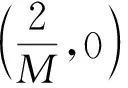
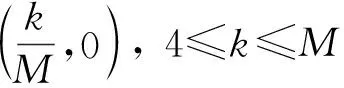
3) 新面点的掩模.

综上,可得:

定理1在M进制三角形细分算法中,在一个三角形上生成的所有新点为围绕该三角形的一层三角形环所有顶点的线性组合,组合公式为式(6)～(11).

图4给出了一个三角形(粗线表示)及围绕此三角形的一层环.

2.2 掩模实例

为了更直观地说明上述方法,下面以M=2的情形为例使用上述方法推导细分算法的掩模公式.此时

其中l1和l2及l3和l4分别满足式(3).这里l1～l4共有49种情况,分别计算系数,合并同类项,再与式(5)比较知,当M=2时,计算得到如图5所示的掩模系数如下: 新顶点：10,1,1,1,1,1,1;新边点：6,6,2,2 (分母统一为24).该结果与Loop给出的二进制三角形细分掩模相同.

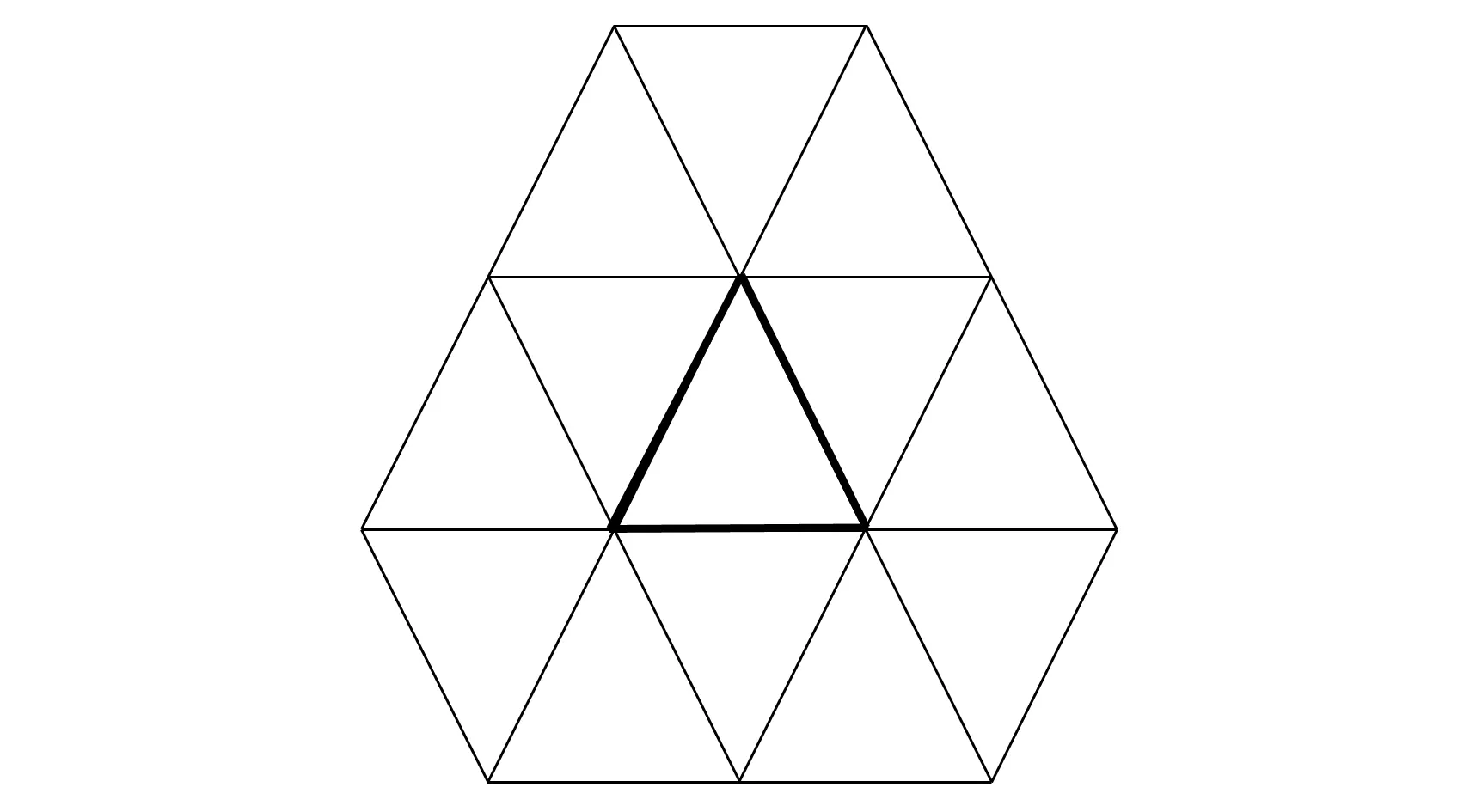
图4 三角形(粗线表示)及围绕此三角形的一层环Fig.4 A triangle (thick line) and the first ring around it

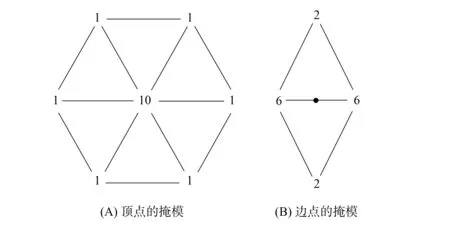
图5 M=2时的掩模Fig.5 Masks for M=2

采用本文方法得到的三进制细分掩模公式与Loop给出的三进制细分掩模公式相同(见图1).对任意给定的M,都可以采用本文方法求得规则点的细分掩模.当M=6时,计算得到如图6所示的细分掩模(分母统一为64)如下:

新顶点：666,105,105,105,105,105,105;

新边点1：630,196,140,140,70,70,50;

新边点2：545,310,165,165,40,40,20,5,5,1;

新边点3：432,432,174,174,18,18,18,18,6,6;

新面点1：570,240,240,90,90,30,30,6;

新面点2：472,356,264,102,50,22,14,10,4,2;

新面点3：372,372,372,54,54,54,3,3,3,3,3,3.

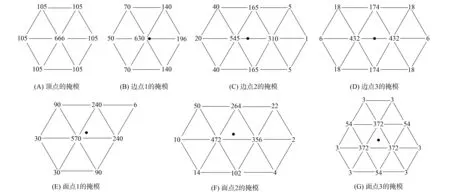
图6 M=6时的掩模Fig.6 Masks for M=6

3 应用实例

图7和图8为利用本文算法得到的五进制细分掩模计算实例.

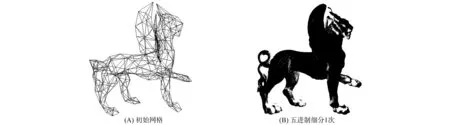
图7 五进制细分实例1(Feline,初始网格有250个点,504个面；五进制细分1次得到258 046个点,516 096个面)Fig.7 Segmentation example 1 by quinary subdivision (Feline,initial mesh with 250 points,504 surfaces,segment 1 get 258 046 points,516 096 surfaces)

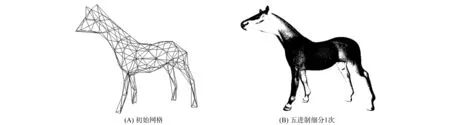
图8 五进制细分实例2(Horse,初始网格有112个点,220个面；五进制细分1次得到112 642个点,225 280个面)Fig.8 Segmentation example 2 by quinary subdivision (Horse,initial mesh with 112 points,220 surfaces,segment 1 get 112 642 points,225 280 surfaces)

综上,本文得到了三角形网格规则点的多进制细分掩模计算方法.此外,利用生成函数的方法也可以得到三角形网格规则点的多进制细分掩模计算方法.结果表明,两种方法所得结果相符.

[1] Loop C.Smooth Ternary Subdivision of Triangle Meshes [C]//Curve and Surface Fitting：Saint-Malo 2002.Brentwood: Nashboro Press,2003：295-302.

[2] Dodgson N A,Augsdorfer U H,Cashman T J,et al.Deriving Box-Spline Subdivision Schemes [C]//Proceedings of the 13th IMA International Conference on Mathematics of Surfaces XⅢ.Berlin: Springer-Verlag,2009：106-123.

[3] Beccari C,Casciola G,Romani L.Shape Controlled Interpolatory Ternary Subdivision [J].Applied Mathematics and Computation,2009,215(3)：916-927.

[4] HAN Bin,JIA Rong-qing.OptimalC2Two-Dimensional Interpolatory Ternary Subdivision Schemes with Two-Ring Stencils [J].Math Comp,2006,75：1287-1308.

[5] LI Gui-qing,MA Wei-yin.Interpolatory Ternary Subdivision Surfaces [J].Computer Aided Geometric Design,2006,23(1)：45-77.

[6] ZHENG Hong-chan,PENG Guo-hua,YE Zheng-lin,et al.A New Ternary Interpolatory Subdivision Scheme for Polyhedral Meshes with Arbitrary Topology [J].Journal of Physics：Conference Series,2008,96(1)：1-7.

[7] Ghulam M,DENG Jian-song.Estimating Error Bounds for Ternary Subdivision Curves/Surfaces [J].Journal of Computational Mathematics,2007,25(4)：473-484.

[8] HAN Li-wen.On the Refinability of Multivariate B-Splines [D].Changchun：Jilin University,2002.(韩力文.关于多元B样条的可加细性质 [D].长春：吉林大学,2002.)

[9] HAN Li-wen,WU Tie-ru.Multiresolution Subdivision of Bivariate B-Splines Based on Integral Method [J].Journal of Jilin University: Science Edition,2002,40(4)：358-360.(韩力文,伍铁如.基于积分方法的二元B样条多尺度细分 [J].吉林大学学报: 理学版,2002,40(4)：358-360.)

[10] GUAN Yu-jing,HAN Li-wen,ZHOU Yun-shi.M-Band Subdivision of Multivariate B-Spline [J].Journal of Computational and Applied Mathematics,2004,163(1)：117-126.

[11] ZHAN Yang.Study of the Masks of M-Band Subdivision Algorithm Based on Triangulation Mesh [D].Changchun：Jilin University,2010.(战扬.基于三角网格的任意尺度细分方法模板研究 [D].长春：吉林大学,2010.)

[12] Chui C K,WANG Ren-hong.Multivariate Spline Space [J].J Math Anal Appl,1983,94：197-221.

[13] ZHAO Yi-wu.On the Refinability of Multivariate B-Splines of Uniform Partition in Three Directions [D].Changchun：Jilin University,2003.(赵义武.均匀三向剖分上的B样条的可加细性质研究 [D].长春：吉林大学,2003.)

[14] ZHAO Yi-wu,HAN Li-wen.M-band Subdivision of Bivariate B-Splines of Uniform Partition in Three Directions [C]//Proceedings on Geometric Modeling and Processing.Los Alamitos,California: IEEE Computer Society,2004：355-358.