基于Mathematica的驻波及弦上驻波的可视化
2022-03-23汪梦雅
曹 蓉, 汪梦雅, 吴 琪
(西藏大学 理学院, 拉萨 850000)
“电磁场和电磁波”是高等院校电子信息与电气工程类专业的一门重要理论课程,其教学内容中包含很多难以理解的概念,并且在学习过程中往往需要求解复杂的微积分方程,因此学生需要花费大量的时间手动推算计算结果,这就增加了学生的学习难度。通过形象化的图形可以帮助学生更好的理解课程中抽象的电磁场和电磁波的概念,编写简单的程序也能够快速得到结果,所以实现电磁场和电磁波的可视化在教学过程中显得尤为重要。
Mathematica是一款功能强大的计算和作图软件。相较于其他数学软件,它有着易上手,好操作等特点,在教学过程中,能够将抽象的概念具体化,复杂的计算简单化,并且在高等院校的很多课程中被广泛应用,本文基于Mathematica软件,实现了驻波概念和结果的可视化,有助于提高学生对“电磁场和电磁波”课程的学习兴趣。
驻波是波的干涉的一种特殊现象,很多教材给出了驻波的一些基本概念,然而对于驻波的实际应用并没有给出详细的描述。本文详细归纳了驻波及弦上驻波的相关内容,并利用Mathematica软件形象地演示了驻波的传播特性,有助于学生更加透彻而深入理解电学中驻波的一系列物理意义。
1 驻波的概念
驻波是波干涉的一种特例,通过波的干涉概念我们可以进一步理解驻波的概念。当两列振动方向相同(纵波或横波)、频率相同且相位差恒定的波在空间同时传播且相遇时,就会表现为空间各点合振动振幅强弱相同的现象,这就是波的干涉,而振幅相同、传播方向相反的两列相干波叠加产生的合成波就形成驻波。
我们知道,在普通物理教材中,通常只研究理想状态下相干波所形成的驻波,但在实际应用中,弦线上驻波的形成往往存在着能量的损失,因此在理想条件下推导出的驻波表达式,在很多时候并不能满足所能达到的结果。然而教材对于驻波的实际应用没有给出比较系统全面的分析和推导,因此本文的重点就是分析驻波传播中能量的损失,从而给出弦线上驻波的一般表达式。
1.1 驻波方程[1]
驻波是由两列振幅相同、传播方向相反的相干简谐波干涉形成的。
设正向波方程和反向波方程为(初相位为0):
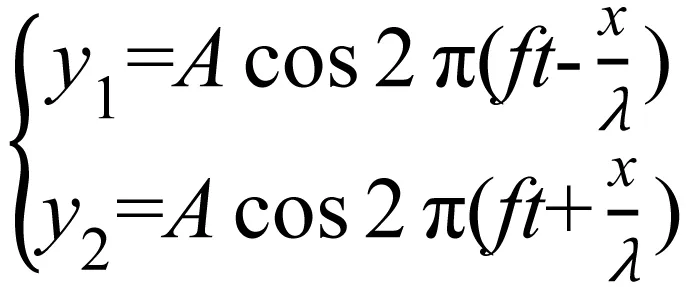
(1)
则两列波在波线上叠加后的合振动为:
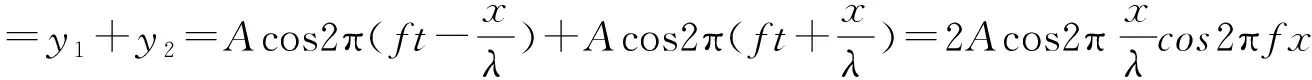
(2)
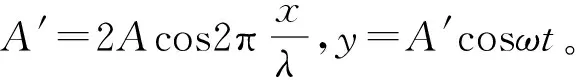
上式(2)表示各点都在作简谐运动,各点振动的频率相同,是原来波的频率。但各点振幅随位置的不同而不同,表明驻波一个重要的特点是介质中各质点都在作稳定的振动,而不是振动的传播。
若坐标原点处相位不为零,则有如下方程:
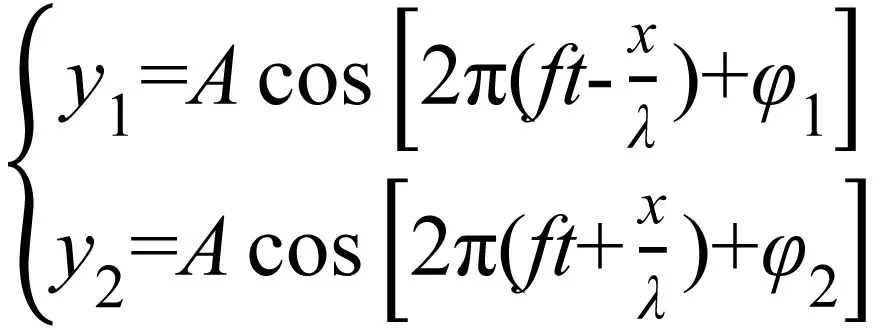
(3)
(4)
其中φ表示相位。
1.2 驻波特征[2]
1) 波腹和波节
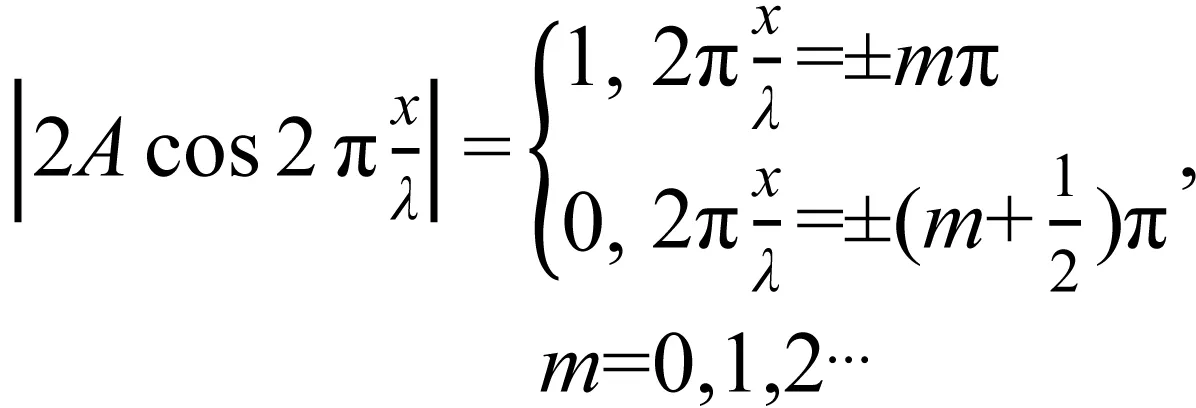
(5)
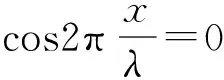
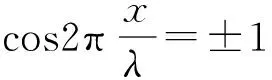
2) 相位分布
(6)
(7)
(8)
上式(6)(7)(8)表明对于所有的质点来说时间部分提供的相位是相同的,而空间变化带来的相位是不同的。并且在波节两侧质点的振动相位是相反的,相邻波节之间质点的振动相位是相同的。
1.3 驻波的能量密度
(9)
其中u表示简谐波的波速,在传播中t时刻的振动速度为
(10)
质点在此时刻的振动动能为
(11)
弦线因发生弹性形变而具有弹性势能,则质点的弹性势能为
(12)
质点的机械能为动能和势能之和,即
(13)
单位体积介质中所具有的波的能量称为能量密度,形成驻波的两列简谐波即入射波和反射波的能量密度分别为
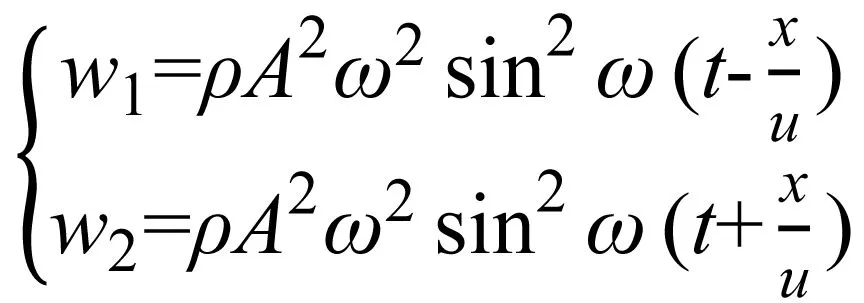
(14)
其中ρ为弦线的线密度,两波叠加后形成的驻波的能量密度[3]为
(15)
1) 波腹、波节处的能量密度
2) 相邻波腹、波节之间的动能和势能
(1) 相邻波腹、波节之间的动能:驻波中质点的动能密度为
(16)
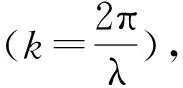
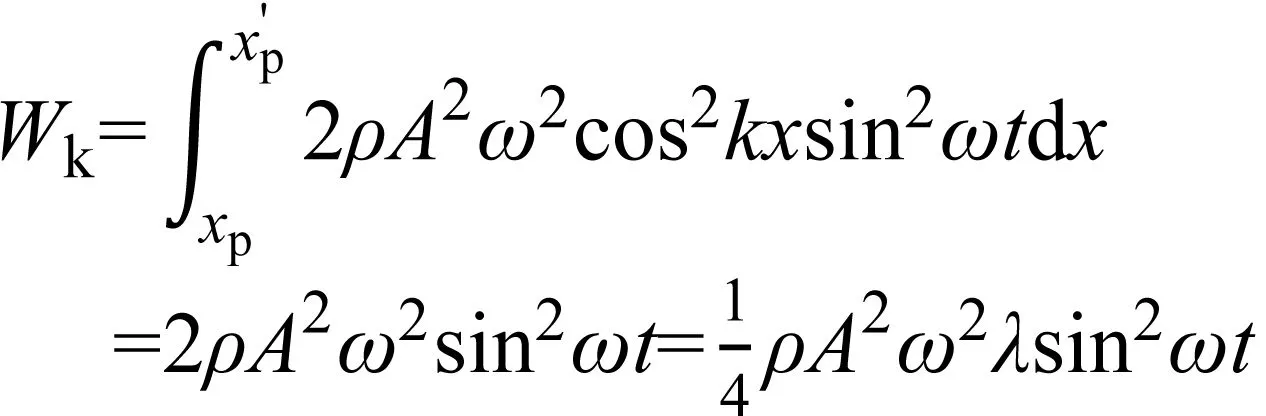
(17)
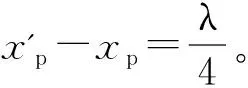
(2) 相邻波腹、波节之间的势能:质点的势能密度为
wp=w-wk=2ρA2ω2sin2kxcos2ωt
(18)
同理,对(18)式积分可得相邻波腹波节之间的势能
(19)
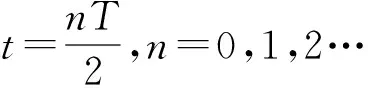
综上可知,当介质中所有质点的位移达到最大值时,各质点速度为零,即动能为零,这时除了波节外,所有质点都不在其平衡位置,从而引起介质的最大弹性形变,此时驻波上各个质点的全部能量都是势能,因为波节附近的相对形变最大,所以势能最大,而在波腹附近相对形变为零,所以势能为零,从波腹到波节势能逐渐增大,能量以势能形式集中在波节附近。同理,当介质中所有质点同时达到平衡位置时,介质的形变为零,因此势能也为零,这样驻波的全部能量都是动能。这时波腹处各个质点的速度最大,即动能最大;而在波节处各个质点速度为零,即动能为零,此时能量以动能形式集中在波腹附近,由此可见,介质在振动过程中,驻波的能量在相邻波腹和波节之间往复变化,在相邻波节间动能和势能不断地进行转换,且在转换过程中能量不断地由波腹附近转移到波节附近,再由波节附近转移到波腹附近,这也说明了在驻波进行的过程中没有能量的定向传播。
2 弦上驻波
在传统的物理课本中,通常是利用上述理论推导出理想驻波方程,但弦振动上的驻波[4]有别于无限空间的理想驻波,从现象上看,仔细观察会发现弦线上“驻波”的波节处并非静止在其平衡位置上;从理论上看,弦线上的入射波和反射波在传播过程中总是存在着机械能的损耗,并且在反射端处也有能量损失。因此,相干波的振幅并不是常量。如果将相干波的振幅为常量时所形成的驻波称为理想的驻波时,那么,相干波的振幅不相同或为变量时所形成的驻波,则可以通称为实际的驻波。
2.1 弦线上的驻波实验
弦线上驻波的实验通常采用一端固定的拉紧的弦线来演示,在跨过滑轮的弦线的一端系一砝码,在弦线的另一端接一电动音叉,如图1所示。电动音叉在弦线上激起行波,此时行波的频率就是电动音叉的频率。电动音叉激发的余弦波自A端入射,进入AB弦向右传播,到达端点B,由于B端保持固定不动,波就被反射回来传到A端,受音叉端面反射又返回去,如此往返的传播形成驻波,所以这本质上是一个求解无限多正反向传播余弦波的合成问题。基于这个思路,本文给出弦振动形成的波动的一般表达式,这与严格意义的理想驻波表示相近。
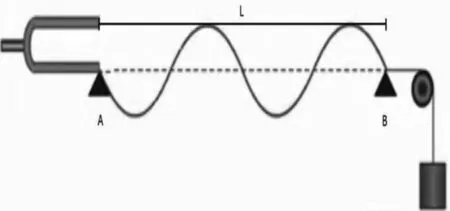
图1 弦上驻波实验
2.2 弦线上驻波形成的条件
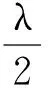
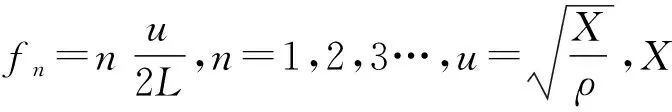
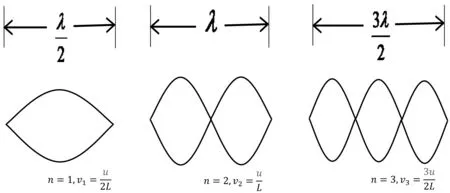
图2 两端固定的简正模式
2.3 半波损失
在图1所示的实验中,反射点B是固定的,且在此处形成驻波的一个波节。这说明当反射端固定时,绳子会产生一个与入射波反向的扰动即反射波,两波在B点处是反相位的。如果反射端是自由的,那么受到绳子的扰动会形成一个和入射波在B点处相位相同的入射波,那么形成的驻波在B点处应该是波腹,也就是说,当反射点固定不动的时候,反射波和入射波间发生相位突变,因为相距半波长的两质点相位差为π,而波程差为半个波长,所以这个相位突变称为半波损失,如果反射点是自由的,那么反射波和入射波相位相同,此时反射波和入射波之间不存在相位突变。
根据研究表明,当波从波疏媒质垂直入射到波密媒质界面上反射时,有半波损失,形成的驻波在界面处是波节。当波从波密媒质垂直入射到波疏媒质界面上反射时,无半波损失,界面处出现波腹。
2.4 弦线上驻波的方程
为了比较理想的驻波与实际的驻波之间的差别及各自的特点,下面分4种情况分析讨论弦线上的驻波。
1) 部分反射波
弦线上的驻波是由入射波和反射波的叠加而成。其中反射波[6]可能有两种情况:第一种是波从波疏媒质向波密媒质传播,则在B点反射时,有半波损失;第二种是波从波密媒质向波疏媒质传播,则反射时无半波损失。
设入射波t时刻在A点的振动方程为yA=Acosωt,且波方程为
y1=Acos(ωt-kx)
(20)
该波传播到B点处,在B处的振动方程为
yB=Acos(ωt-kL)
(21)
当波从波疏媒质向波密媒质传播,在B点反射时有半波损失,此时振动方程为
yB′=Acos(ωt-kL+π)
(22)
反射波向左传播L距离后,在A点的振动方程为
yA′=Acos(ωt-2kL+π)
(23)
则反射波以A点为原点的波方程为
y2=Acos(ωt-2kL+π+kx)
(24)
(25)
为了更直观地看清楚结果,本文运用Mathematica软件中Plot命令绘制出驻波形成的曲线,另外除自变量外还有一些参数,这些参数的大小需通过可交互式的调节,本文运用Manipulate命令来实现参数调节操作,在上述条件下可知,两波存在初相位差π ,因此通过调节相位φ来实现,得到如图3所示的三条振动曲线,其中细虚线为入射波,粗虚线为反射波,实线为合成的驻波。
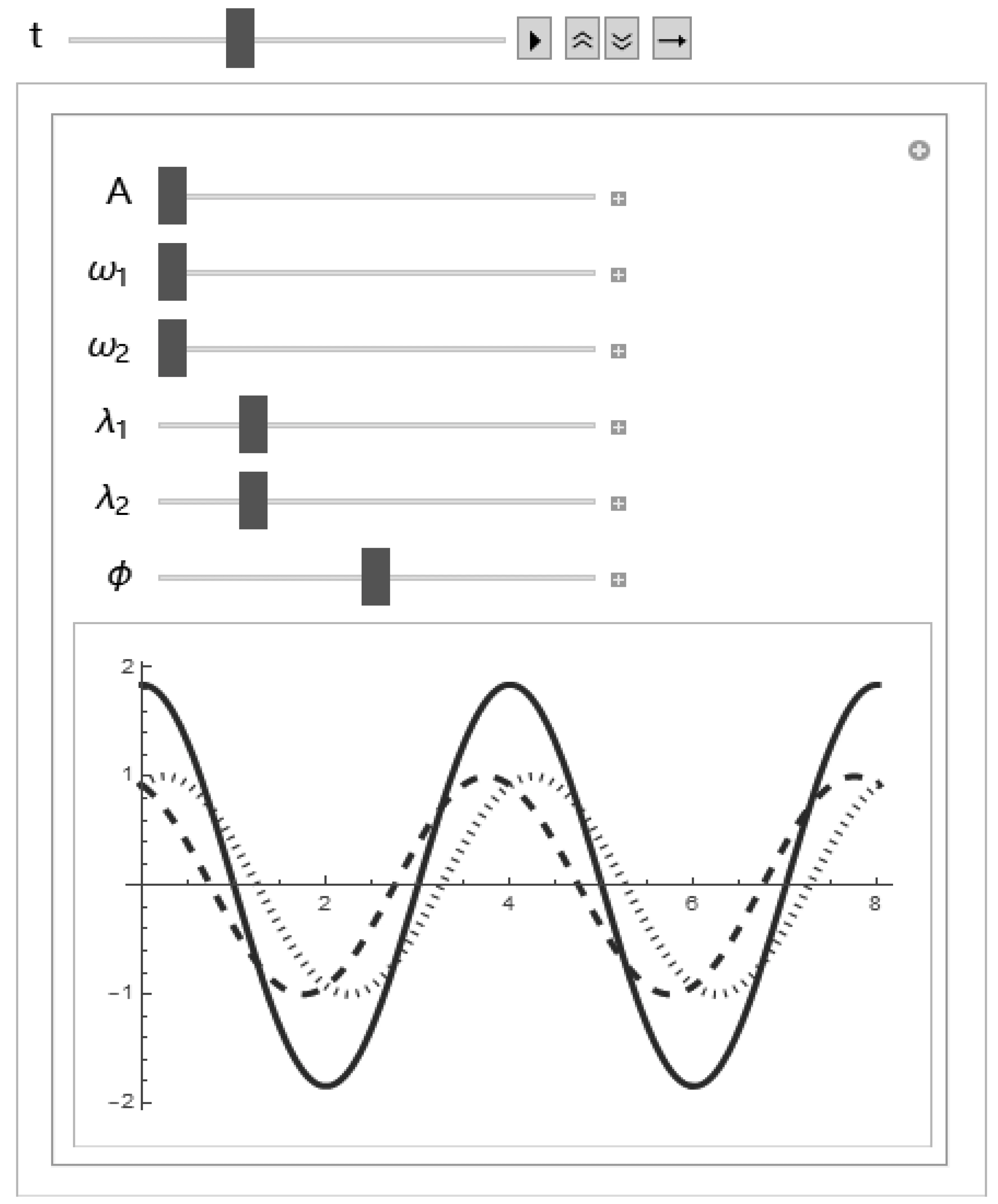
图3 部分反射波形成的驻波
2) 完全反射波
当波从波密媒质向波疏媒质传播,在B点反射时无半波损失,此时振动方程为
yB″=Acos(ωt-kL)
(26)
反射波向左传播L距离后,在A点的振动方程为
yA″=Acos(ωt-2kL)
(27)
则反射波以A点为原点的波方程为
(28)
(29)
上述条件下描述的是没有半波损失的条件,因此我们可以在Mathematica中,调节参数使得两波初始相位相同,从而得到如图4的三条振动曲线,其中细虚线为入射波,粗虚线为反射波,实线为合成的驻波。
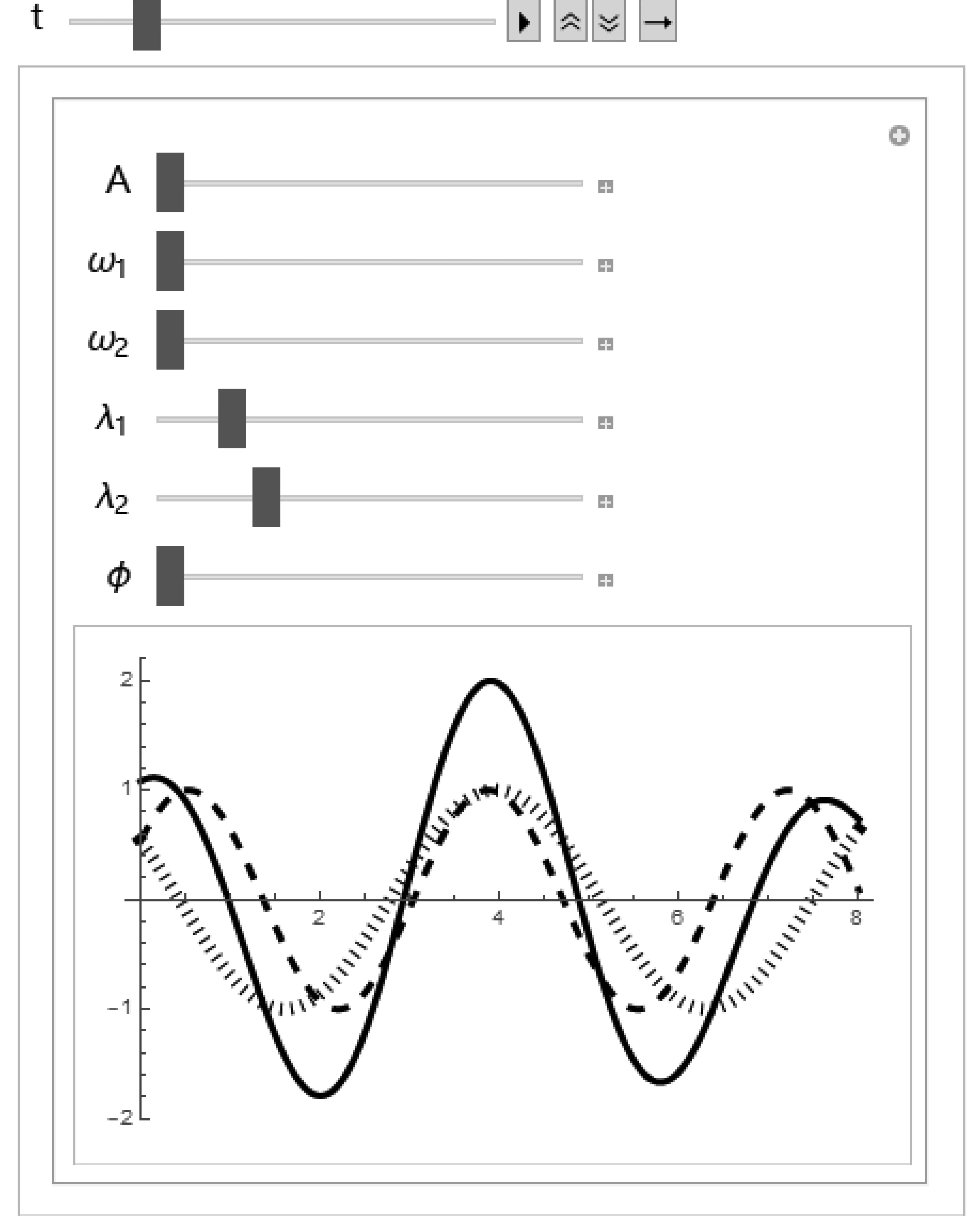
图4 完全反射波形成的驻波
3) 弦线为吸收介质
实际上,波在向前传播过程中媒质对它的吸收总是程度不同的存在着。如果考虑到行波在弦线上传播时的能量损失[7],则在弦线上所形成的驻波又有两种情况。第一种情况反射波为完全反射;第二种情况反射波为部分反射。
首先分析第一种情况,如果入射波方程为y1=Ae-αx)cos(ωt-kx),式中α为介质的吸收系数,则反射波的波方程为
y2=Ae-α(2L-x)cos(ωt-2kL+kx)
(30)
这样形成的驻波方程为
y=y1+y2=Ae-αxcos(ωt-kx)+Ae-α(2L-x)cos(ωt-2kL+kx)
(31)
当考虑到波在弦线上传播的过程中存在能量损失时,我们可以在直接在Mathematica中修改波的方程,将吸收系数作为参数,通过调节各个参数的取值大小,这里我们假设吸收系数的取值范围为1~2,得到如图5所示的三条振动曲线,其中细虚线为入射波,粗虚线为反射波,实线为合成的驻波。
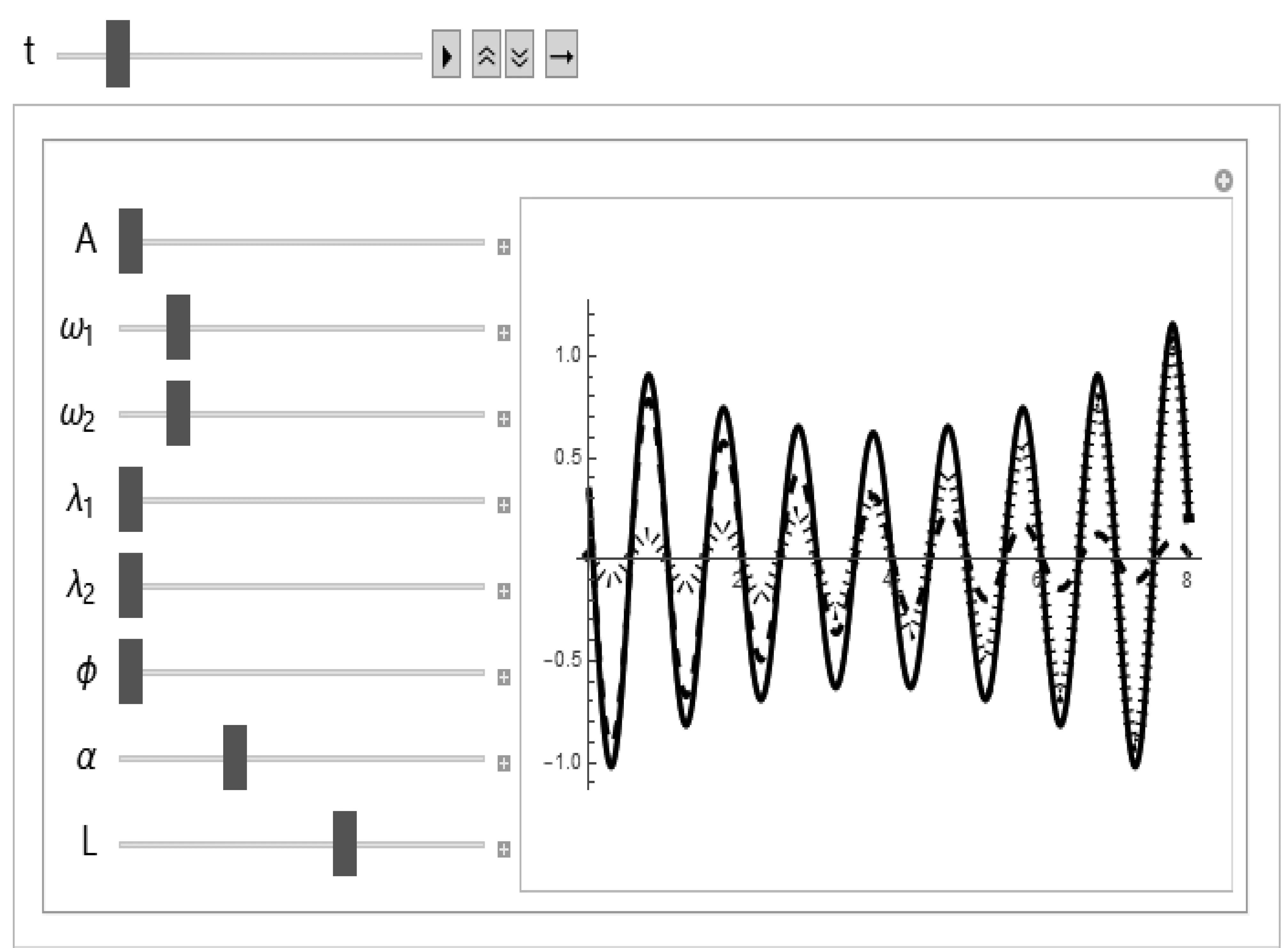
图5 完全反射条件下弦线为吸收介质的波的曲线图
4) 实际弦线上的驻波
我们所看到弦线上的驻波,既存在行波传播过程中的能量损失,在固定端又是存在半波损失。此时,若入射波的波方程为
y1=Ae-αxcos(ωt-kx)
(32)
设反射系数为f1,反射波的波方程为
y2=f1Ae-α(L-x)cos(ωt-kL+π+kx)
(33)
向左传播的y2波传至音叉处,又经过A反射,此时反射波方程为
y3=f1f2Ae-α(2L-x)cos(ωt-2kL+kx)
(34)
f2为音叉的反射系数,2kL表示y3比y1相位落后,设f1、f2为不随L和波形变化的定值,则可类似的得到反射波y4…
此时,驻波的波方程为
y=y1+y2+y3+…=Ae-αxcos(ωt-kx)+f1Ae-α(L-x)cos(ωt-kL+π+kx)+f1f2Ae-α(2L-x)cos(ωt-2kL+kx)+…
(35)
通过分析,我们可以知道实际情况下弦上驻波既存在能量损失,又存在半波损失,所以我们需要把吸收系数和初相位这两个关键的参数都进行调节,使其满足上述条件。此时由Mathematica软件[8]画出的曲线如图6所示,其中细虚线为入射波,粗虚线为反射波,实线为合成的驻波。
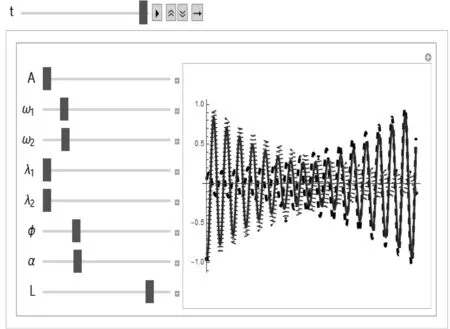
图6 实际情况下弦上驻波的曲线图
3 结语
本文首先从驻波理论的基础开始,利用干涉的概念推导出理想驻波的方程,在此基础上讨论了波节、波腹的位置以及相位分布,然后根据弹性理论知识讨论了驻波的能量密度;其次是驻波的应用,利用弦线上的驻波实验,找到了驻波形成的条件同时也推导出简正模式下简正频率的取值;最后为了更深入的理解驻波方程,本文综合考虑行波传播过程中的能量损失和在固定端存在半波损失两个因素,最终得出实际弦线上驻波的方程,并且运用了Mathematica中的一些命令将不同条件下驻波的形成进行了较为直观的演示,这对电学领域中交流电、电磁波在电气电子工程应用中有很大的参考意义。
