磁耦合共振无线能量传输系统中平面螺旋线圈的设计

李闻先,田小建,尤 元

(1.吉林大学 电子科学与工程学院,长春 130012;2.长春工业大学 电气与电子工程学院,长春 130012)

利用磁耦合共振无线能量传输可点亮2 m内的一只60 W灯泡,其传输效率为40%[1],文献[2]实现了在0～80 cm内以70%以上的效率为负载供电,目前无线充电技术已引起人们广泛关注[3-6].传统电磁感应式无线能量传输系统中的螺旋线圈通常作为电感,需采用串联或并联电容补偿,利用数学方法计算其电感值.平面螺旋天线利用其电感与分布电容形成等效的谐振回路,通过Neumann公式计算电感值,但其分布电容值的计算较复杂,且分布电容值随频率的变化而变化[7].本文采用电磁仿真软件(FEKO)计算平面螺旋线圈的近场值,通过扫频设置可求得近场值与频率的关系,从而得到平面螺旋线圈的谐振频率.根据仿真数据制作平面螺旋线圈,利用网络分析仪测试其S11参数,测试结果与仿真结果相符,表明该方法正确.

1 平面螺旋线圈的等效模型及电感计算

1.1 平面螺旋线圈的等效模型 平面螺旋线圈由电感与线圈间的分布电容及导线电阻组成,可等效为一个LC串联电路,磁耦合共振系统的等效电路模型如图1所示.

1.2 计算平面螺旋线圈的自感 为简化计算平面螺旋线圈的自感,将平面螺旋电感的几何结构单元简化为如图2所示的模型.

图1 磁耦合共振系统等效电路模型Fig.1 Equivalent circuit model of the magnetically coupled resonance system

图2 平面螺旋线圈简化模型单元Fig.2 Simplified model unit of planar spiral coil

线圈Ci和Cj的磁通量可表示为

(1)

根据Neumann公式[8]可得

(2)

将各分量代入式(2)可得

(3)

将式(3)化简为[7]

(4)

由式(4)可求得平面螺旋线圈的自感为

(5)

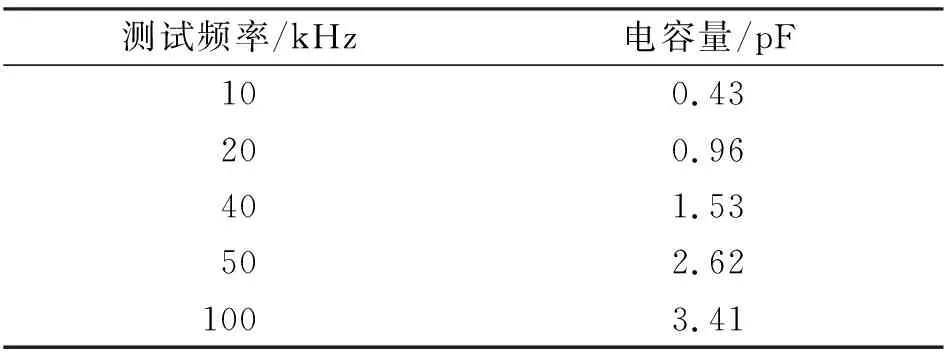
表1 平面螺旋线圈电容的测试结果Table 1 Capacity test results of planar spiral coil

1.3 测量平面螺旋线圈的分布电容 由于平面螺旋线圈的分布电容随频率的变化而变化[7],因此不易计算其分布电容.本文采用TH2817A型LCR数字电桥测试了一种线圈模型,测试结果列于表1.由表1可见,相同螺旋线圈在不同频率下的分布电容变化较大,因此不易设计一定谐振频率的螺旋线圈.

2 平面螺旋线圈的设计与仿真计算

图3 平面螺旋线圈的几何模型Fig.3 Geometry model of planar spiral coil

本文采用一种用于3D结构电磁场分析的仿真软件FEKO,在FEKO中建立的3D模型如图3所示.该线圈内径19.5 cm,外径30 cm,匝数N=10,导线直径1.2 mm,采用同轴线馈电.激励频率为10～30 MHz扫频,激励源功率为10 W.

对线圈z轴正半轴(法向)50 cm处面积为1 m2的区域电场进行仿真计算,计算结果如图4所示,其中图4(A)为频率与电场强度的变化关系曲线,图4(B)为线圈50 cm处1 m2区域范围内的电场强度计算结果.由图4(A)可见,当频率为18.8 MHz时,电场强度E的最大值为49.96 kV/m;由图4(B)可见,由于各个线圈产生的电场相互叠加,电场强度的最大值点并未在平面螺旋线圈的中心.

3 实验结果比较

根据实验仿真的几何模型,采用手工方法制作平面螺旋线圈,使用厚度为1.5 mm的Acrylic板作为线圈骨架,采用六块矩形Acrylic板嵌入骨架内部,在矩形Acrylic板上均匀挖出凹槽以便固定线圈.制作成型后可通过改变矩形凹槽在骨架的位置调节平面螺旋线圈的几何结构,从而进行线圈的调试工作.制作实物如图5所示.

使用美国Agilent公司生产的E5061A型网络分析仪测试平面螺旋线圈的S11参数,测试结果如图6所示.

图5 制作的平面螺旋线圈Fig.5 Design of planar spiral coil

由图6可见,该平面螺旋线圈的谐振频率为19.3 MHz,软件仿真结果为18.8 MHz,仿真与实测结果基本相符.其中误差主要由以下原因产生:

1) 由于制作工艺水平有限,因此制作的线圈几何结构与仿真几何结构存在一定的误差;

2) 仿真计算为真空环境下的结果,由于Acrylic板及线圈上的塑料外皮均为具有一定介电常数的介质,因此对电磁场有一定的影响;

3) 线圈内径与仿真结果存在一定的误差,从而影响谐振频率.

本文使用设计制作的平面螺旋天线搭建了一套磁耦合共振无线能量传输系统,该系统在30 cm处点亮一组高亮LED阵列,系统可为50 Ω负载提供的峰值电压约为14.7 V.根据

可求得传输功率为2.16 W,其传输效率大于50%.

综上,本文设计并研究了应用于磁耦合共振无线能量传输系统中的平面螺旋线圈特性,可得如下结论：

1) 采用电磁仿真软件(FEKO)对平面螺旋线圈的近场进行仿真计算,得出其谐振频率,解决了采用传统电路模型不易计算线圈分布电容的难题,并降低了设计的计算量；通过实验测试结果与仿真结果的对比,验证了仿真计算的准确性.

2) 通过无线能量传输实验,验证了采用该方法设计制作平面螺旋线圈的可行性.

[1] Kurs A,Karalis B,Moffatt R,et al.Wireless Power Transfer via Strongly Coupled Magnetic Resonances [J].Science,2007,317: 83-86.

[2] Sample A P,Meyer D A,Smith J R.Analysis,Experimental Results,and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer [J].IEEE Transactions on Industrial Electronics,2011,58(2): 544-554.

[3] Imura T,Okabe H,Hori Y.Basic Experimental Study on Helical Antennas of Wireless Power Transfer for Electric Vehicles by Using Magnetic Resonant Couplings [C]//Vehicle Power and Propulsion Conference.Dearbon: [s.n.],2009: 936-940.

[4] CHEON Sang-hoon,KIM Yong-hae,KANG Seung-youl,et al.Circuit-Model-Based Analysis of a Wireless Energy-Transfer System via Coupled Magnetic Resonances [J].IEEE Transactions on Industrial Electronics,2011,58(7): 2906-2914.

[5] LUAN Hui,ZHANG Hong-wu,ZHAO Kai.Research of Microwave Radiometer Receiver Calibration [J].Journal of Jilin University: Science Edition,2007,45(3): 458-462.(栾卉,张洪武,赵凯.微波辐射计接收机的定标方法 [J].吉林大学学报: 理学版,2007,45(3)：458-462.)

[6] WANG Sheng-yuan,ZHANG Hong-wu,ZHAO Kai,et al.Design and Realization of Wireless Transceiver Module in Communication of Many Machines [J].Journal of Jilin University: Science Edition,2006,44(3): 469-472.(王胜源,张洪武,赵凯,等.无线收发模块在多机通信中的设计与实现 [J].吉林大学学报: 理学版,2006,44(3)：469-472.)

[7] WANG Xin,WANG Zong-xin,YUAN Xiao-jun.Calculation of Self-inductance and Distributed Capacitance of Spiral Inductor [J].Research &Progress of SSE,2000,20(4): 424-432.(王昕,王宗欣,袁晓军.圆形螺旋线圈自感和分布电容的计算 [J].固体电子学研究与进展,2000,20(4): 424-432.)

[8] Chan H L,Cheng K W E,Sutanto D.A Simplified Neumann’s Formula for Calculation of Inductance of Spiral Coil [C]//Eighth International Conference on Power Electronics and Variable Speed Drives.London: [s.n.],2000: 69-73.