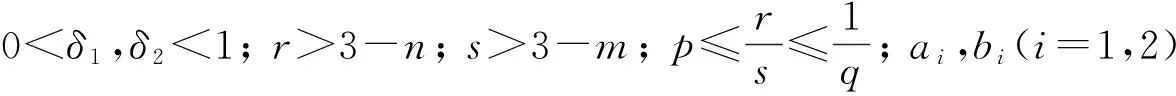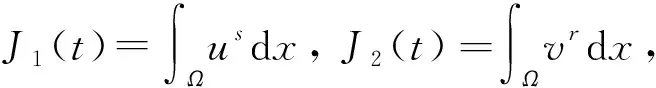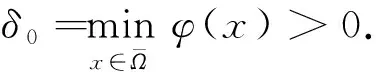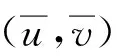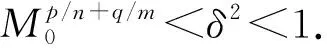具非线性源快扩散方程组解的熄灭
2013-12-03王国铭朱立勋
刘 令,王国铭,朱立勋
(1.吉林建筑大学 基础科学部,长春 130118;2.吉林大学 数学学院,长春 130012)
0 引 言
考虑如下快扩散方程组解的熄灭性质:
(1)
其中: 0
与解的有限时刻爆破一样,解的有限时刻熄灭也是发展型方程的一个重要性质.自从Kalashnikov[4]通过比较Cauchy问题:
对于如下形式的非线性扩散方程:
(2)
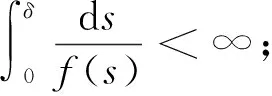
具有非线性源项的快扩散方程
(3)
解的熄灭性质也得到了广泛研究,其中0 陈玉娟等[3]考虑了当N>2时问题(1)解的熄灭性质,先证明了该问题弱解的局部存在性及某些特殊情形时弱解的唯一性,然后借助常微分方程组不变区域理论和积分估计的技巧,对某些特殊情形证明了当初值u0与v0“可比”时,该问题的解在有限时刻熄灭.基于此,本文研究问题(1)当N=1,2时解的性质.通过改进文献[3]使用的方法,对更广泛的源函数给出了问题(1)的解在有限时刻熄灭的充分条件.本文使用的方法不仅可以处理低维情形,还可以极大简化高维情形时类似结论的证明.由于问题(1)的反应项当0 当m,n>1时,问题(1)是退化的;而当0 定义1如果向量值函数(u,v)∈L∞(QT)×L∞(QT)满足下列3个条件,由称其为问题(1)在QT上的一个弱下解(弱上解): 1)u(x,0)≤(≥)u0(x),v(x,0)≤(≥)v0(x),x∈Ω; 2)u(x,t)≤(≥)0,v(x,t)≤(≥)0,(x,t)∈ΓT; 3) 对任意的t∈(0,T)和任意的ξ,η∈F, 如果(u,v)既是弱上解,又是弱下解,则称(u,v)是问题(1)在QT上的一个弱解. 问题(1)弱解的局部存在性可通过标准正则化方法证明[19],本文仅简述其过程.考虑如下正则化问题: (4) 选取T>0充分小,使得对任意的k∈,问题(4)在QT上存在唯一正解(uk,vk),且‖uk‖L∞(QT)+‖vk‖L∞(QT)关于k是一致有界的.事实上,对任意的k∈,常微分方程Cauchy问题: (5) 的解是问题(4)的一个上解.只需选取T>0为问题(5)解的最大存在区间即可.此外,由一致抛物型方程组解的比较原理可知,如果k 类似地有 (7) 定义有界函数Φk,Fk,Ψk和Gk,使其满足: 则式(6)和式(7)可改写为 ∬Qt(u-uk){ξs+ΦkΔξ}dxds+∬Qtξ(v-vk)Gkdxds, 用类似于文献[19]的方法选取恰当的检验函数ξ,η并借助Gronwall不等式可得(u,v)≤(uk,vk),从而有(u,v)≤(U,V).故(U,V)是问题(1)的最大解. 下面建立问题(1)在某些特殊情形下解的唯一性.令λ1>0和φ1(x)分别是如下特征问题的第一特征值和相应的特征函数: -Δφ(x)=λφ(x),x∈Ω;φ(x)=0,x∈∂Ω. (8) 选取φ1(x)>0,将其单位化,使得‖φ1‖L∞(Ω)=1. 命题1如果下述条件之一成立,则问题(1)的局部解是唯一的: 1)q>m且p>n; 2)q>m,p=n且λ1≥1; 3)p>n,q=m且λ1≥1; 4)q=m,p=n且λ1≥1. 证明: 当条件4)成立时,问题(1)的解是唯一的[3].因此只需证明情形1)~3).令(u,v)是问题(1)的任意解,(uk,vk)是问题(4)的解,选取φ1(x)作为检验函数可得 令k→∞,得 ∬Qt{-λ1(Um-um)+(Vp-vp)}φ1(x)dxds. (9) 类似地有 ∬Qt{-λ1(Vn-vn)+(Uq-uq)}φ1(x)dxds. (10) 先考虑q>m且p>n的情形.由文献[21]可知,存在M>0和常数0 (11) 命题2假设(u,v)和(z,w)分别是问题(1)在QT上的非负弱上、下解,且存在δ>0,使得(u,v)≥(δ,δ),则(u,v)≥(z,w)于QT. 命题2的证明过程类似证明(U,V)是问题(1)的最大解,故略. 为方便,将‖·‖Lα(Ω)简记为‖·‖α. 引理1[3]设ai,bi(i=1,2),p,q是正常数,0 其中0<δ1,δ2<1.假设非负函数W1,W2满足 (12) 如果(W1(0),W2(0))∈Q,则(W1,W2)∈Q. 引理2[3]假设引理1的条件成立,则当(W1(0),W2(0))∈Q时,问题(12)的任意非负解都是单调不增的,且在有限时刻熄灭. 由引理2和常微分方程组的比较原理可得如下推论. 推论1假设非负函数W1,W2满足 (13) 如果(W1(0),W2(0))∈Q,则问题(13)的任意非负解(W1,W2)在有限时刻熄灭. 定理1假设mn (14) 证明: 为方便,不妨假设问题(1)的弱解具有很好的光滑性.否则可以对正则化问题的解得到相应的估计,然后通过标准极限过程得到所需的结论.由于pq≤1,易知此时存在常数r,s>1,使得p≤r/s≤1/q.在问题(1)的方程两端分别乘以us-1,vr-1后在Ω上分部积分,可得 (15) (16) (17) 这里γ1>0是嵌入常数.将式(17)代入式(15)可得 (18) (19) 类似地可得 (20) 其中:r>3-n;γ2>0是嵌入常数.令 则由式(19)和式(20)可得 (21) 对式(21)应用推论1可知,当初值(u0,v0)满足式(14)时,(W1,W2)在有限时刻熄灭,从而(u,v)也在有限时刻熄灭.证毕. 定理2假设mn<1 (22) 其中: 0<δ1,δ2<1;p1∈(0,p)满足mn 证明: 由于mn -Δφ(x)=1,x∈Ω0,φ(x)=0,x∈∂Ω0, (23) 于是,式(15),(16)可分别改写为 (24) (25) 这里p1∈(0,p)满足mn 定理3假设mn=pq且区域Ω适当小,则对适当小的初值(u0,v0),问题(1)至少存在一个在有限时刻熄灭的解. 证明: 通过构造一个在有限时刻熄灭的上解完成证明.为此,令 令(g1(t),g2(t))是下述常微分方程组的非负解: (26) 本文使用的方法也可处理具非局部源的快扩散方程组解的熄灭性质. [1] Vazquez J L.The Porous Medium Equation [M].Oxford: Clarendon Press,2007. [2] Bebernes J,Eberly D.Mathematical Problem from Combustion Theory [M].New York: Springer-Verlag,1989. [3] CHEN Yu-juan,WANG Juan,ZHANG Hai-xing.Extinction for a Couple of Fast Diffusion Systems with Nonlinear Sources [J].Nonl Anal: Real World Applications,2013,14(4): 1931-1937. [4] Kalashnikov A S.The Nature of the Propagation of Perturbations in Problems of Non-linear Heat Conduction with Absorption [J].USSR Comp Math Math Phys,1974,14(4): 891-905. [5] Diaz G,Diaz I.Finite Extinction Time for a Class of Non-linear Parabolic Equations [J].Comm Part Differ Equations,1979,4(11): 1213-1231. [6] Lair A V,Oxley M E.Extinction in Finite Time of Solutions to Nonlinear Absorption-Diffusion Equation [J].J Math Anal Appl,1994,182(3): 857-866. [7] Galaktionov V A,Vazquez J L.Asymptotic Behavior of Nonlinear Parabolic Equations with Critical Exponents.A Dynamical System Approach [J].J Funct Anal,1991,100(2): 435-462. [8] Galaktionov V A,Vazquez J L.Extinction for a Quasilinear Heat Equation with Absorption Ⅰ.Technique of Intersection Comparison [J].Comm Part Dier Equations,1994,19(7/8): 1075-1106. [9] Galaktionov V A,Vazquez J L.Extinction for a Quasilinear Heat Equation with Absorption Ⅱ.A Dynamical System Approach [J].Comm Part Dier Equations,1994,19(7/8): 1107-1137. [10] Ferreira R,Vazquez J L.Extinction Behavior for Fast Diffusion Equations with Absorption [J].Nonl Anal: Theory,Methods &Applications,2001,43(8): 943-985. [11] Friedman A,Herrero M A.Extinction Properties of Semilinear Heat Equations with Strong Absorption [J].J Math Anal Appl,1987,124(2): 530-546. [12] Herrero M A,Velzquez J J L.Approaching an Extinction Point in One-Dimensional Semilinear Heat Equations with Strong Absorptions [J].J Math Anal Appl,1992,170(2): 353-381. [13] Lair A V.Finite Extinction Time for Solutions of Nonlinear Parabolic Equations [J].Nonl Anal: Theory,Methods &Applications,1993,21(1): 1-8. [14] GU Yong-geng.Necessary and Sufficient Condition of Extinction of Solutions on Parabolic Equations [J].Acta Mathematica Sinica,1994,37(1): 73-79.(顾永耕.抛物型方程的解熄灭(Extinction)的充要条件 [J].数学学报,1994,37(1): 73-79.) [15] LI Yu-xiang,WU Ji-chun.Extinction for Fast Diffusion Equations with Nonlinear Sources [J].Electron J Differ Equations,2005,2005(23): 1-7. [16] TIAN Ya,MU Chun-lai.Extinction and Non-extinction for ap-Laplacian Equation with Nonlinear Source [J].Nonl Anal: Theory,Methods &Applications,2008,69(8): 2422-2431. [17] YIN Jing-xue,JIN Chun-hua.Critical Extinction and Blow-up Exponents for Fast Diffusivep-Laplacian with Sources [J].Math Method Appl Sci,2007,30(10): 1147-1167. [18] HAN Yu-zhu,GAO Wen-jie.Extinction for a Fast Diffusion Equation with a Nonlinear Nonlocal Source [J].Arch Math,2011,97(4): 353-363. [19] Anderson J R.Local Existence and Uniqueness of Solutions of Degenerate Parabolic Equations [J].Commun Partial Differential Equations,1991,16(1): 105-143. [20] Potter M H,Weinberger H F.Maximum Principle in Differential Equations [M].Englewood Cliffs: Prentice-Hall,1967. [21] Anderson J R.Necessary and Sufficient Conditions for the Unique Solvability of a Nonlinear Reaction-Diffusion Model [J].J Math Anal Appl,1998,228(2): 483-494.1 弱解的局部存在与唯一性
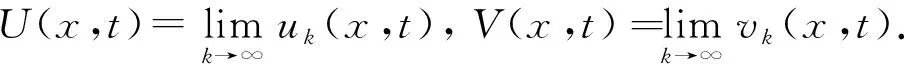
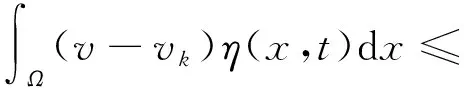

2 主要结果