野草算法优化提取广义切比雪夫滤波器耦合矩阵

田雨波， 马 远

(江苏科技大学 电子信息学院，江苏 镇江 212003)

随着现代通信技术的发展,通信系统对微波滤波器的性能指标及体积大小提出了越来越严格的要求.广义切比雪夫滤波器通过引入有限频率的传输零点,在不增加滤波器阶数的同时,能有效提高滤波器的性能,因此被广泛应用于各种微波通信系统中.文献[1-2]中分别提出了N阶及N+2阶耦合矩阵的综合理论,但是提取出来的耦合矩阵对应的拓扑结构很难直接用于工程实际中,需要根据实际的拓扑结构对其进行相似变换.由此可见,如何提取出可行的耦合矩阵是广义切比雪夫滤波器设计的重点及难点.传统的矩阵相似变换方法只能适用于特定的拓扑结构,很难推广使用,故而采用智能优化方法得到任意拓扑结构的耦合矩阵.文献[3]给出单纯形法和梯度法相结合的方案来提取耦合矩阵,文献[4]采用粒子群算法优化提取广义Chebyshev线性相位滤波器耦合矩阵,以上两种方法均为直接优化滤波器的传输函数之法,因而对初始值的选取比较敏感.

野草算法(invasive weeds optimization,IWO)是一种模拟杂草繁殖过程的新型的随机搜索仿生学优化算法[5].IWO算法自2006年提出以来,得到了广泛的应用,并显现出强大的优势和潜力,在电磁学领域内亦获得了应用[6-10].文中采用野草算法,在电路综合理论的基础上,优化旋转矩阵的角度,以实现广义切比雪夫滤波器耦合矩阵的消元.最后,依据提取的耦合矩阵设计微波滤波器,并给出相应的测试结果.

1 野草算法基本理论及改进

IWO是受野草启发而提出的、基于种群的数值优化计算方法,其主要执行过程有如下4个步骤:

1)初始化种群.对一些参数进行初始化设置:问题的维数D,随机初始化G个杂草植株,最大迭代次数itermax,最大种群数目Pmax,最大和最小可生成种子数Smax和Smin,非线性指数n,区间步长初始值σinit和最终值σfinal及初始搜索空间X.

2)生长繁殖.繁殖过程按照自然界中的繁殖法则,给予不可行的个体较小的生存和繁殖的机会,根据适度值及种群所有个体的最小和最大适度值来确定种群中的成员能够播散的种子数,计算公式如下:

Num(i)=

seedmin

(1)

式中：seedmax和seedmin为最大和最小种子数,BestFitness和WorstFitness为族群种子的最好和最差适度值,fitness(i)为族群中第i个种子的适度值.

3)空间扩散.产生的种子个体按照正态分布在其父代杂草个体附近的D维空间进行扩散,选取的正态分布均值为0,标准差为σcur.每轮迭代对应不同的标准差,随着迭代的进行,标准差从σinit开始至σfinal结束.σcur计算公式如下:

(2)

4)竞争排斥.通过数代的繁殖后,后代的数目将超过环境资源的可承受能力.通过最大种群数目Pmax对种群数量进行控制.在算法迭代过程中,种群中的所有杂草和其后代按适度值从大到小依次排序.取适度值最优的前Pmax个个体,其余个体将被去除.

根据上述野草算法的主要步骤使用MATLAB编程实现,具体的算法流程如图1.

图1 野草算法流程Fig.1 Flowchart of IWO

2 广义切比雪夫滤波器耦合矩阵的相似变换

文献[1]详细介绍了综合法提取广义切比雪夫滤波器耦合矩阵的方法.综合方法得到的广义切比雪夫滤波器耦合矩阵一般来说无法直接使用,因为耦合矩阵的元素都是非零元素.由于耦合矩阵的特征值决定了滤波器的传输和反射特性,只要保证耦合矩阵的特征值不变,滤波器的频率响应特性就不会改变.根据矩阵理论,对矩阵进行相似变换,即在不改变矩阵特征值的前提下,对矩阵的元素作消零处理.

一个N阶耦合矩阵M0的相似变换,是通过在M0的左边和右边分别乘以N阶旋转矩阵R及其转置矩阵RT来实现的:

M1=R·M0·RT

(3)

式中：M0为初始矩阵,M1为相似变换后的矩阵.6阶旋转矩阵R(支点为[3,5],旋转角度为θ)如式(3)定义,其中cr=cos(θ),sr=sin(θ).

(4)

用野草算法控制每次旋转的角度,目标函数取为耦合矩阵中需要消去的元素值模之和,通过不断的迭代,使目标函数不断变小.当小于某个特定值时,可以认为其为零,从而实现了消元.使用MATLAB编程实现,程序流程如图2.

图2 野草算法优化提取耦合矩阵程序流程Fig.2 Flow chart of IWO to extract the coupling matrix

3 数值实验

为了验证用野草算法来优化提取任意拓扑结构的耦合矩阵的有效性,给出了4种拓扑结构(图3).下面以第一种拓扑结构为例,详细介绍优化提取的整个过程,并通过其他3种结构来进一步验证此种方法的通用性.由于实际问题中,源或负载直接与中间腔体耦合的情况很少,以因此以N阶耦合矩阵的优化提取为例.

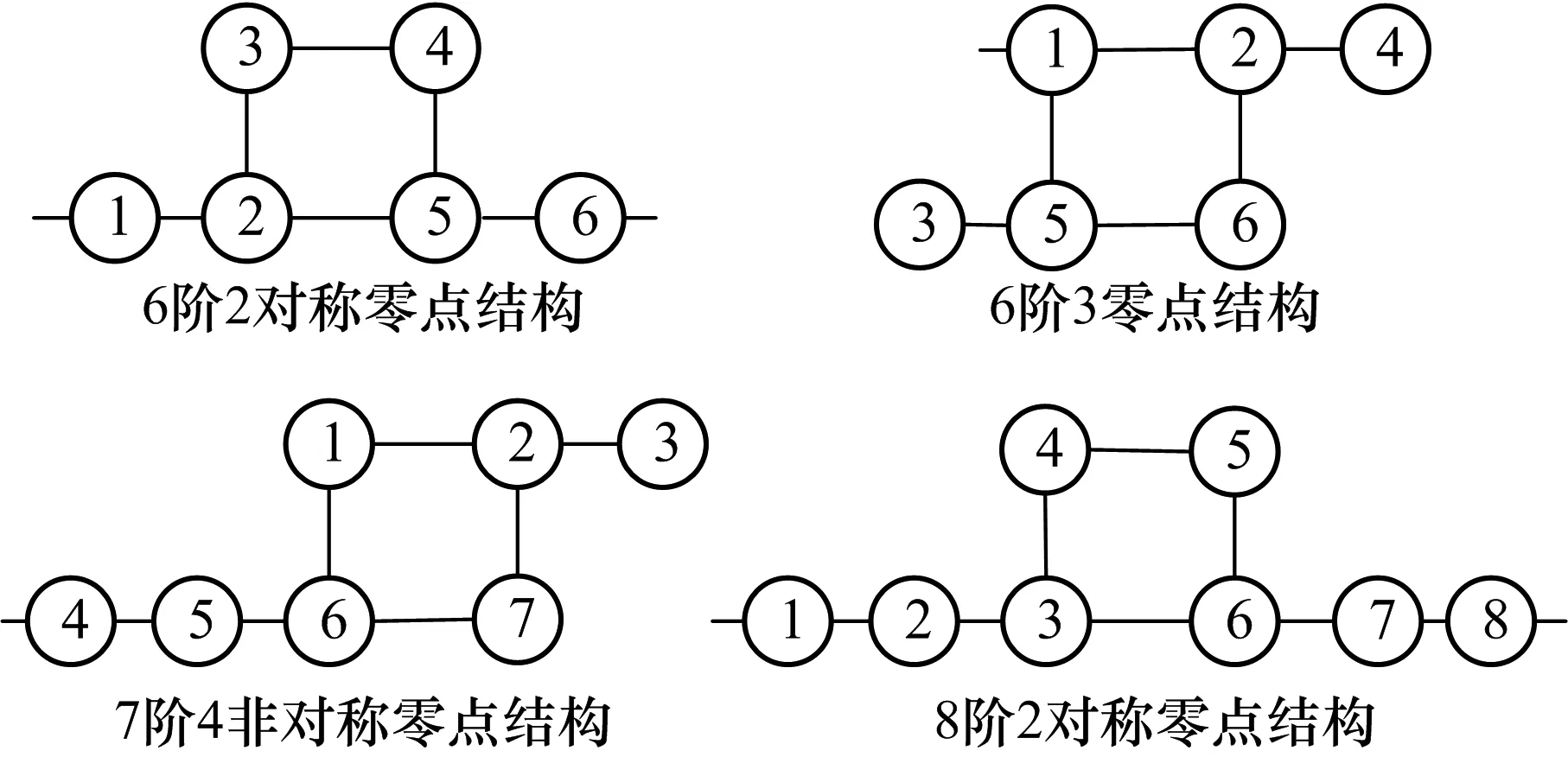
图3 4种拓扑结构示意Fig.3 4 kinds of topological structure diagram

例1 6阶2对称传输零点结构,传输零点位置为j2和-j2.

为了实现消元,需要6个旋转矩阵,它们的旋转点分别为(2,3),(2,4),(2,5),(3,4),(3,5)和(4,5),所以问题的维数为6维,每一维的优化参量对应着每一个旋转矩阵的旋转角度,初始值取(-4,4)之间的随机数.每次旋转公式如下:

(5)

由图3所示结构可以看出,这种结构最终的耦合矩阵应有如下形式:

(6)

所以设定算法的目标函数为:

goal=abs(m13)+abs(m14)+abs(m15)+

abs(m16)+abs(m24)+abs(m26)+abs(m35)+

abs(m36)+abs(m46)

(7)

通过对每次旋转角度的优化,来实现目标函数的归零,从而达到消元的目的.

用MATLAB编程实现野草算法对耦合矩阵的消元.表1给出IWO算法相关参数.经优化后,目标函数值为1.877 5e-004,趋近于0,可认为实现了消元.最终得到耦合矩阵为:

M=

表1 IWO算法的参数设定值Table 1 IWO algorithm parameter settings

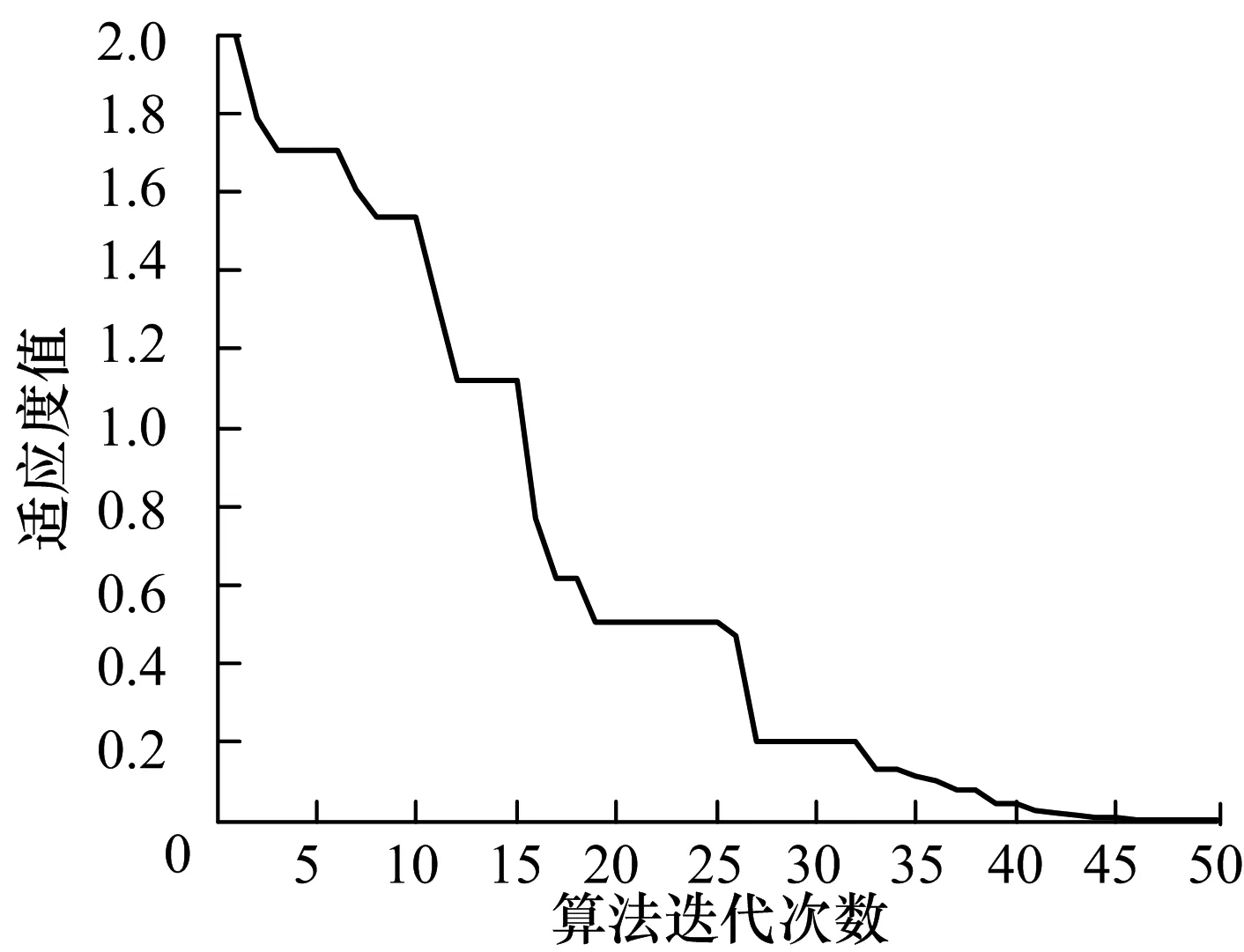
图4 IWO算法收敛过程Fig.4 Convergence process of the IWO algorithm

从图4可见,经过50次迭代计算,结果收敛,而实际计算时间小于2 min,收敛速度较快.图5为根据提取出来的耦合矩阵计算的对应拓扑结构的广义切比雪夫滤波器的归一化幅频响应,其中S11是反射函数,S21是传输函数,.由图可见,传输零点的位置与预先设定的传输零点的位置基本吻合,并且滤波器所对应的拓扑结构为图3中的第一种结构,是物理可实现的.

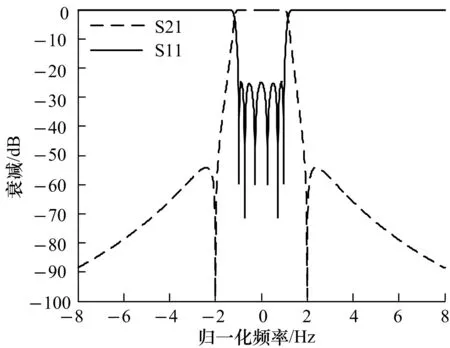
图5 6阶2对称零点结构归一化幅频响应Fig.5 Normalized amplitude-frequency response of the 6 order 2 symmetric transmission zero structure

例2 6阶3非对称传输零点结构,传输零点位置:j1.5,j3,-j2.

目标函数设置为:

goal=abs(m13)+abs(m14)+abs(m16)+

abs(m23)+abs(m25)+abs(m34)+

abs(m45)+abs(m46)

(8)

得到耦合矩阵:M=

图6 6阶3非对称零点结构归一化幅频响应Fig.6 Normalized amplitude-frequency response of the 6 order 3 asymmetric zero structure

从图6可看出,最终归一化幅频响应上的3个不对称零点与预先设定值是一致的.

例3 7阶4非对称传输零点结构,传输零点位置:j1.5,j3,j5,-j2.

因为滤波器的阶数由6阶增加为7阶,所以算法的维数增加至10维,并且根据消元的位置,新的目标函数为:

goal=abs(m13)+abs(m14)+abs(m15)+

abs(m17)+abs(m24)+abs(m25)+abs(m26)+

abs(m35)+abs(m36)+abs(m37)+

abs(m46)+abs(m47)+abs(m57)

(9)

最终得到耦合矩阵为:

M=

图7 7阶4非对称零点结构归一化幅频响应Fig.7 Normalized amplitude-frequency response of the 7 order 4 asymmetric zeros structure

例4 8阶2对称传输零点结构,传输零点位置:-j1.3,j1.3.

目标函数设置为:

goal=abs(m13)+abs(m14)+abs(m15)+

abs(m16)+abs(m17)+abs(m18)+abs(m24)+

abs(m25)+abs(m26)+abs(m27)+abs(m28)+

abs(m35)+abs(m36)+abs(m37)+abs(m38)+

abs(m46)+abs(m47)+abs(m48)+abs(m57)+

abs(m58)+abs(m68)

(10)

R1=RN=0.973 9.

图8显示了根据上述M矩阵计算得到的归一化原型的幅频响应.

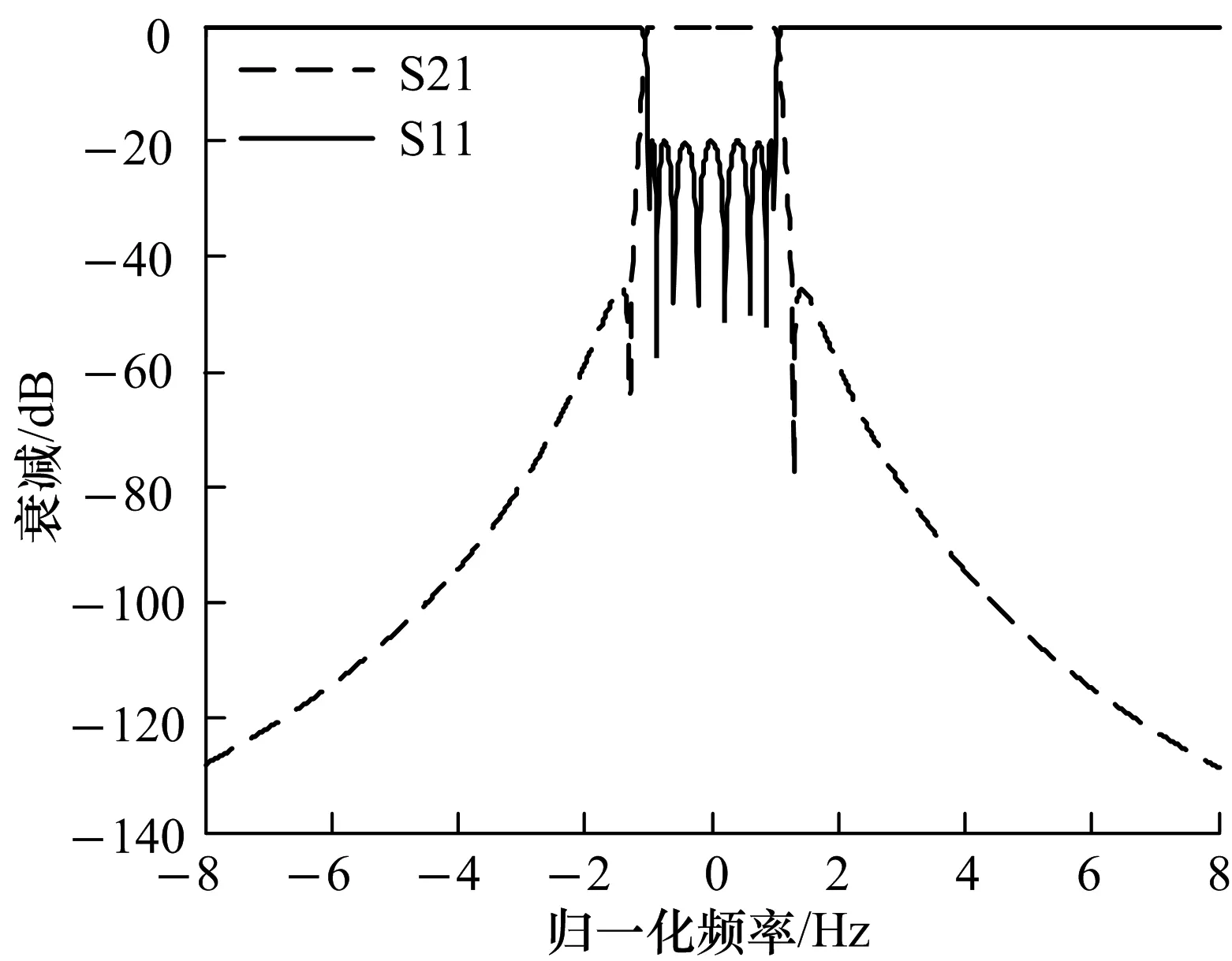
图8 8阶2对称零点结构归一化幅频响应Fig.8 Normalized amplitude-frequency response of the 8 order 2 symmetric zeros structure

从以上4例可以看出,对任意的拓扑结构,使用野草算法来优化提取耦合矩阵,经过迭代,都能得到良好的收敛效果,实现了较快的收敛速度和较好的收敛精度,并且优化结果不依赖于算法初值的选取,预先设定的传输零点的位置与所提取出的耦合矩阵的传输函数的零点位置基本吻合,得到耦合矩阵对应的广义切比雪夫滤波器在物理上是可实现的.

4 微波滤波器的设计及实测结果

以例4提取出的耦合矩阵,设计8阶微带滤波器,设计过程采用HFSS电磁仿真软件来实现.滤波器中心频率为5 GHz,带宽400 MHz,要求在偏离中心频率500 MHz处的带外抑制优于-60 dBc.选取介电常数为2.2的罗杰斯5880板材来实现,板厚0.5 mm,覆铜厚度0.02 mm.各谐振器的具体尺寸位置利用HFSS本征模求解器依据耦合矩阵计算得到,如图9.在HFSS仿真软件中建立相应的模型,仿真结果如图10,满足设计指标要求.按照设计的滤波器结构尺寸加工实物,如图11,矢量网络分析仪的测试结果如图12.从图12可以看出,滤波器的带外拟制效果比较理想,在偏离中心频点±500 MHz处均优于-65 dBc.由于采用了带插针的SMA接头,插针焊接不是很好,故通带内回波损耗最差点达到-10 dB.由于微带线的Q值不是很高,滤波器的插入损耗比较大.

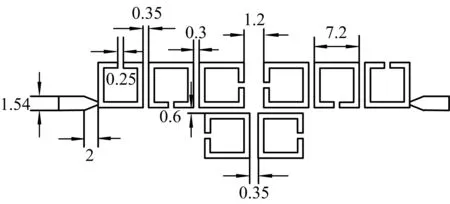
图9 滤波器结构(单位：mm)Fig.9 Filter structure(Unit:mm)

图10 HFSS仿真结果Fig.10 HFSS simulation results

图11 实物照片Fig.11 Real photos

图12 测试结果Fig.12 Test results

5 结论

使用优化方法提取广义切比雪夫滤波器耦合矩阵,不受滤波器拓扑结构的影响,具有较大的灵活性.文中用野草算法对广义切比雪夫滤波器耦合矩阵进行了优化提取,在电路综合理论提取耦合矩阵的基础上,使用优化算法来优化矩阵相似变换的角度,对任意的拓扑结构只需要改变相应的目标函数.相比直接用旋转的方法来消元,程序简单并更具通用性.MATLAB编程实验结果表明,这种方法很好地完成了广义切比雪夫滤波器任意结构耦合矩阵的提取.文中以优化提取的耦合矩阵为基础,利用HFSS电磁仿真软件设计交叉耦合滤波器,经实物加工测试,得到了理想的结果,验证了该方法的可行性.使用野草算法优化提取耦合矩阵,对于不同的拓扑结果只需修改优化的目标函数,无需重新编写程序,从而提高了滤波器的设计效率,具有一定的工程实用价值.

[1] Cameron R J.General coupling matrix synthesis methods for Chebychev filtering function[J].IEEETransactionsonMicrowaveTheoryandTechnology,1999,47(4):433-442.

[2] Cameron R J.General coupling matrix synthesis techniques for microwave filters[J].IEEETransactionsonMicrowaveTheoryandTechnology,2003,51(6):1-10.

[3] 韩世虎,王锡良,樊勇.广义切比雪夫滤波器耦合矩阵的优化提取[J].电波科学学报,2007,22(1):153-157.

Han Shihu,Wang Xiliang,Fan Yong.Optimization method for extracting coupling matrix of generalized chebyshev filter[J].ChinaResearchInstituteofRadioWavePropagation,2007,22(1):153-157.(in Chinese)

[4] 闭万毅,龚盈颖,张耀方,等.广义Chebyshev线性相位滤波器耦合矩阵的优化提取[C]∥2009年全国微波毫米波会议论文集(上册).[S.l.]:中国电子学会微波分会,2009.

Bi Wanyi,Gong Yingying,Zhang Yaofang,et al.Optimization method for extracting coupling matrix of generalized Chebyshev linear phase filter[C]∥The2009NationalConferenceOnMicrowaveandMillimeterWave,MicrowaveBranchofChineseInstituteofElectronics,2009.(in Chinese)

[5] Mehrabian A R,Lucas C.A novel numerical optimization algorithm inspired from weed colonization[J].EcologicalInformatics,2006,1(4):355-366.

[6] 韩毅,蔡建湖,李延来,等.野草算法及其研究进展[J].计算机科学,2011,38(3):20-23.

Han Yi,Cai Jianhu,Li Yanlai,et al.Invasive weed optimization and its advances[J].ComputerScience,2011,38(3):20-23.(in Chinese)

[7] 柏艳英.方向图可重构天线单元及其在阵列中的应用研究[D].四川成都:电子科技大学,2012.

[8] Mohamadi F M,Nader K,Mousavi P.Application of invasive weed optimization to design a broadband patch antenna with symmetric radiation pattern[J].IEEEAntennasandWirelessPropagationLetters,2011,10: 1369-1372.

[9] Ghosh R G,Swagataml D,Prithwish C,et al.Design of Non-Uniform circular antenna arrays using a modified invasive weed optimization algorithm[J].IEEETransactionsonAntennasandPropagation,2011,59(1): 110-118.

[10] Sedighy S H,Ali-Reza Reza M,Mohammad S,et al.Optimization of printed yagi antenna using invasive weed optimization[J].IEEEAntennasandWirelessPropagationLetters,2010,9: 1275-1278.