强迫位移式门式刚架的强迫位移量确定方法
2013-11-19唐柏鉴张福星
唐柏鉴,张福星,马 珺
(江苏科技大学 土木工程学院,江苏 镇江 212003)
门式刚架轻钢结构在国内发展迅速,应用范围已由中、低跨度建筑扩展到大跨度建筑[1].但是随着门式刚架跨度的增大和竖向荷载的增加,斜梁弯矩峰值增加,导致梁的内力很不均匀[2].门式刚架跨中设置摇摆柱并将预应力技术引入门式刚架,可以有效改善门式刚架的受力性能,降低斜梁弯矩峰值[3-4].在此基础上文中提出了强迫位移式门式刚架结构(图1),即对中柱的几何长度故意“缩短”Δ.安装门式刚架时,通过强迫位移法[5]完成中柱与斜梁的连接,从而实现在门式刚架中施加预应力.
如何确定强迫位移量Δ是该结构的关键问题.强迫位移式门式刚架的实质是以强迫位移产生的预应力调节荷载作用下的构件内力,使得构件的内力更为均匀.文中依据强迫位移的期望作用——限制位移并调节弯矩,建立了强迫位移量确定理论.
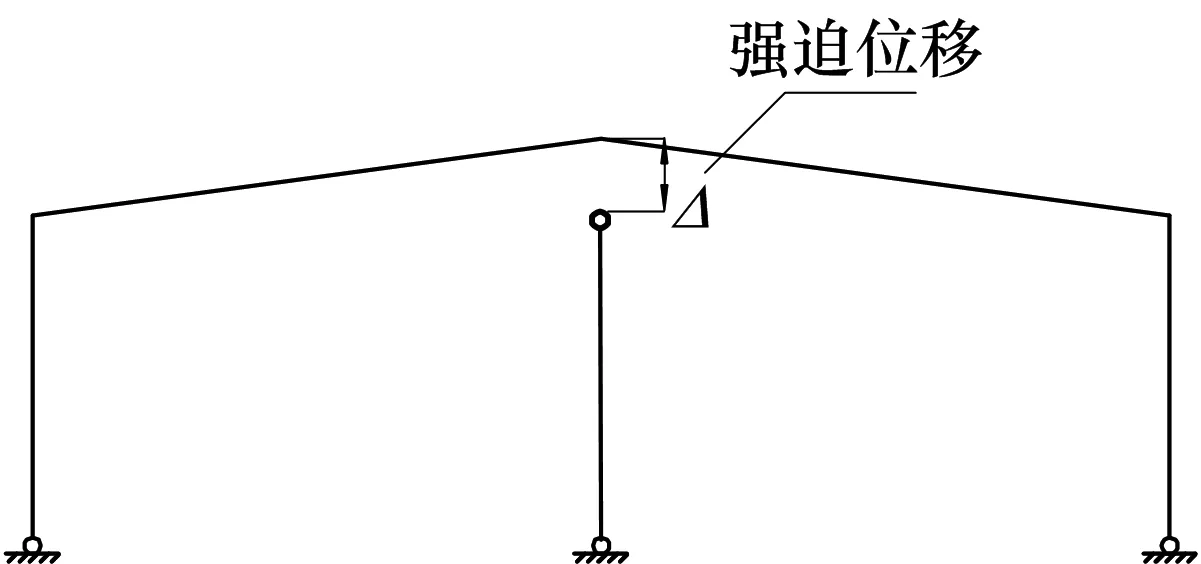
图1 强迫位移式门式刚架Fig.1 Forced displacement portal frame
1 强迫位移式门式刚架强迫位移量的确定准则及理论
强迫位移式门式刚架结构中,不仅摇摆柱限制刚架跨中位移,而且强迫位移产生的预应力能够改善梁的内力分布.根据“在外部竖向荷载作用下,屋脊弯矩与梁柱连接处或斜梁跨中截面弯矩绝对值相等,构件内力分布达到最均匀状态”的原则,得出强迫位移量确定方法.
1.1 关于刚架计算的基本公式[6]
图2为单层单跨柱脚铰接的等截面门式刚架.刚架跨度为L,柱高为h,柱截面惯性矩Ic,梁截面惯性矩Ib,斜梁长度为s,檐口到屋脊的垂直距离为f.刚架的长高比:λ=L/h,ψ=f/h;刚度分配系数:k=h/s×Ib/Ic;刚度修正系数:μ=3+k+ψ(3+ψ).(图中,1,2为斜梁与柱连接处;3,4为斜梁跨中处;5为屋脊处)
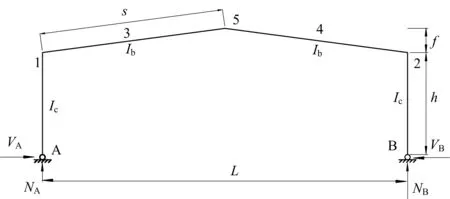
图2 刚架的几何尺寸Fig.2 Geometrical size of portal frame
1)均布荷载作用下的刚架内力及变形
荷载相关系数:

(1)
(2)
2)梁上集中荷载P作用下
荷载相关系数:
弯矩方程:
(3)

(4)
1.2 有摇摆柱的门式刚架的内力及变形计算
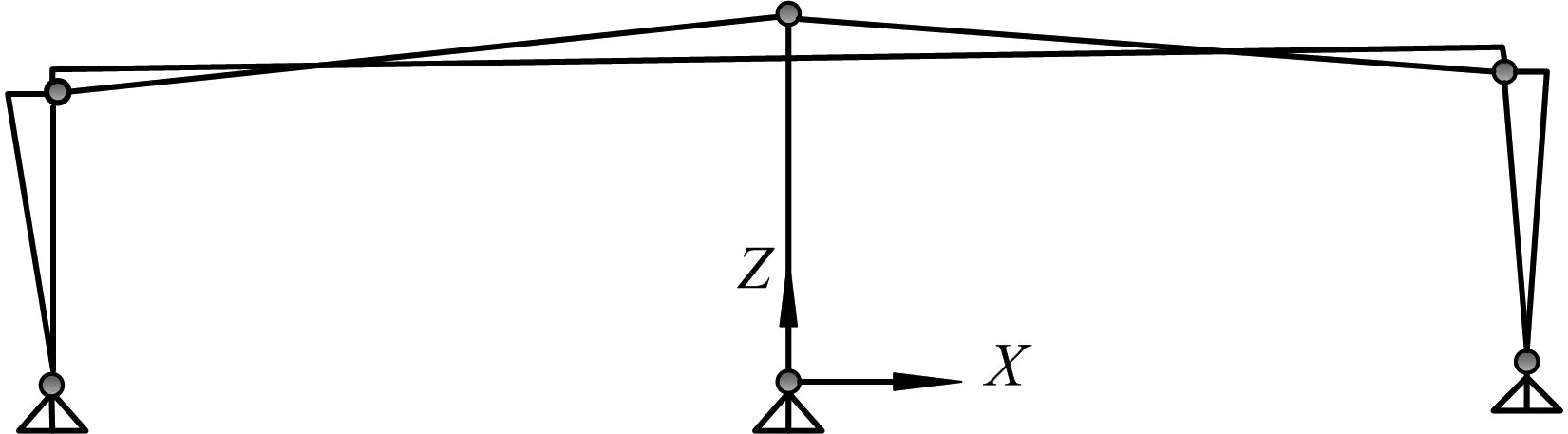
铰接于框架梁的摇摆柱中只存在轴力且轴向刚度较大,与强迫位移量相比,摇摆柱的轴向变形量非常小.因此在竖向荷载作用下忽略摇摆柱的轴向变形,摇摆柱可视为刚性杆.摇摆柱对门式刚架的作用简化为集中力Nsc施加于门式刚架(图3).
由于存在摇摆柱,屋脊挠度为零,根据变形协调关系得:
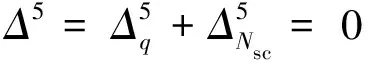
(5)
(6)

图3 有摇摆柱的门式刚架受力叠加Fig.3 Force superimposition of portal frame with swing column

(7)
由单跨门式刚架在均布荷载作用下的弯矩叠加其在反力Nsc作用下的弯矩得到刚架梁弯矩:
梁柱连接处弯矩:

(8)
斜梁跨中弯矩:

(9)
屋脊处弯矩:
(10)
由式(8~10)可知,由于摇摆柱的反力作用,屋脊产生了很大的负弯矩,梁端头弯矩大大降低甚至小于屋脊弯矩,斜梁跨中弯矩可能增大也可能减小.总体上梁内力分布不均匀,可采用强迫位移法来调整.
1.3 强迫位移量的确定
强迫位移法的实质是以强迫位移作用下的内力图形去调整荷载作用下的内力图形,使得构件的内力分布更为均匀.图4分别是刚架在竖向荷载作用下、强迫位移作用下和两者叠加后的弯矩图.由此可见,强迫位移作用下的结构受力满足叠加原理,并且叠加后的刚架梁内的弯矩峰值有效减小[7].

a)竖向荷载作用
b)强迫位移作用
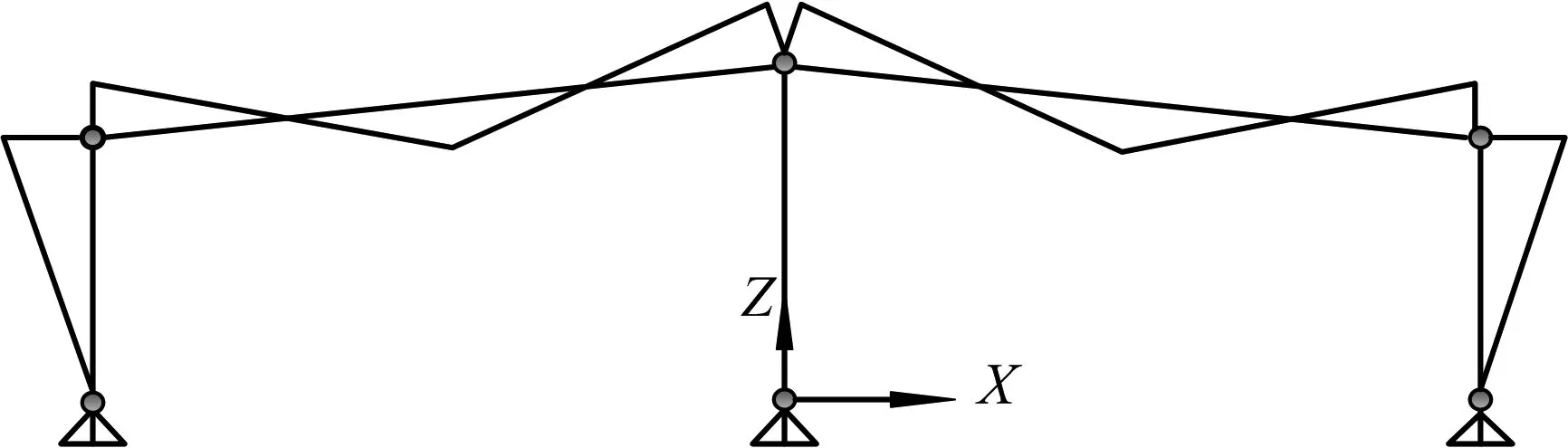
c)竖向荷载和强迫位移共同作用
通常情况下,斜梁的用钢量大于柱.随着跨度的增加,斜梁用钢量所占的比重加大.因此,对斜梁进行优化可以取得较好的经济效益.当强迫位移量达到某一值时,屋脊弯矩与梁柱连接处弯矩或斜梁跨中截面弯矩绝对值相等,构件内力分布达到最均匀状态.这一位移值就是位移优化值[8-9].设在强迫位移作用下摇摆柱轴力为Nscg,得梁柱连接处弯矩为:
(11)
斜梁跨中弯矩为:

(12)
屋脊处弯矩为:
(13)

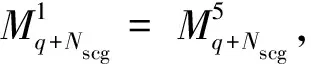
(14)
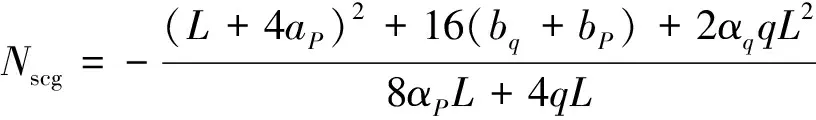
(15)
根据叠加原理,设置强迫位移后,在荷载作用下摇摆柱的轴力NP为:

(16)
对刚架跨中施加向下的拉力NP,并将其铰接于摇摆柱顶.由于摇摆柱轴向刚度较大,其轴向变形可忽略,因此由于结构变形导致的初始张拉力损失可忽略不计.使用千斤顶施加拉力,千斤顶的初始张拉力即为NP.
忽略摇摆柱在竖向荷载作用下的轴向变形,施加的强迫位移量就等于刚架跨中受向下拉力NP作用下的挠度:

(17)
刚架梁最大弯矩减小量:

(18)
2 结论
1)强迫位移式门式刚架结构中,强迫位移量可以产生预应力.荷载作用下的内力与强迫位移作用下的内力叠加,从而调匀斜梁内力分布.以屋脊弯矩与梁柱连接处或斜梁跨中截面弯矩相等为强迫位移量的确定准则.
2)根据上述准则及叠加原理,建立了强迫位移量的计算公式,以及屋脊弯矩减小量的计算公式.
[1] 中国工程建设标准化协会.门式刚架轻型房屋钢结构技术规程[S].北京:中国计划出版社,2002.
[2] 周国良,赵希平.轻钢厂房设计中一些问题的探讨[J].钢结构,2001,16(6): 32-33.
Zhou Guoliang,Zhao Xiping.Discussion on some problems in the design of light steel plant[J].SteelStructure,2001,16(6): 32-33.(in Chinese)
[3] 朱晶晶,唐柏鉴,渠延模.预应力技术在轻型门式刚架中的应用[J].钢结构,2009,24(1): 5-7.
Zhu Jingjing,Tang Baijian,Qu Yanmo.Application of pre-stressed technology in light portal frame[J].SteelStructure,2009,24(1): 5-7.(in Chinese)
[4] 顾建飞.预应力门式刚架的受力性能研究[D].浙江杭州:浙江大学,2006:51-52.
[5] 唐柏鉴,马珺,王治均.201210387878.6 采用支座位移法施加预应力的预应力钢框架及其施工方法[P].北京:中国知识产权局,2012.
[6] 包头钢铁设计研究总院.钢结构设计与计算 [M].北京:机械工业出版社,2006:83-112.
[7] Kim S E,Choi S H,Kim C S.Automatic design of space steel frame using practical nonlinear analysis[J].Thin-WalledStructures,2004,42: 1273-1291.
[8] 刘鹏.门式刚架的优化设计[J].工业建筑,2001,31(7): 58-60.
Liu Peng.Optimization design of portal frames[J].IndustrialBuilding,2001,31(7): 58-60.(in Chinese)
[9] 柳锋,郭兵,陈长兵,等.门式刚架的经济尺寸与优化初设计[J].钢结构,2003,18(l): 32-34.
Liu Feng,Guo Bing,Chen Changbing,et al.Economic dimension and optimized initial design in portal frame[J].SteelStructure,2003,18(1): 32-34.(in Chinese)
