问题2555的另证、推广及拓展
2021-05-12陕西省岐山县蔡家坡高级中学722405公宽让
陕西省岐山县蔡家坡高级中学(722405) 公宽让
1 问题2555 的另证
题目设正实数a,b,c满足abc≥1,证明:
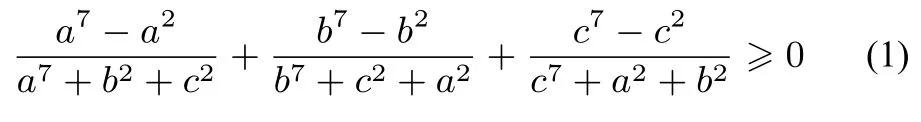
这是《数学通报》2020年7月号问题中的不等式问题2555,作者在第8 期的证明中多次应用均值不等式,构思奇妙,但不易推广.下面用切比雪夫不等式和均值不等式对问题2555 给出另证.
证明a,b,c >0,且abc≥1,不妨设a≥b≥c >0,由切比雪夫不等式和均值不等式,

令= 7, 得r=<7.即同理,求和, 得(∑表示对a,b,c循环求和),故
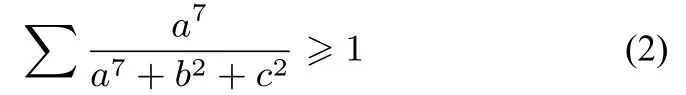
再由切比雪夫不等式和均值不等式,
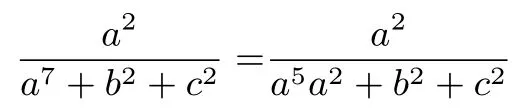
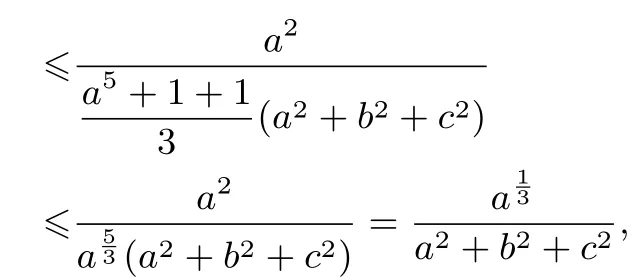
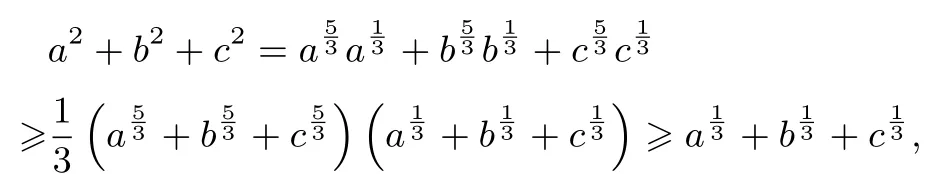
所以a2+b2+c2≥即=1,故
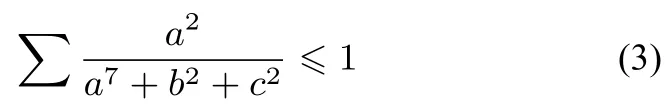
不等式(2)与不等式(3)相减,即得不等式(1)成立.
2 问题2555 的推广
2.1 问题2555 按项数推广
定理1 已知ai >0(i= 1,2,...,n,n≥3,n ∈N+),且为对ai(i=1,2,...,n)循环求和,则

2.2 问题2555 按项数和指数推广
定理2已知ai >0(i= 1,2,...,n,n≥3,n ∈N+),且,k ∈N+,∑为对ai(i=1,2,...,n)循环求和,则
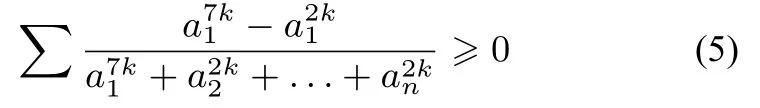
为了方便下面的证明,先给出一个引理.
引理已知ai >0(i= 1,2,...,n,n≥3,n ∈N+),且则

证明ai >0(i= 1,2,...,n,n≥ 3,n ∈N+), 且不妨设a1≥a2≥...≥an >0,由切比雪夫不等式和均值不等式,
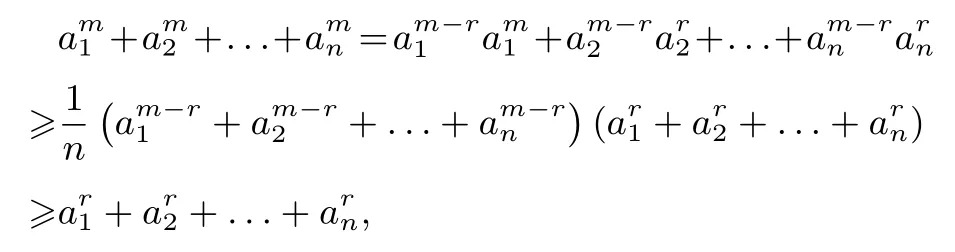
所以,不等式(*)成立.
下面证明定理1、定理2.
证明ai >0(i= 1,2,...,n,n≥ 3,n ∈N+) 且≥1,k ∈N+, 不妨设a1≥a2≥...≥an >0, 由切比雪夫不等式和均值不等式,

令r+=7k,得r=<7k.即同理
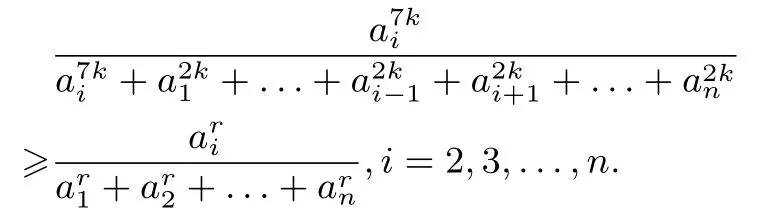
求和,得
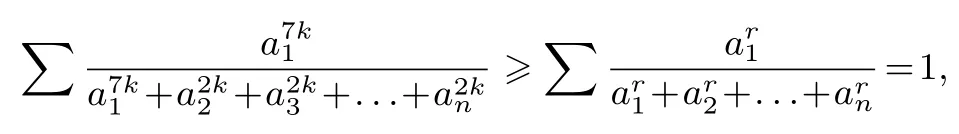
故
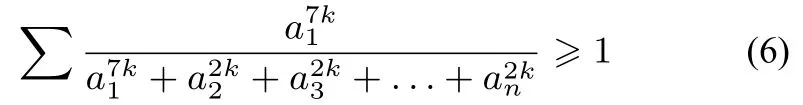
再由切比雪夫不等式和均值不等式,


求和,得
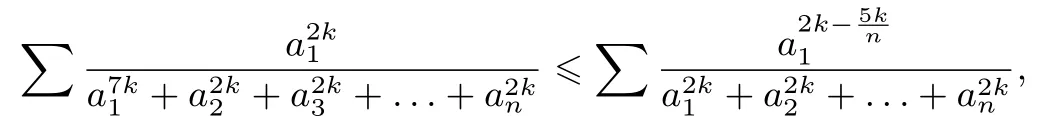
由不等式(*),得
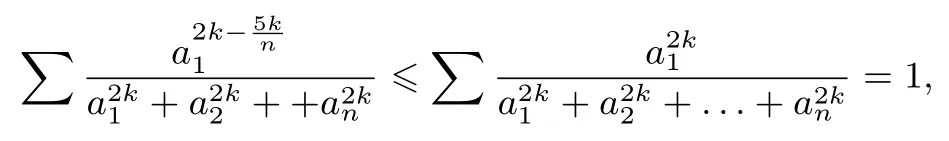
故
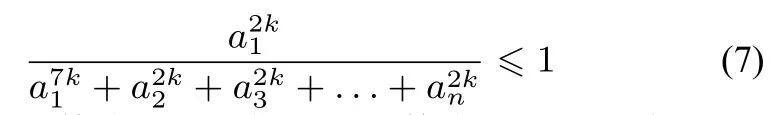
不等式(6)与不等式(7)相减,即得不等式(5)成立.当k=1时,不等式(4)成立.
3 问题2555 的拓展
3.1 问题2555 的拓展
定理3已知正实数a,b,c满足abc≥1,4q >p >q >0,则

3.2 问题2555 拓展的推广
定理4已知ai >0(i= 1,2,...,n,n≥3,n ∈N+),且≥1,(n+1)q >p >q >0,∑为对ai(i=1,2,...,n)循环求和,则
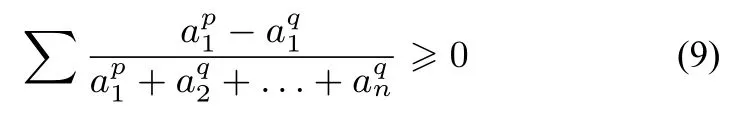
证明ai >0(i= 1,2,...,n,n≥ 3,n ∈N+), 且≥1, 不妨设a1≥a2≥...≥an >0, 由切比雪夫不等式和均值不等式,

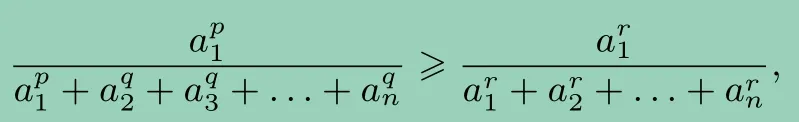
同理,
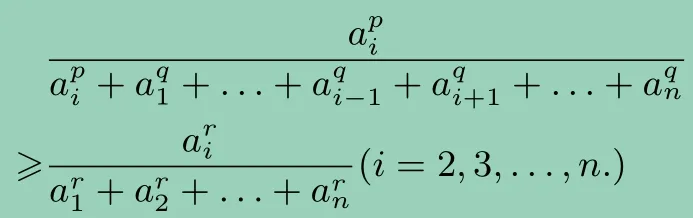
求和,得
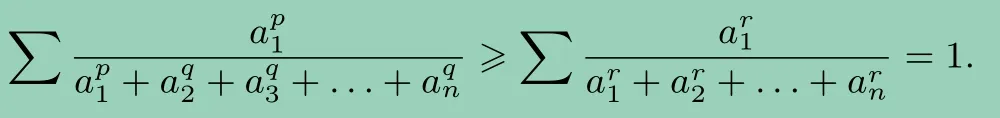
即
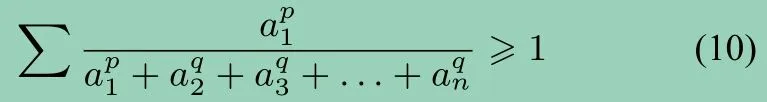
再由切比雪夫不等式和均值不等式,
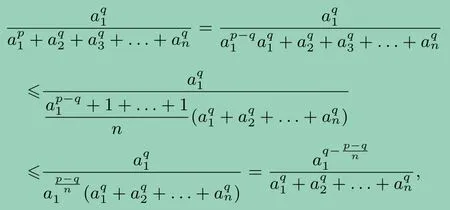

求和,得
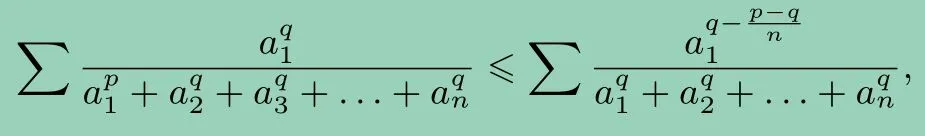
又q >q->0,由不等式(*),得
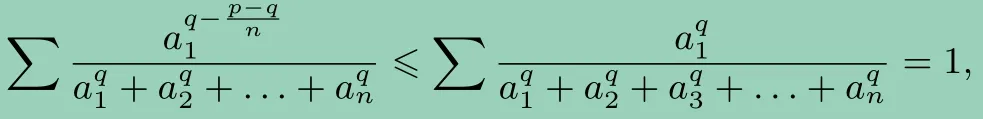
故

不等式(10) 与不等式(11) 相减, 即得不等式(9) 成立.当n=3 时,不等式(8)成立.
